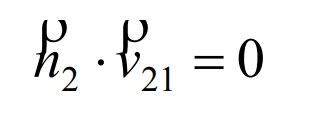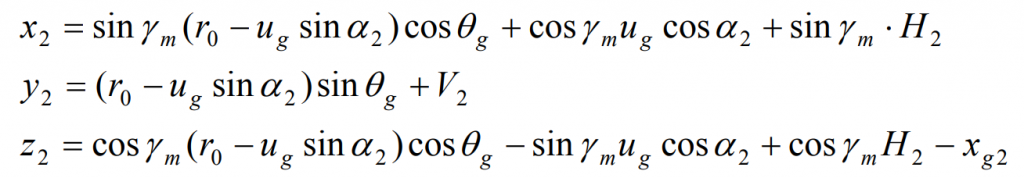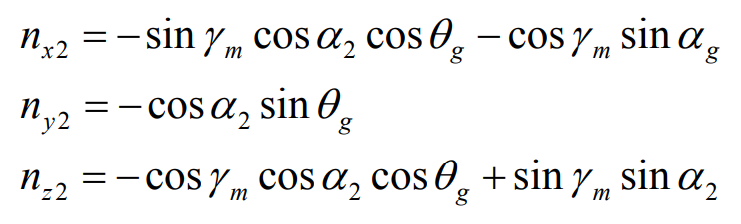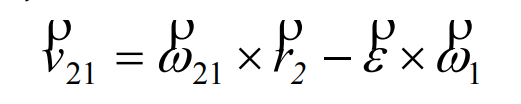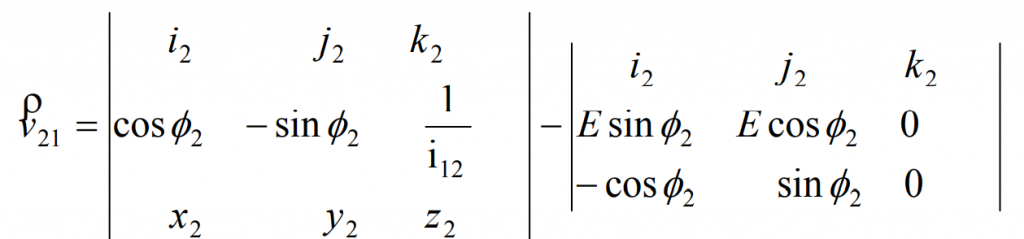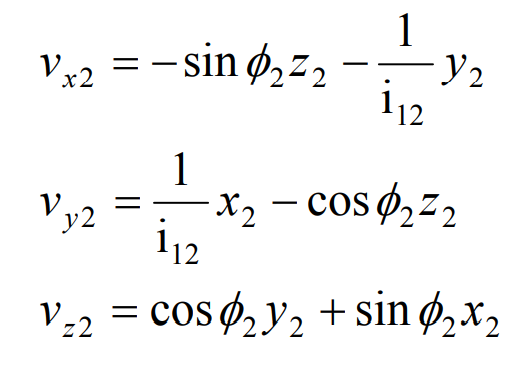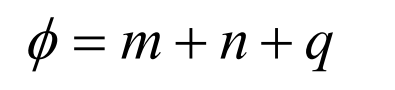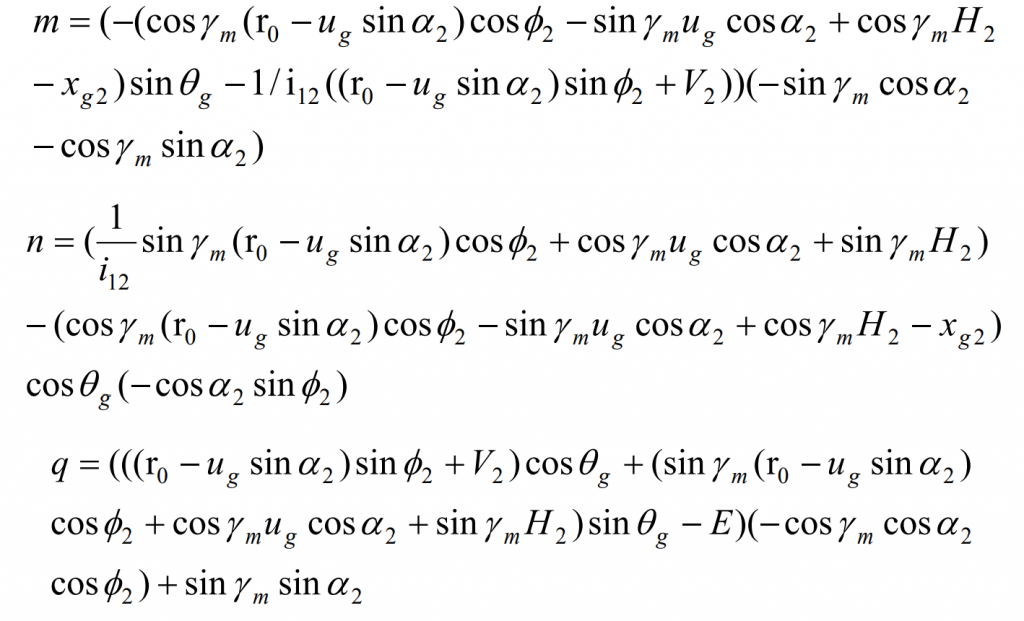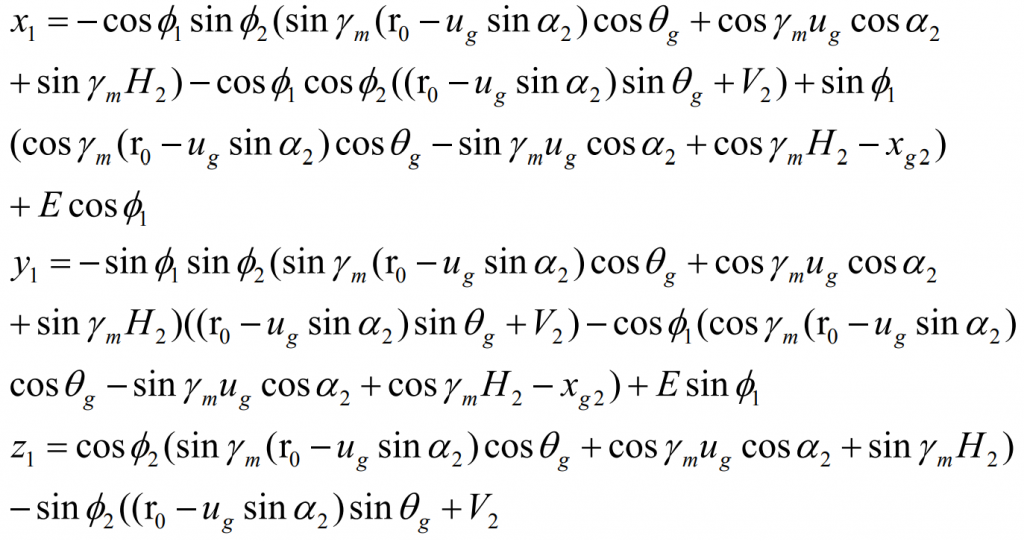In the process of envelope generation of hypoid gear pinion, there is a meshing relationship between hypoid gear wheel tooth surface and small gear tooth surface, that is, there is a meshing equation between them, that is:
Where, N2 – common normal vector; V21 – the relative movement speed of the big wheel and the small wheel of the tool in the envelope process.
The gear tooth surface of hypoid gear used in the enveloping process is the gear tooth surface calculated by the forming method mentioned above, so the tooth surface equation of tool big wheel is the same as that of big wheel, that is:
When machining the hypoid gear wheel by forming method, the common normal equation of the hypoid gear wheel is derived from the common normal of the hypoid gear wheel cutter. In the enveloping process of the hypoid gear pinion, because the hypoid gear wheel tooth surface is directly used to envelop the small gear tooth surface, their common normal equations are the same, that is:
Here, the subscript “2” indicates that its vector is represented in the coordinate system S2. Here R2 is the expression of the last line of the gear tooth surface equation of the hypoid gear.
Substitute the formula into:
Expand the right formula to obtain:
By sorting out the above formula, we can get the meshing equation of the large wheel enveloping the hypoid gear wheel with small number of teeth and large reduction ratio. The meshing equation is a meshing equation containing three parameters UG θ g、 Φ 2, namely:
Where:
The parameters can be eliminated by combining the above meshing equations Φ 2. In this way, the formula becomes a curved surface equation with two parameters, that is, the tooth surface equation R1 (UG, θ g) , i.e.: