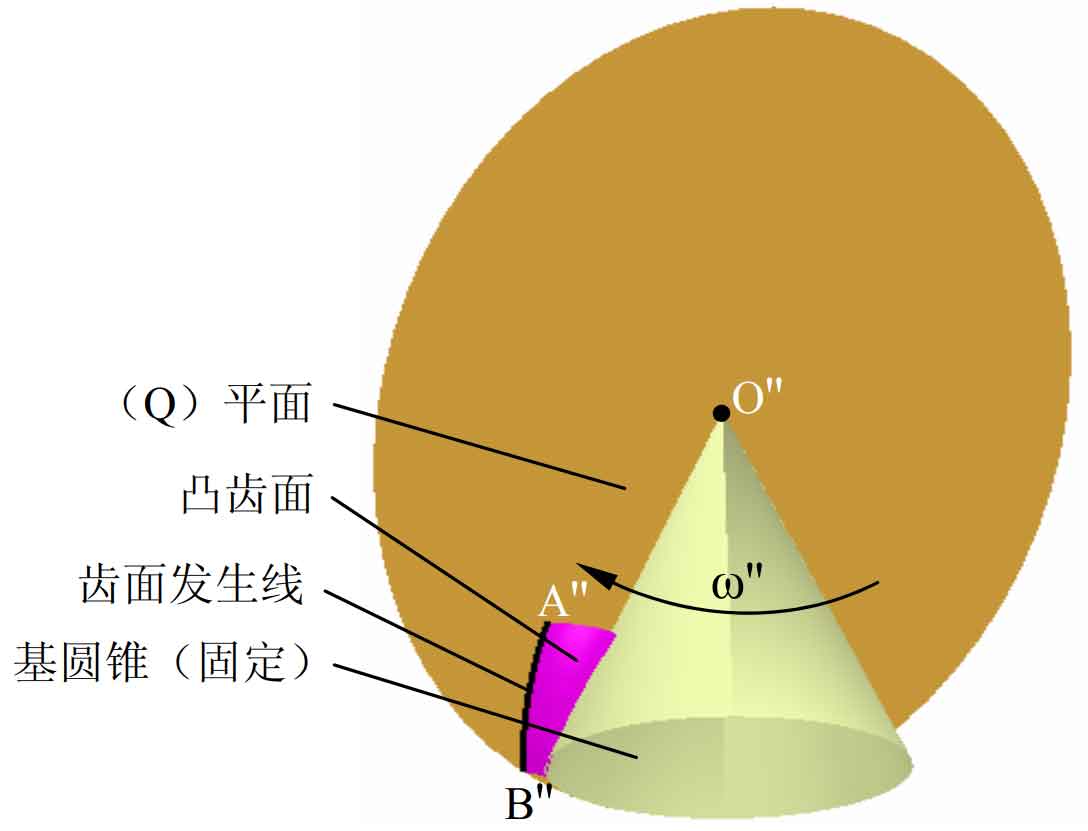
In order to intuitively analyze the generation principle of convex tooth surface of right-hand spiral bevel gear, the method of establishing concave tooth surface generation model is used, and the three-dimensional generation model of convex tooth surface of right-hand spiral bevel gear is established by comprehensively using the wireframe and surface design module, assembly design module and DMU kinematics module of CATIA software, as shown in Figure 1. (Q) The plane is tangent to the base cone, and the center of the (q) plane coincides with the vertex of the base cone at the o ” point. When the base cone is fixed, the (q) plane is ω” When the rotation speed is pure rolling on the base cone, the tooth surface occurrence line – a ”b’ ‘will pure roll on the base cone with the (q) plane, so as to generate the convex tooth surface of the right-hand spiral bevel gear. The whole generation process of convex tooth surface is that the tooth surface generation line is gradually wound on the base cone from a ” at the small end to B ” at the large end, and the convex tooth surface model is generated from the base cone to the face cone.
By comparing the generation process of concave tooth surface and convex tooth surface of right-hand spiral bevel gear, there are the following differences: ① the concave tooth surface is wound on the base cone from the generation line of tooth surface from the big end to the small end; The convex tooth surface is just the opposite, winding from the small end to the large end; ② When the base cone is fixed, the pure rolling direction of the (q) plane on the base cone is opposite. The same points are as follows: ① both convex and concave tooth surfaces are generated by expanding the tooth surface generation line from the base cone to the face cone; ② The center of the (q) plane coincides with the cone top of the base cone, and the (q) plane always maintains a tangent relationship with the base cone, and carries out pure rolling motion to generate the tooth surface of spiral bevel gear.
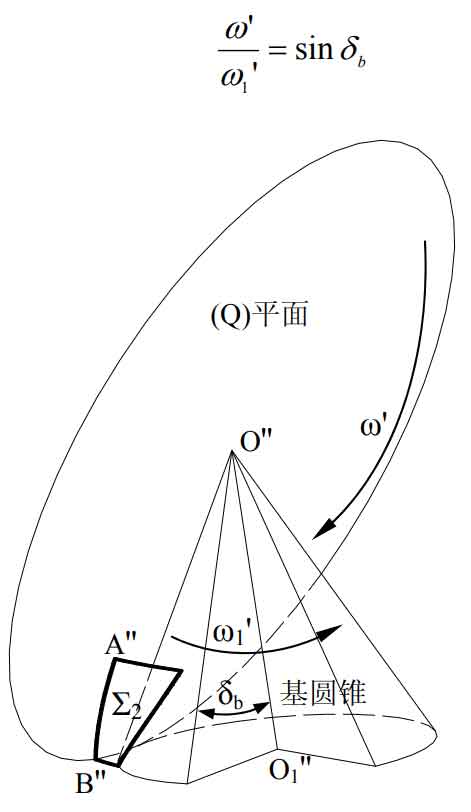
Using the same analysis method as the concave tooth surface, the spatial rotation motion of the (q) plane on the base cone in the process of generating the convex tooth surface is decomposed into two plane rotation motions, as shown in Fig. 2. (Q) The plane is tangent to the base cone, and the center of the (q) plane coincides with the top of the base cone at the o ” point. When the (q) plane and the base cone rotate at an angular velocity around their own geometric axis respectively ω’ And ω When 1 ‘rotates, the generating line of the tooth surface of the (q) plane – the arc segment a”b ” will roll purely on the base cone, and the spatial motion track of the arc segment a ”b’ ‘relative to the base cone is the convex tooth surface of the right-hand spiral bevel gear. Based on the motion analysis of the generation process of concave tooth surface, in order to ensure the pure rolling relationship between (q) plane and base cone, ω’ And ω 1 ‘must satisfy the following relation:
By comparing and analyzing the rotation motion of the base cone and the (q) plane required in the generation process of the convex and concave tooth surfaces of the right-hand spiral bevel gear, the following conclusions are drawn: ① whether it is the generation motion of the convex tooth surface or the concave tooth surface, the rotation speed direction of the base cone is opposite to that of the (q) plane, and the two speeds are related to the sinusoidal value of the base cone angle; ② The rotation direction of the generated convex tooth surface is opposite to that of the generated concave tooth surface, that is, the rotation direction of the generated convex tooth surface is opposite to that of the generated concave tooth surface.