Figure 1 shows the influence curve of friction on the second-order superharmonic resonance. With the increase of friction, the vibration response amplitude decreases significantly, and the vibration response amplitude decreases by 16% when the friction coefficient is from 0.1 to 0.2. It can be seen that the tooth friction can effectively reduce the vibration response amplitude.
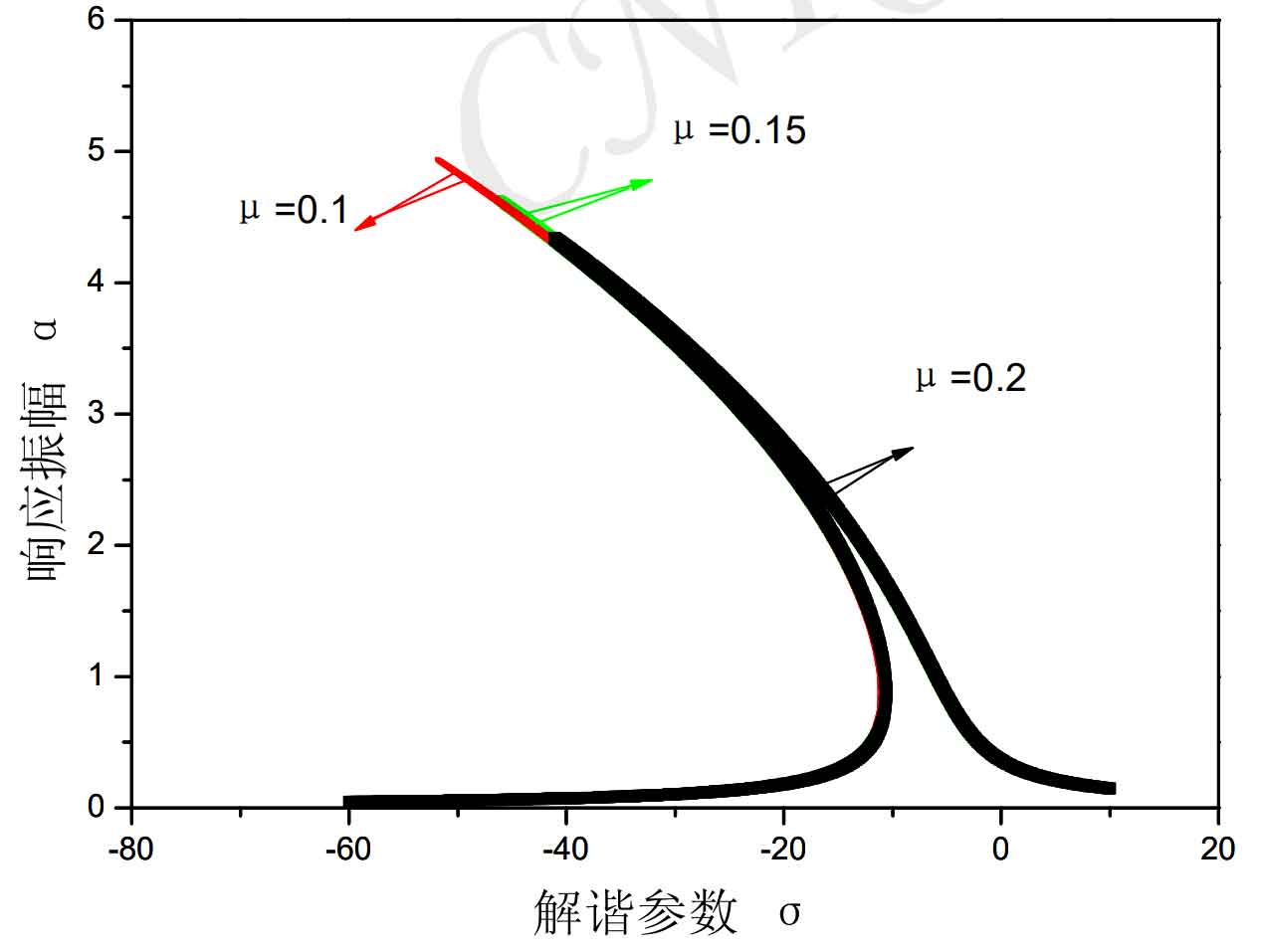
Figure 2 shows the influence curve of static load on the second-order superharmonic resonance. It can be seen that when considering the tooth friction, the vibration response amplitude decreases with the static load, and the resonance response amplitude decreases significantly. When the static load is 0.3, 0.5 and 0.8, the amplitude of vibration response decreases by 24%, 22.8% and 12% respectively, and the resonance frequency also tends to increase, but the trend is small and not obvious.
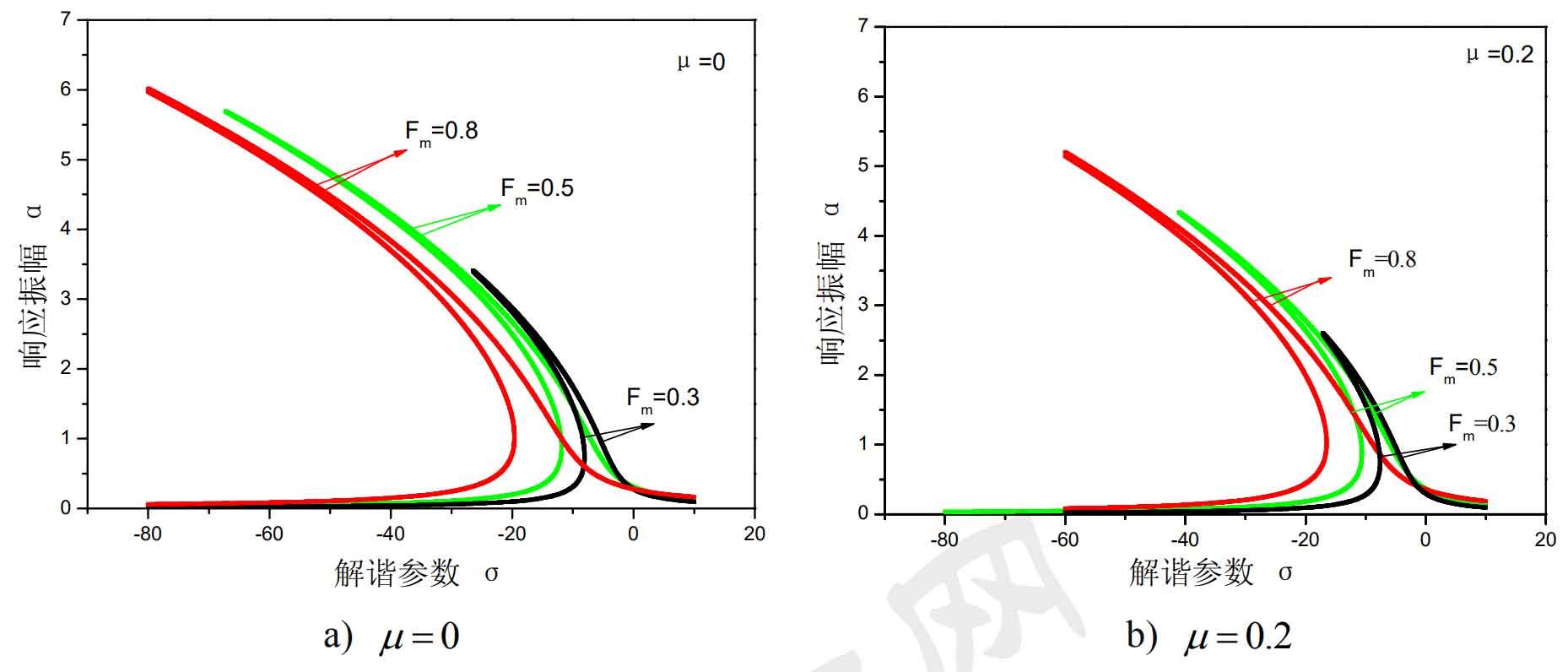
Figure 3 shows the influence curve of dynamic load on the second-order superharmonic resonance. When considering the tooth friction, the vibration response amplitude decreases significantly with the decrease of dynamic load. When the dynamic load is 0.3, 0.5 and 0.8, the amplitude of vibration response decreases by 23.8%, 21.4% and 11.6% respectively. It can be seen that the smaller the dynamic load is, the more obvious the tooth friction reduces the amplitude of vibration response, but the tooth friction basically has no effect on the resonance frequency.
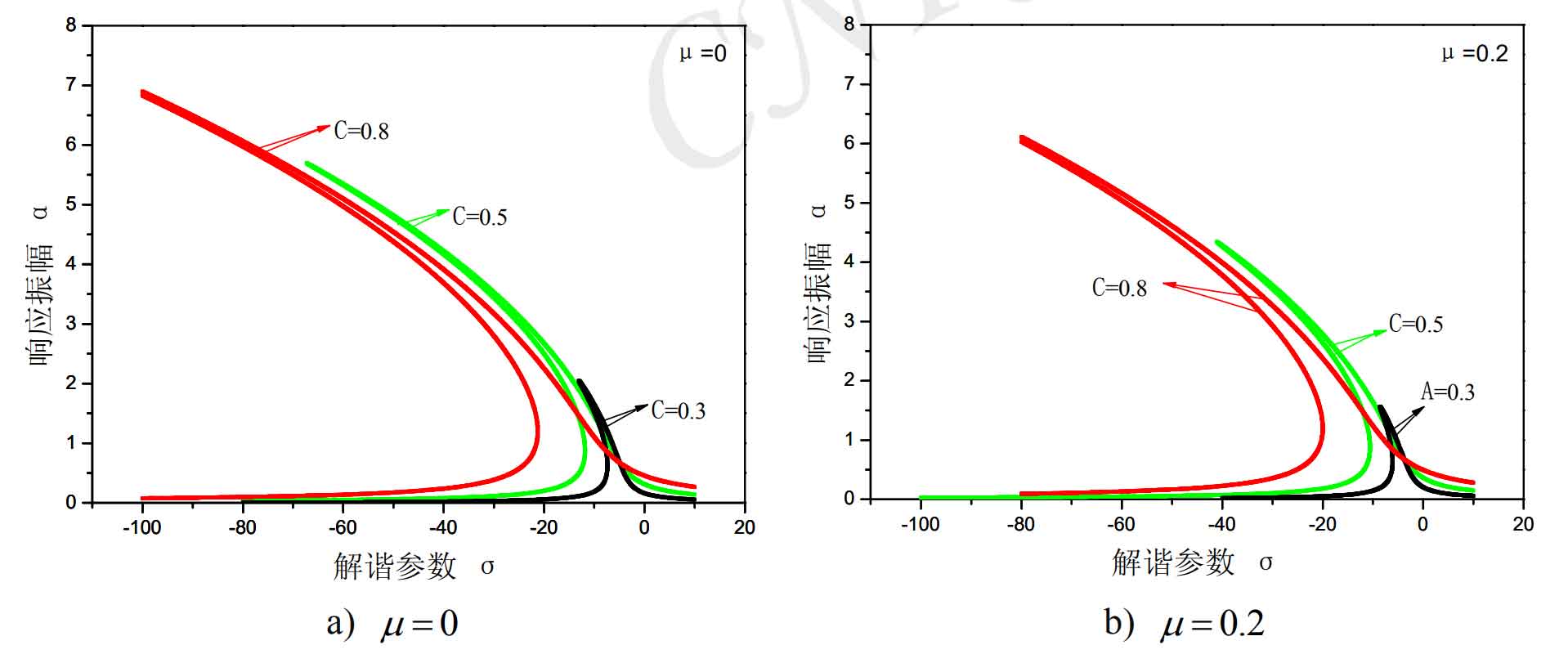
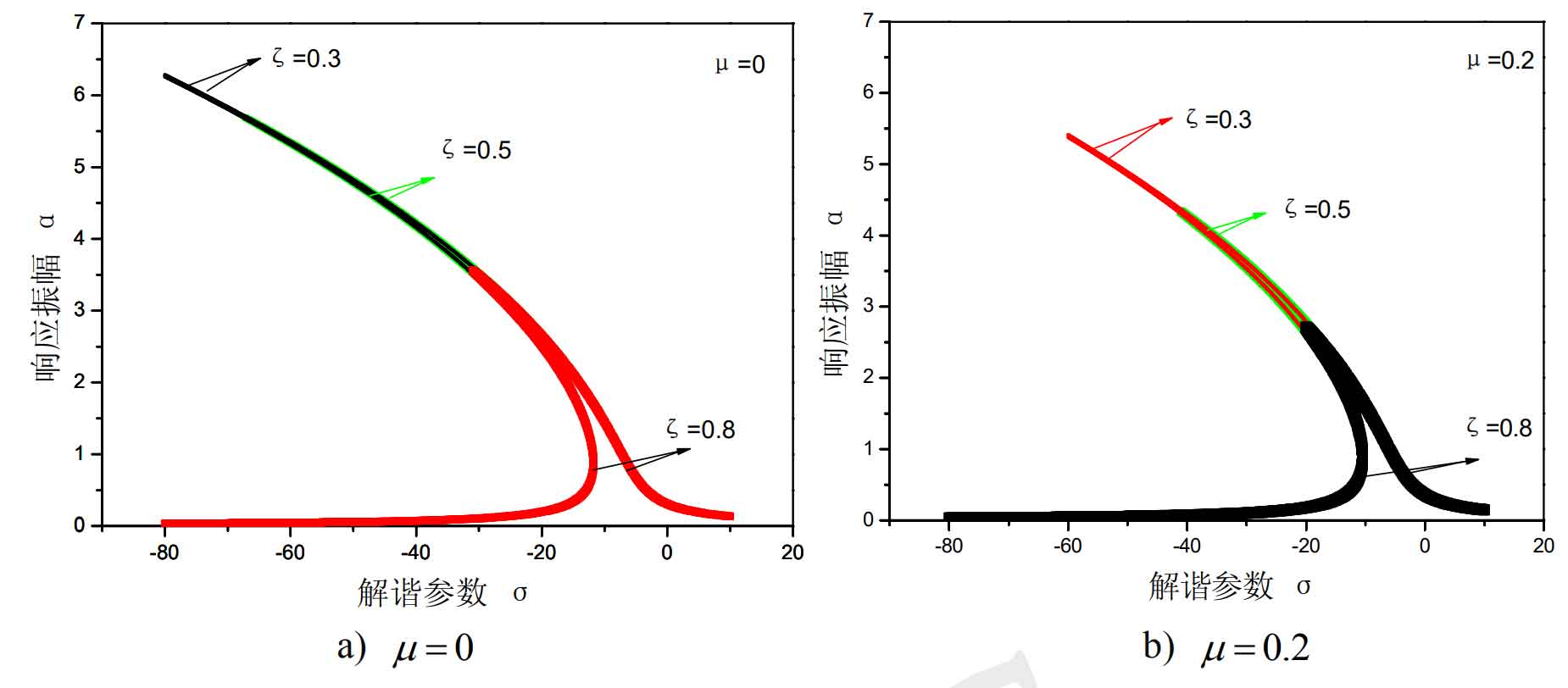
Figure 4 shows the influence curve of damping on the second-order superharmonic resonance. Damping has an obvious inhibitory effect on the amplitude of the second-order superharmonic resonance. When the damping is 0.3, 0.5 and 0.8, the amplitude of response vibration amplitude decreases by 12.6%, 22.8% and 27.8% respectively. It can be seen that the amplitude of tooth friction on resonance response decreases more obviously with the increase of damping.