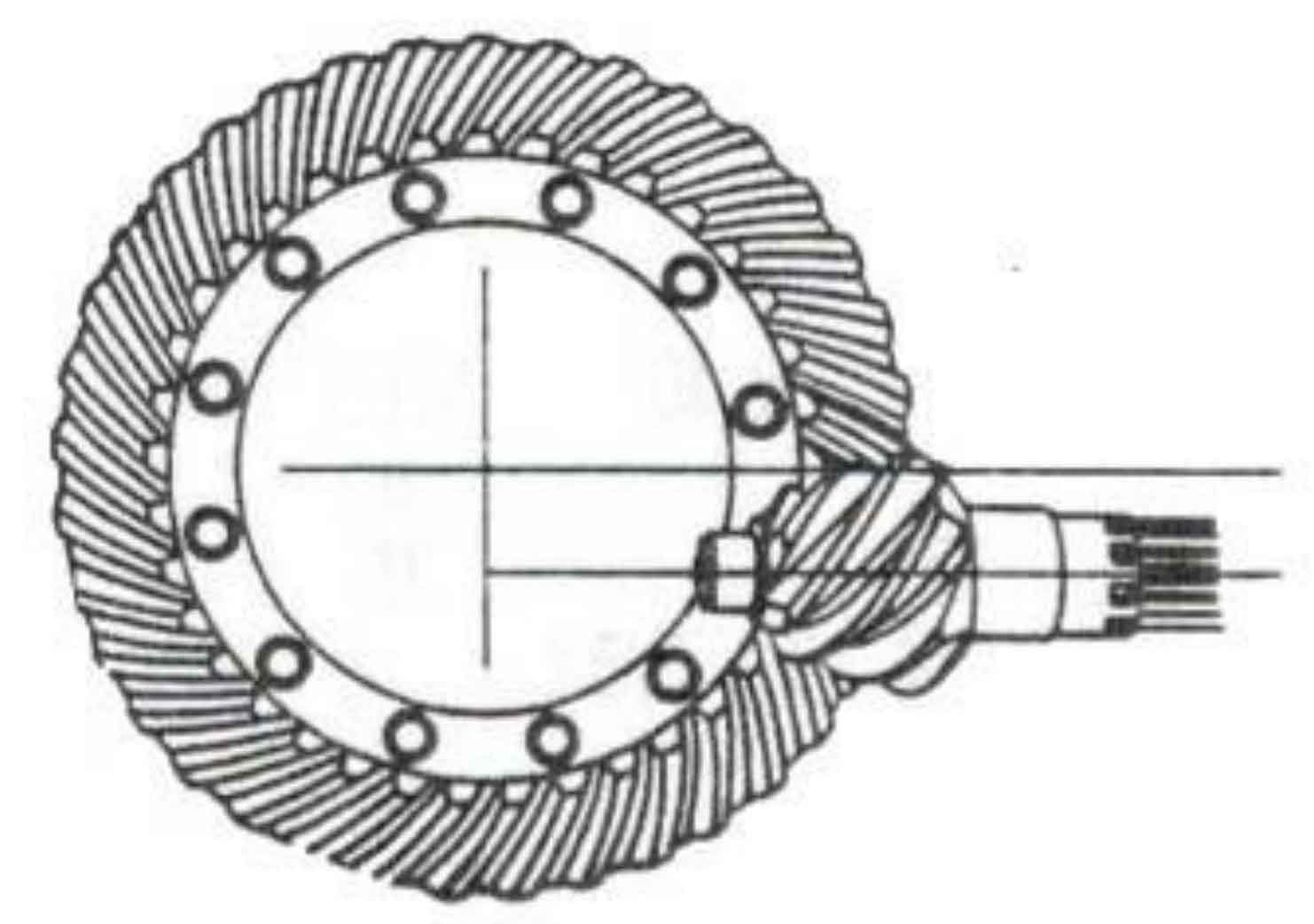
The geometric model of drive axle hypoid gear is the basis of gear contact, transmission error, load and other analysis. First, it is necessary to establish an accurate geometric model of hypoid gear tooth surface. With the change of the machining method of hypoid gears, the geometric modeling method of gears also changes greatly.
Abroad, in 1993, Fong Z H et al. Established a geometric calculation model of hypoid gear tooth surface based on the quasi double curved surface geometric mathematical model proposed by Litvin. In 2000, Fong z.h. et al. Summarized different machine tool machining methods and proposed a general geometric modeling method for hypoid gears. In the same year, Vimercati, M A method to accurately represent the machining of hypoid gears by the end face hobbing method (FH) is proposed. In this model, the real machining process of gears and the precise tool shape are considered. Due to the dynamic effect of machine tool, gear processing temperature, gear heat treatment and other factors, the machined tooth surface may deviate from the theoretical geometric tooth surface. Many papers focus on minimizing tooth surface deviation by adjusting machine tool parameters. Some of the literatures establish algorithms to determine the theoretical design parameters of machine tools by measuring the discrete coordinates of tooth surfaces. There are also some literatures that first measure the deviation between the machined tooth surface geometry and the theoretical tooth surface at the determined point, and then add the theoretical tooth surface and the machining deviation of the tooth surface to represent the real tooth surface.
In China, because spiral bevel gears or hypoid gears are widely used in key fields of aviation, aerospace, automotive and other industries, many scholars have done in-depth research on the design, processing and optimization of such gears. As early as 1988, in order to reveal the inherent principles of many calculation cards in the gear processing process of Gleason machine tool, Zheng Changqi and others used the principle of differential geometry to systematically analyze the machining parameters of hypoid gears, which laid the foundation for the research on the machining principle of hypoid gears in China. Subsequently, many scholars have conducted a comprehensive study on the machining and manufacturing process of hypoid gears. In the aspect of hypoid gear tooth surface modeling, in recent years, Wang Yuqing, Tang Jinyuan, Uranus, mingxijun and others have studied the mathematical model in the machining of spiral bevel gears. According to the principle of hypoid gear tooth surface generation proposed by litivin, the tooth surface equation of large and small gears is derived by simulating the tool path, the accurate mathematical model of the theoretical tooth surface points of hypoid gears is obtained, and the gear tooth surface points are obtained by using numerical calculation software.
To sum up, there are the following deficiencies in the establishment of these models: first, the established model is different from the actual machine tool structure, and the current model does not give a detailed direct correlation with the actual machine tool structure. Second, there are deficiencies in the solution of the model. Because the coordinate equation of hypoid gear tooth surface is a nonlinear equation, the solution of the nonlinear equation is related to the initial value, and the current literature does not give the value method of the initial value and the solution method. Based on the geometric model of hypoid gear tooth surface proposed by litivin, a general method for solving the three-dimensional geometry of hypoid gear tooth surface is established, which lays the foundation for the subsequent analysis of drive axle hypoid gear.