Select a spur gear to calculate its stiffness. The reason why spur gear is selected as the research object is that there are widely used empirical formulas for the calculation method of meshing stiffness of spur gear, and the calculation results can be compared. Moreover, the above calculation method of meshing stiffness is also applicable to spur gear. Therefore, the accuracy of the above calculation method can be verified through the calculation of the stiffness of spur gear. The parameters of spur gear are shown in the table.
| Parameters | Wheel | Pionion |
| Number of teeth | 34 | 34 |
| Pressure angle | 20 | 20 |
| Modulus | 2.5 | 2.2 |
| Displacement coefficient | 0 | 0 |
| Tooth surface width | 12 | 12 |
| Fillet radius of tool tip | 0.44 | 0.44 |
| Elastic modulus | 210 | 210 |
| Poisson’s ratio | 0.3 | 0.3 |
| Input torque | 5000 | 5000 |
| Input speed | 3000 | 3000 |
The finite element model is established according to the parameters of the spur gear, and the meshing stiffness of the spur gear is obtained by using the meshing stiffness calculation method of the spur gear. The finite element calculation results are shown in figure (a) and the meshing stiffness results of the spur gear are shown in figure (b).
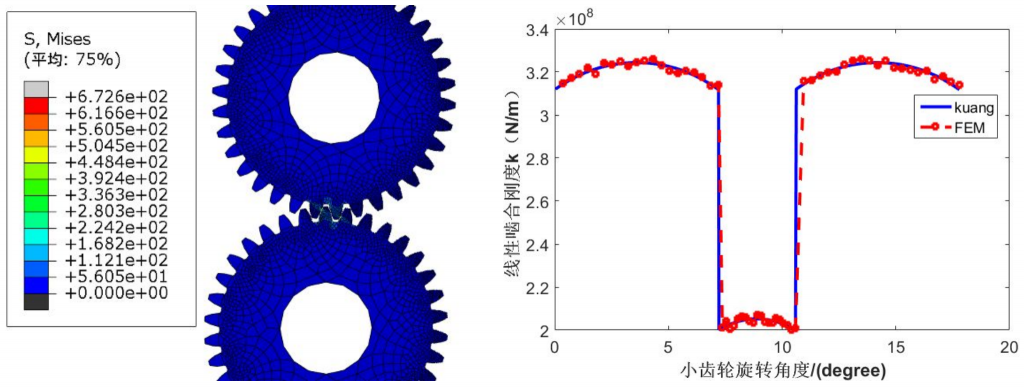
It can be seen from the figure that the meshing stiffness of spur gear calculated by this method is basically the same as that calculated by Kuang method. The influence of contact nonlinearity and friction nonlinearity of spur gear is taken into account in the finite element method, resulting in fluctuations in the calculation results. The sudden change of spur gear from double tooth meshing to single tooth meshing makes the meshing stiffness of spur gear sudden change, Therefore, large meshing impact noise will occur in the meshing process of spur gears.
