Input the obtained time-varying meshing stiffness curve into the dynamic equations, obtain the vibration response of single-stage helical gear transmission under three working conditions of input torque of 80N · m, 100N · m and 120N · m, and draw the vibration speed diagram as shown in Figure 1.
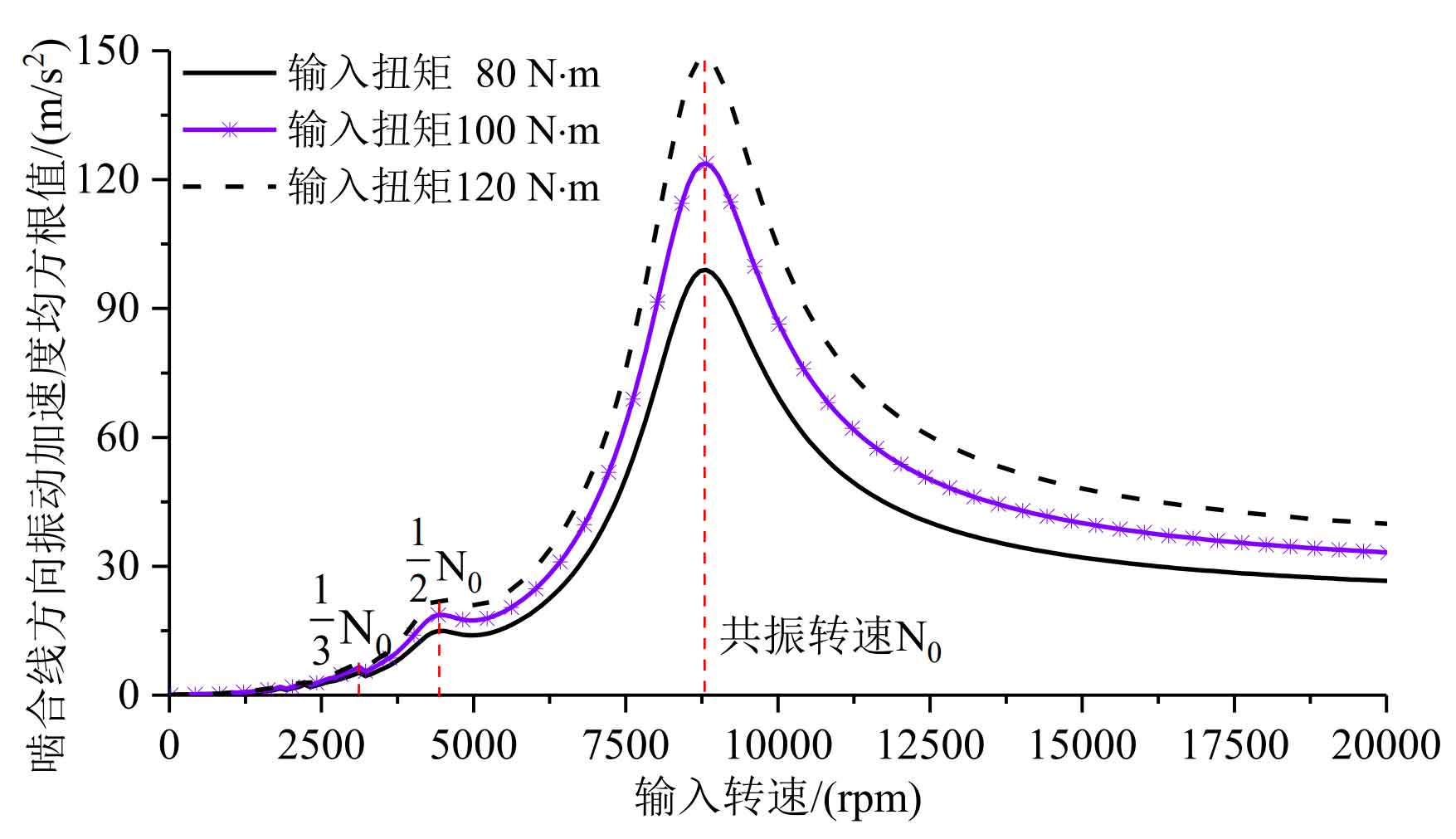
It can be seen from Fig. 1 that obvious super harmonic resonance occurs at 1/3 and 1/2 resonant speed N0; The vibration acceleration of helical gear increases with the increase of load; In the non resonant region, the root mean square acceleration of helical gears does not always increase with the increase of the speed, but has a slight downward trend after passing the resonant region. That is to say, when only time-varying meshing stiffness excitation is considered, in the over resonance region, the effect of speed increase on the vibration characteristics of the system is not significant.
This phenomenon is due to that time-varying meshing stiffness is a parametric excitation form, which is reflected in the dynamic model as the change of time-varying coefficient of elastic force term (i.e. helical gear meshing force), and its mean value and amplitude have no essential relationship with the speed. The vibration generated by the system under parametric excitation is parametric vibration, and there is no external force input except the driving force. The vibration of such system is caused by the periodic change of the internal parameters (meshing stiffness) of the system. When the rotational speed rises to the resonance region, the excitation frequency of the parameter is gradually far away from the resonance frequency of the system, and the influence of the change of the parameter on the system is also reduced. Therefore, the system vibration does not always increase with the increase of rotating speed.
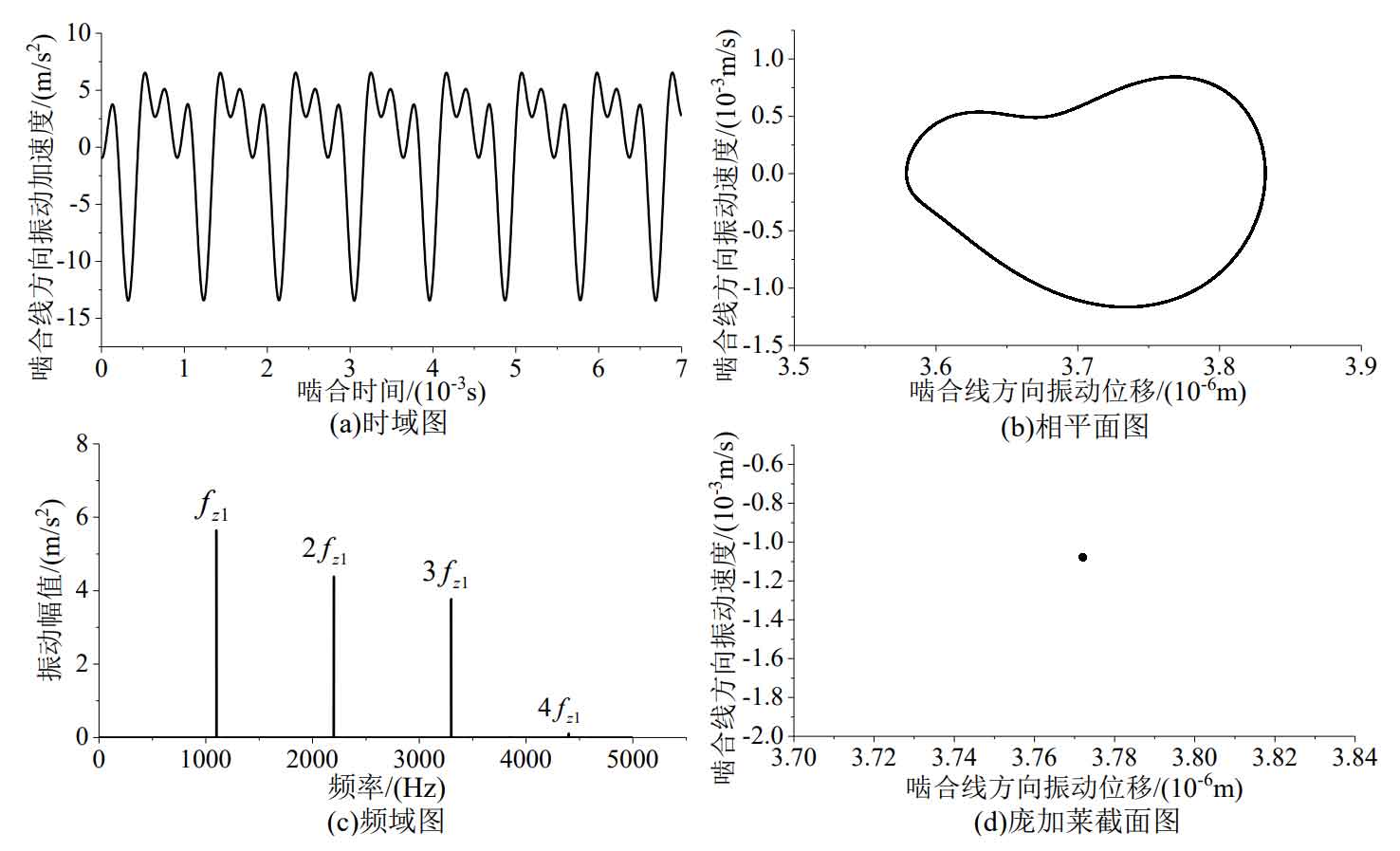
In order to analyze the vibration characteristics of single-stage high-speed helical gear transmission, the vibration responses of single-stage helical gear transmission under the excitation of time-varying meshing stiffness at three different speeds are respectively made, as shown in Figures 2 to 4. In the figure, fz1 represents the tooth frequency of the input tooth pair.
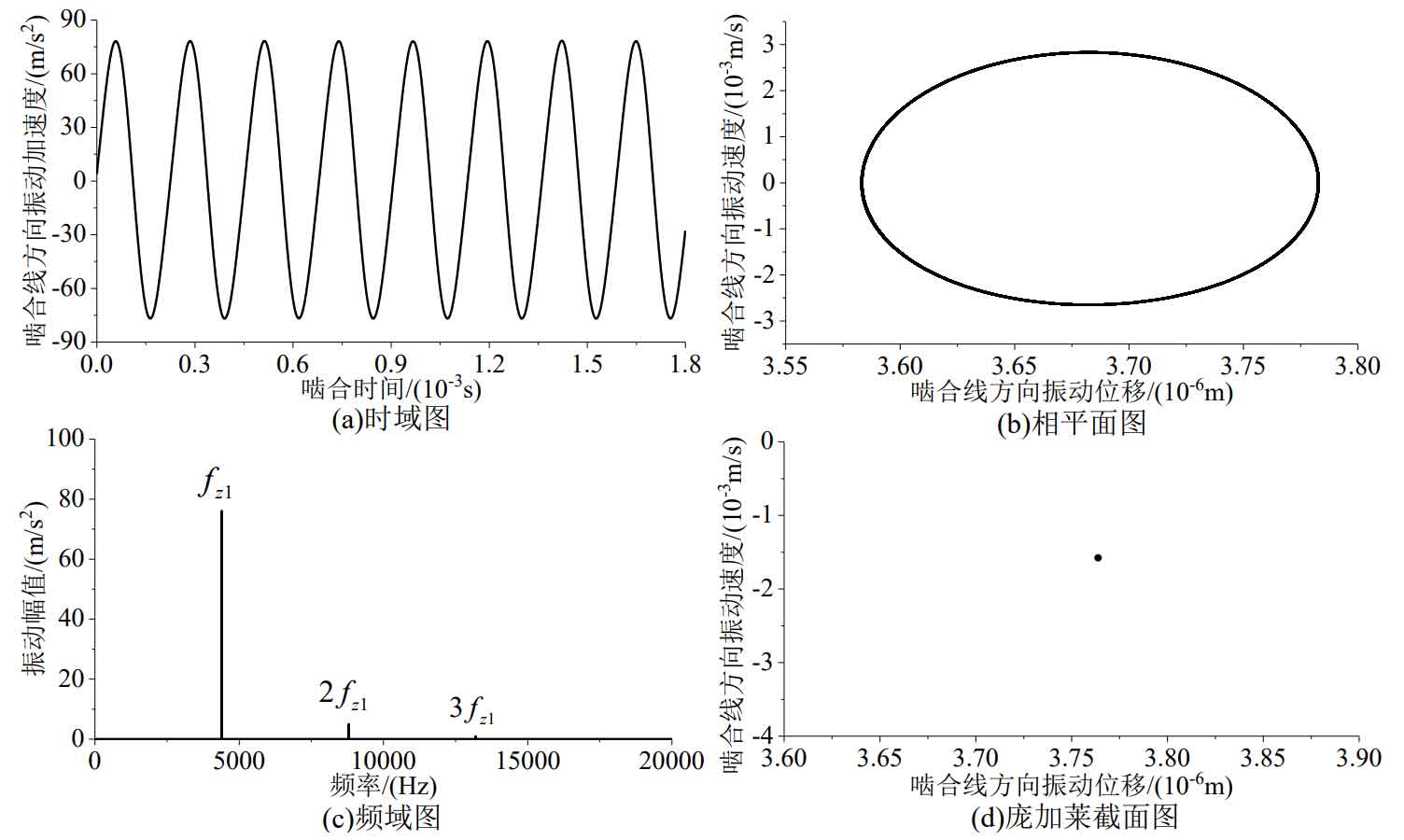
Figure 2 and Figure 3 show the vibration response of single-stage helical gear transmission at 3000 rpm and 6000 rpm. It can be seen from the figure that under the excitation of time-varying meshing stiffness alone, the phase diagram of single-stage helical gear transmission is a closed curve, and its Poincare section diagram is a single point, so the vibration response is obviously periodic. And the system response frequency only includes the tooth frequency and its double frequency, and the frequency component is very simple. The frequency domain response of the system in the figure shows that the amplitude of one time tooth frequency is the highest among all response frequencies. This is due to the maximum amplitude of one time of the tooth frequency in the excitation frequency, while the other excitation frequencies are smaller. In addition, in the vibration response, the amplitude of twice the tooth frequency is also large. This is because at 3000 rpm and 6000 rpm, the natural frequency of the system is between the double tooth frequency and the double tooth frequency. At this time, the natural frequency of the system is also close to the double tooth frequency, so the response amplitude is high.
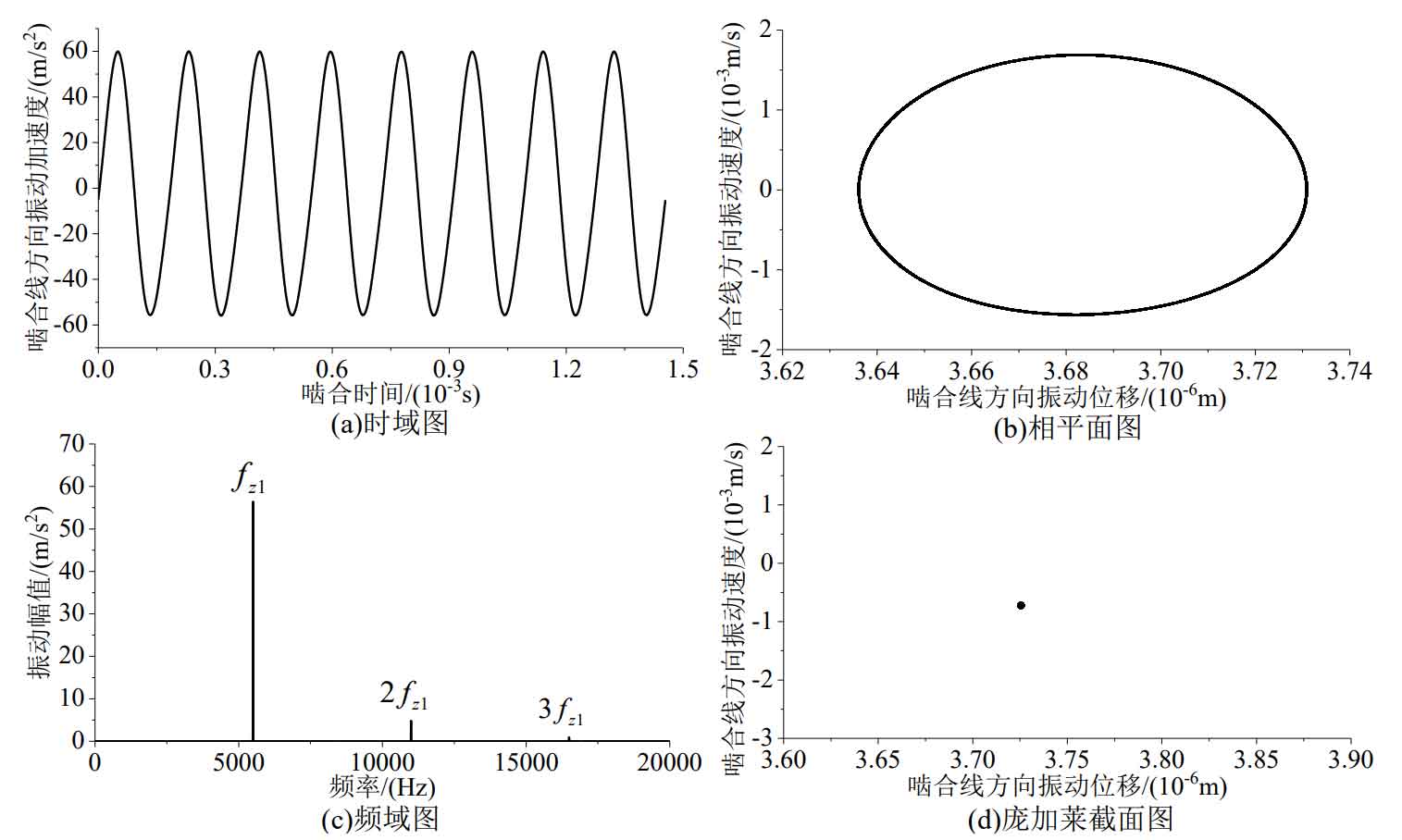
Figure 4 shows the vibration response of single-stage helical gear transmission at 15000 rpm, which is consistent with the phenomena in Figure 2 and Figure 3. The difference is that the response frequency of the 15000 rpm system is smaller except for one time of the tooth frequency. This is because the double tooth frequency is greater than the natural frequency of the system, and other response frequencies are far away from the natural frequency of the system.
