According to the principle of gear engagement, the mathematical model of the planetary gear internal gear profile can be described as:
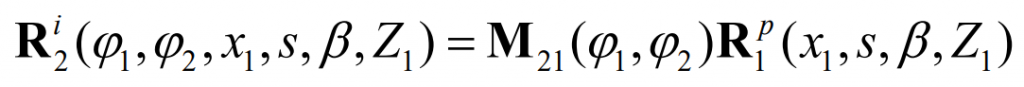
In which, Ri2( ϕ 1, ϕ 2,X1,s, β, Z1) is the envelope curve family formed in the meshing process of planetary gear external gear, M21( ϕ 1, ϕ 2) It is the coordinate transformation matrix from the coordinate system 1S to 2S, and the expression is as follows:
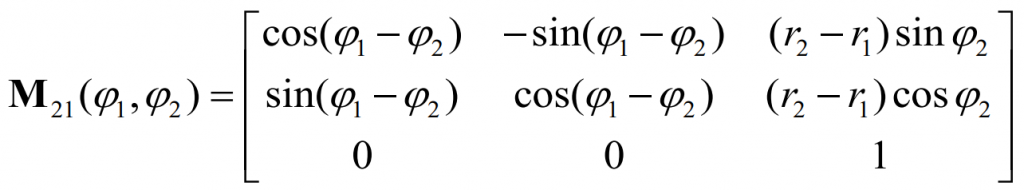
Similarly, considering the necessary conditions for the existence of envelope curve family, it is necessary to meet:
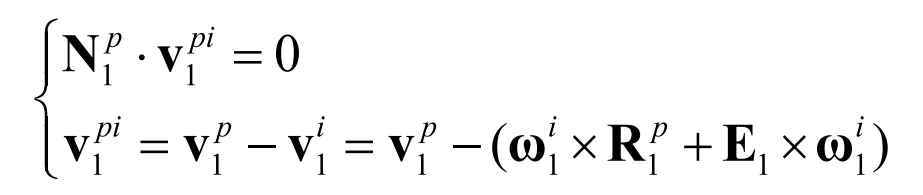
Where V1 ^ pi is the relative speed of the internal and external planetary gears in the coordinate system S1, V1 ^ i is the speed vector of the internal planetary gears, ω 1 ^ i is the angular velocity vector of the internal gear of the planetary gear, and E1 is the position vector from O1 to O2. The relationship between the three is as follows:
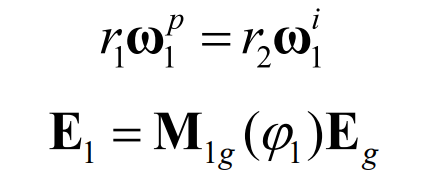
Where, M1g( ϕ 1) is the transformation matrix from the coordinate system S1 to Sg, and Eg is the position vector from O1 to O2 in the coordinate system Sg. The expressions are:
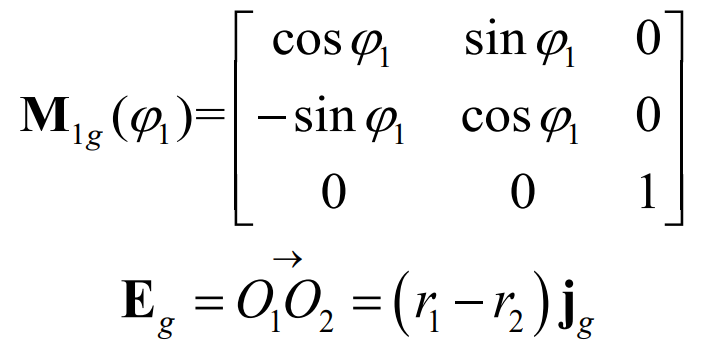
The simultaneous equation calculation results in:
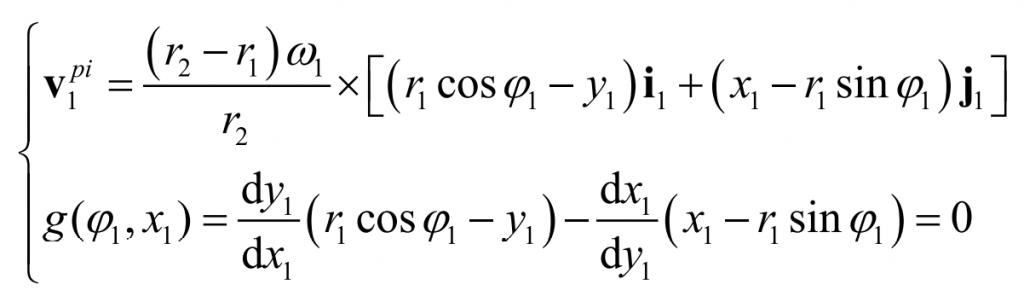
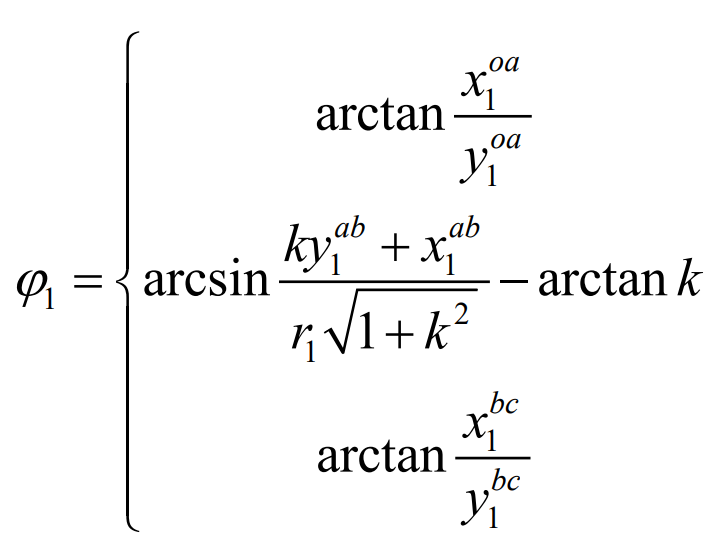
The parameters in the mathematical model of planetary internal gear tooth profile are obtained through calculation ϕ1 Functional relationship between x1:
The mathematical model of planetary internal gear profile can be obtained by substituting the equations in turn.
