The meshing solid model of helical gear is established in ANSYS, and the mesh of helical gear is divided and solved according to the general conclusion of mesh control in the contact area obtained from the normal contact simulation analysis of two elastic cylinders. The results of the solution are compared with the analytical solution to verify the validity of the conclusion in the contact simulation of helical gear.
In the design of helical gears, the maximum Hertz contact pressure during helical gear meshing is the basic parameter used for the evaluation of tooth contact fatigue strength. The calculation formula is as follows:
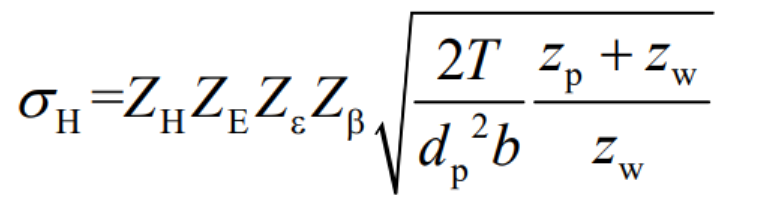
Where: σ H is the maximum Hertz contact pressure of helical gear; ZH is the regional coefficient; ZE is the elastic coefficient; Z ε Is the coincidence coefficient; Z β Is the helix angle coefficient; T is the transmission torque; DP is the diameter of the indexing circle of the pinion in the helical gear pair; B is the effective tooth width, Zp and Zw are the number of teeth of helical gear pair.
In order to calculate the half-width of the helical gear contact belt, the tooth surface contact can be regarded as two elastic cylindrical contacts. It can be deduced from the formula that the calculation formula of the half-width bg of the helical gear contact belt is:
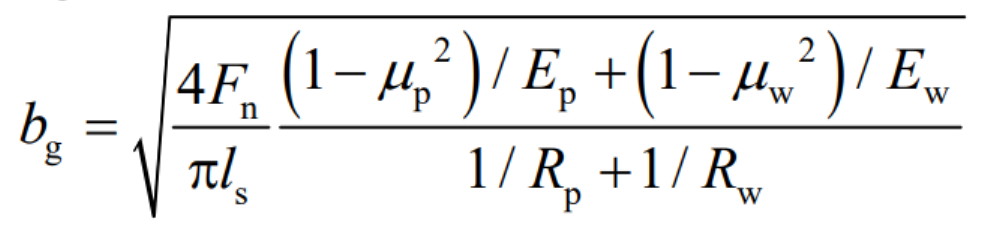
Where: Ep and Ew are the elastic modulus of helical gear pair, μ p、 μ W is the Poisson’s ratio of the helical gear pair, Fn is the normal calculated load of the helical gear pair, sl is the total length of the contact line, and d, wb d are the base circle diameter of the helical gear pair.
