The roughness model analyzes the tooth surface areas of five spiral bevel gears, predicts the surface roughness, and generates the surface morphology and roughness profile of these five areas. Therefore, different roughness along the tool feed direction XW can be predicted. Different tool side number (N) t and feed value (f) are simulated. The tooth surface roughness value of each spiral bevel gear depends on the machining type, cutting mode and programming height display. These values also depend on the tooth surface (concave or convex) and the analyzed area 1 to 5. This is the result of Grissom’s method, which produces a spiral bevel gear and a variable spiral bevel gear height.
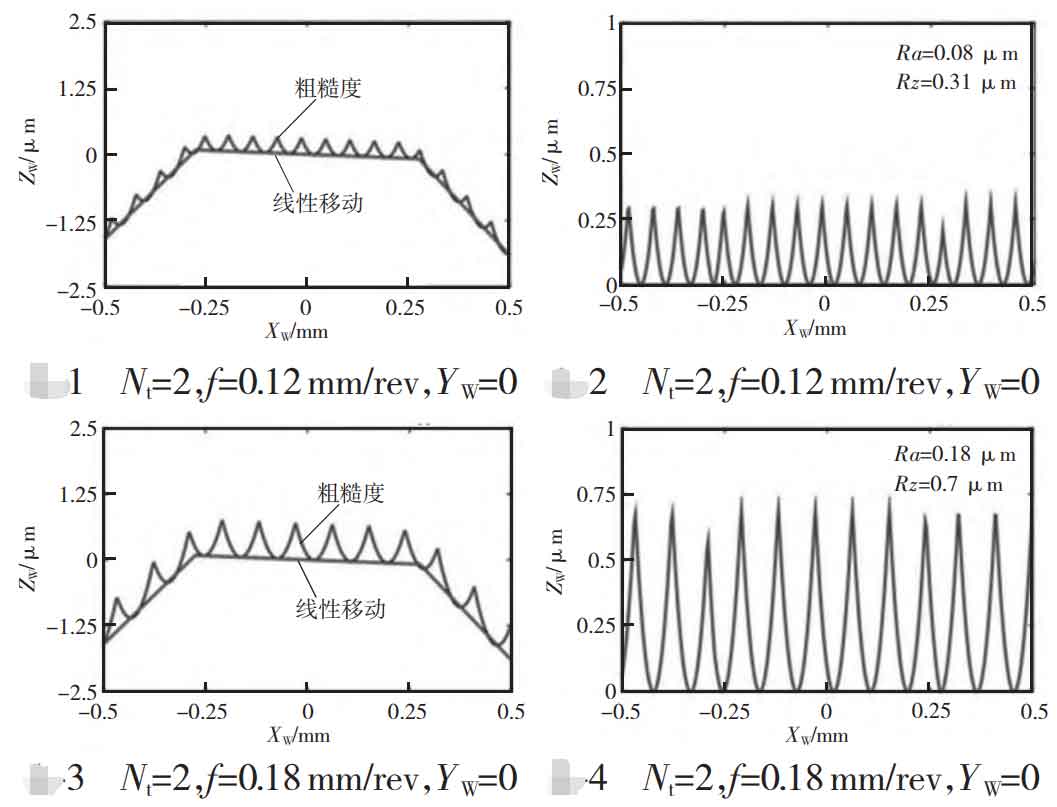
Therefore, the roughness value obtained is higher in the area closest to the outer diameter. The shape of the roughness profile is the result of the linear segment between two machining programs (interpolation points) that define the tool path. The distance between different interpolation points in the same path is about 0.56 mm. In Figure 1 and Figure 3 on the next page, it can be seen that the roughness profile depends on the number of tool edges (N) t and the program tool feed value (f). In Figure 2 and Figure 4 on the next page, the shapes related to the spiral bevel gear components are eliminated. For each roughness profile, the average roughness parameter Ra and the average roughness parameter Rz of the algorithm are obtained.
Spiral bevel gear processing in multi-task machines has flexibility, size and various geometric shapes, and can be processed in this type of machine. It is proposed as a practical application of this type of technology. The geometry of spiral bevel gear is a complex geometry, which can be processed with 3+2 axis kinematics. The rotation axis can be positioned and fixed from a more robust process. In this case, the obtained surface roughness value is acceptable. In addition, the processing cost of 3+2 is lower because there are fewer interpolation axes required. In addition, 3+2-axis programming is not as challenging as 5-axis programming. This work verifies the established surface morphology model of ball mill, and the experimental value is in good agreement with the theoretical value. In addition, the calculation results of different programming steps maintain the same trend. After programming each finishing strategy, terrain simulation becomes an indispensable tool, because it can optimize the processing results without using trial and error method, thus reducing the cost and time.
