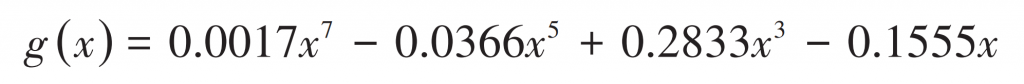Generally speaking, the coincidence degree of the helical gear system is greater than 2, and the continuous gradual involution of its meshing process makes the process of meshing in and out of the helical gear more stable than that of the spur gear system. However, if the segmented clearance function g (x) is used, the analysis result is greatly different from the engineering practice, so it is necessary to polynomial fit the clearance function g (x). The corresponding coefficients of polynomial fitting under different orders are given in the table below.
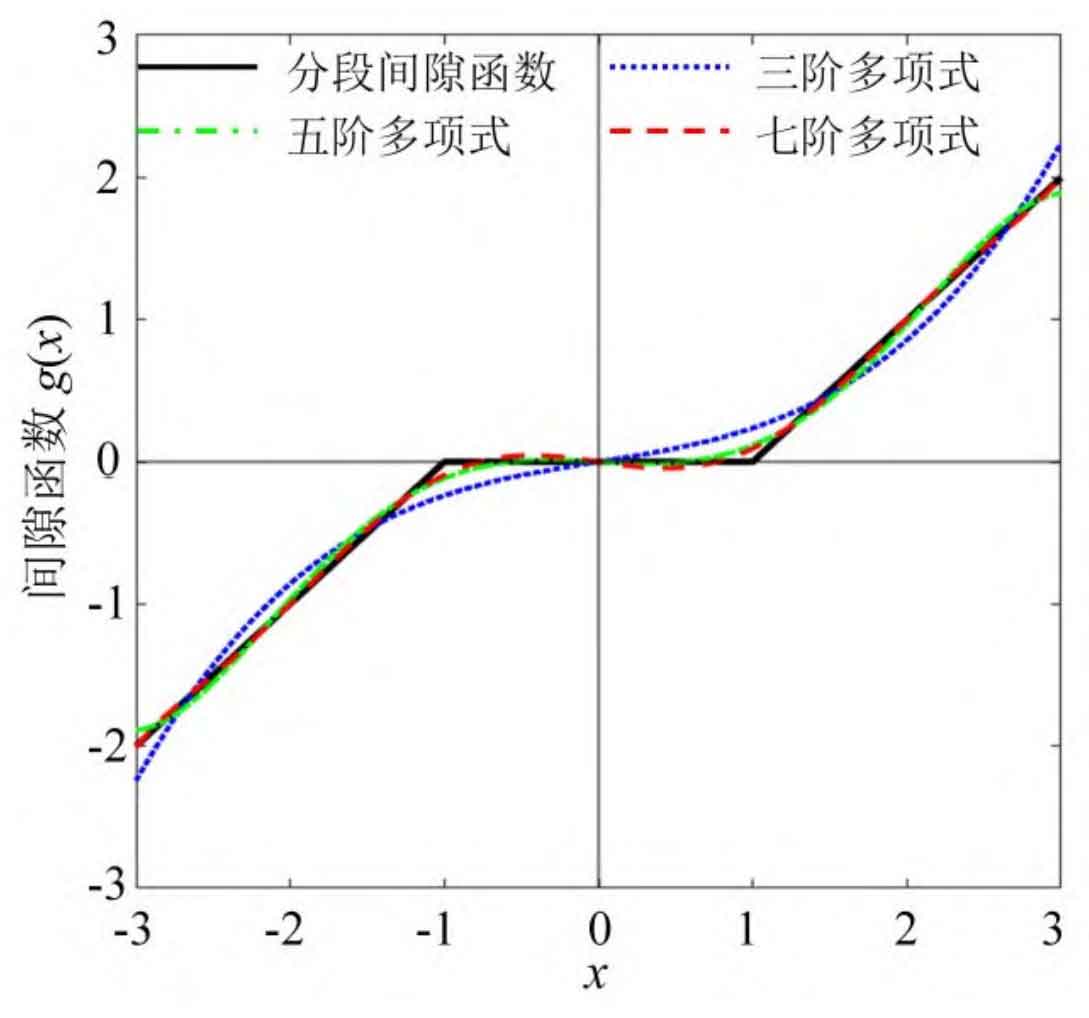
As shown in the figure, the initial piecewise linear function g (x) of helical gear and its polynomial fitting curve of each order are shown. It can be seen that the deviation gradually decreases with the increase of the fitting order.
| Polynomial term | Third order | Fifth order | Seventh order |
| x | 0.173 86 | -0.052 678 | -0.155 49 |
| X^3 | 0.064 75 | 0.180 83 | 0.283 3 |
| x^5 | — | -0.011 69 | -0.036 636 |
| x^7 | — | — | 0.001 711 7 |
In comprehensive consideration of calculation efficiency and accuracy, the 7-order polynomial is used to express the function g (x) of helical gear backlash: