Figure 1 shows the dimensionless vibration displacement u and v with load ratio of p, g tooth pairs and q, g tooth pairs λ Bifurcation diagram of change. For p and g tooth pairs, with the increase of load ratio, the system moves from quasi-periodic( λ= 0 → 0.57) enter a stable single-cycle motion state( λ= 0.57→1)。 Similarly, for the q and g tooth pairs, with the increase of the load ratio, the system successively experiences chaotic motion state and stable single-cycle motion state.
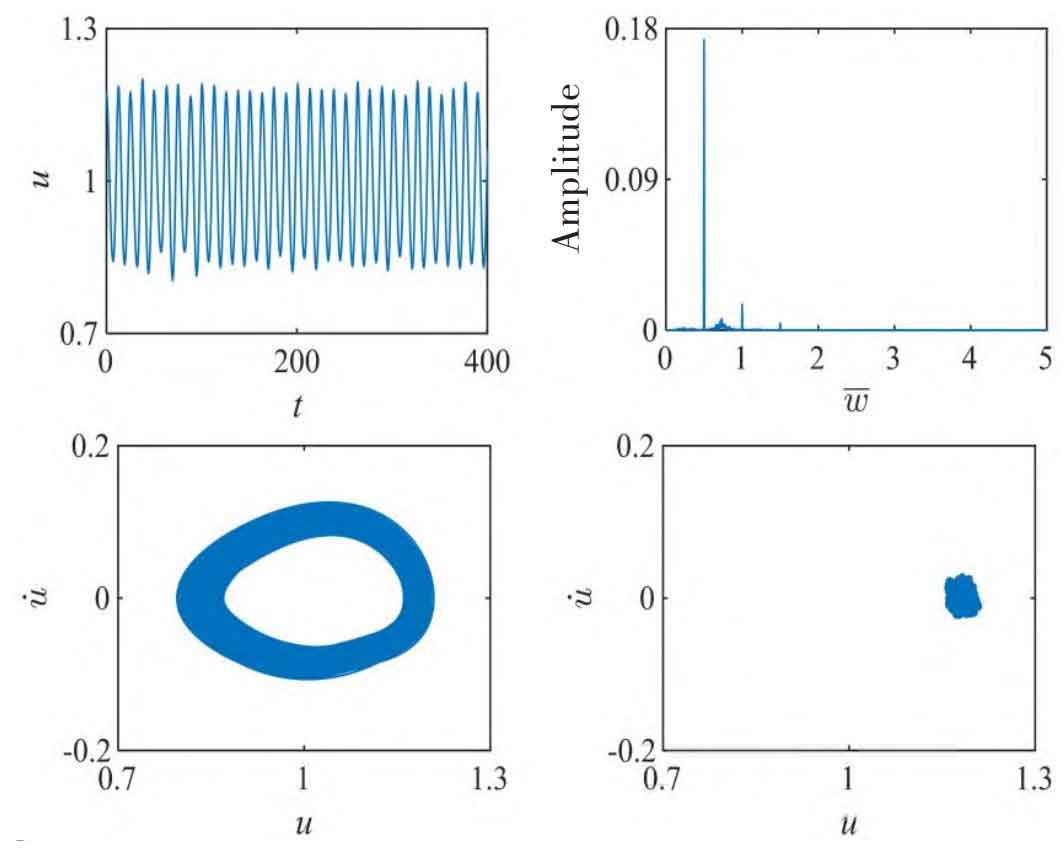
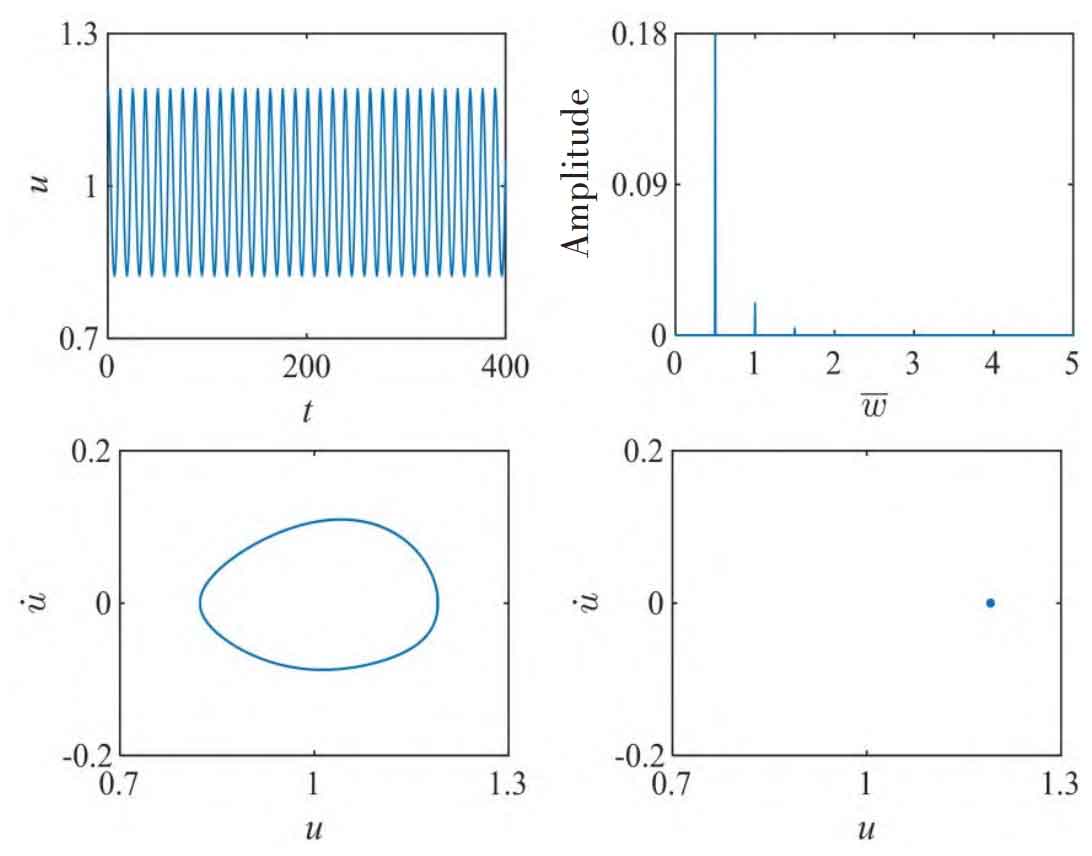
Figure 2-3 shows the system under different load ratios λ Time frequency curve, phase diagram and Poin ⁃ car é cross section of dimensionless vibration displacement u. When λ When the value is 0.1, the parameter u presents quasi-single-period vibration in the interval (0.7, 1.3), indicating that the p and g tooth pairs switch back and forth between the meshing and disengagement states of helical gears. The FFT diagram contains an obvious peak frequency of 0.5 (fundamental frequency) and a small amplitude vibration frequency of 1.0 (double frequency). When λ When it is 0.8, the system is in a stable single-cycle motion state, and the p and g tooth pairs are also switched between the helical gear spur gear meshing and the disengagement state.
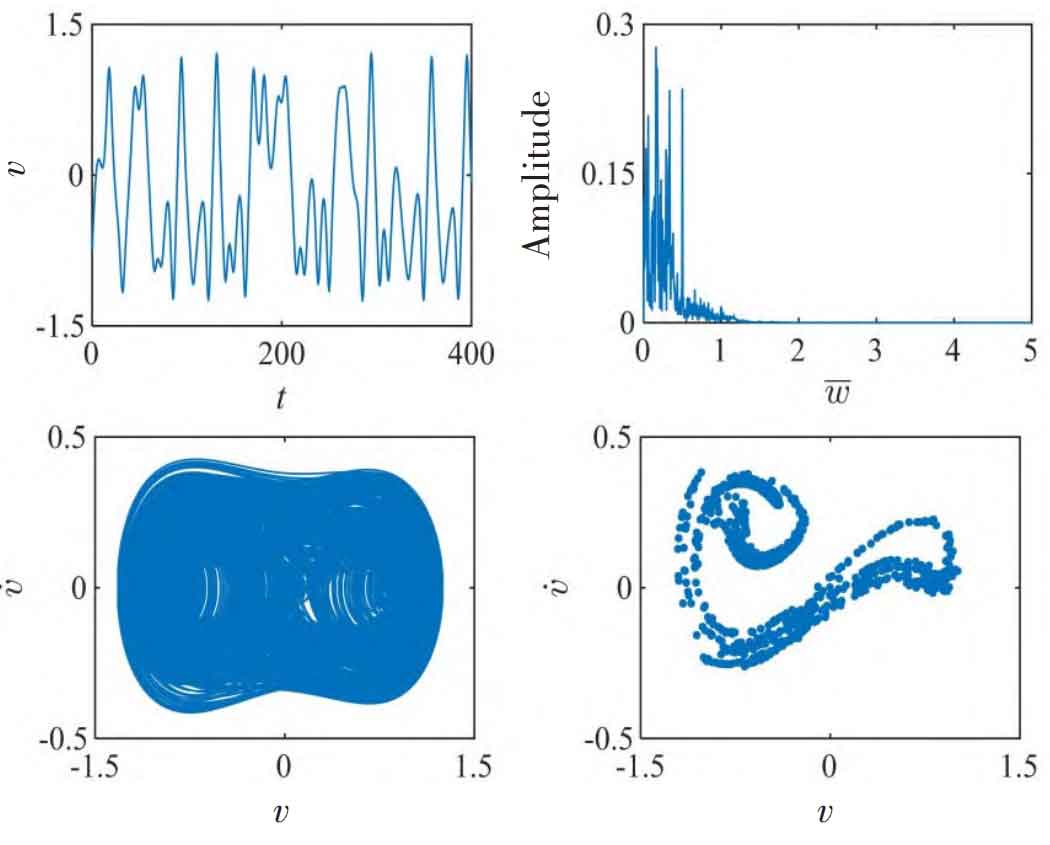
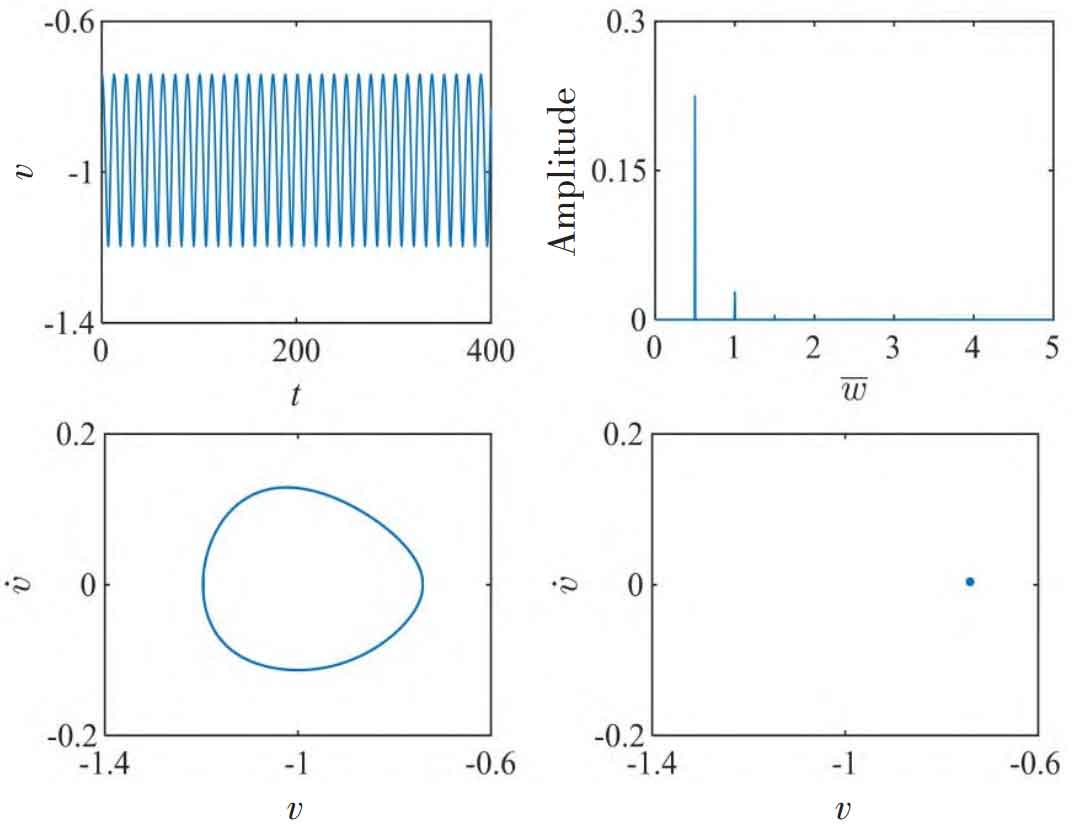
Figure 4-5 shows the system under different load ratios λ The dynamic characteristics of dimensionless vibration displacement v. When λ When the value is 0.1, the parameter v oscillates in the range (- 1.5, 1.5), indicating that there are three motion states of helical gear spur gear meshing, disengagement and back gear meshing in the movement process of q and g gear pairs, and the front impact and back impact of helical gear teeth alternate. The FFT diagram presents a discrete spectrum with a certain width. At the same time, its phase space trajectory and Poincar é section show that the system is in chaotic motion. When λ When it is 0.8, the system enters a stable single-cycle motion state, and the q and g gear pairs switch between the helical gear spur gear meshing and the disengagement state. Its FFT diagram contains an obvious peak frequency of 0.5 (fundamental frequency) and a small amplitude vibration frequency of 1.0 (second harmonic).