Figure 1 shows the dimensionless vibration displacement u and v with load ratio of p, g tooth pairs and q, g tooth pairs λ Bifurcation diagram of change. For p and g tooth pairs, the system successively undergoes quasi-periodic motion with the increase of load ratio( λ= 0 → 0.13) and stable three-cycle motion state( λ= 0.13→1)。
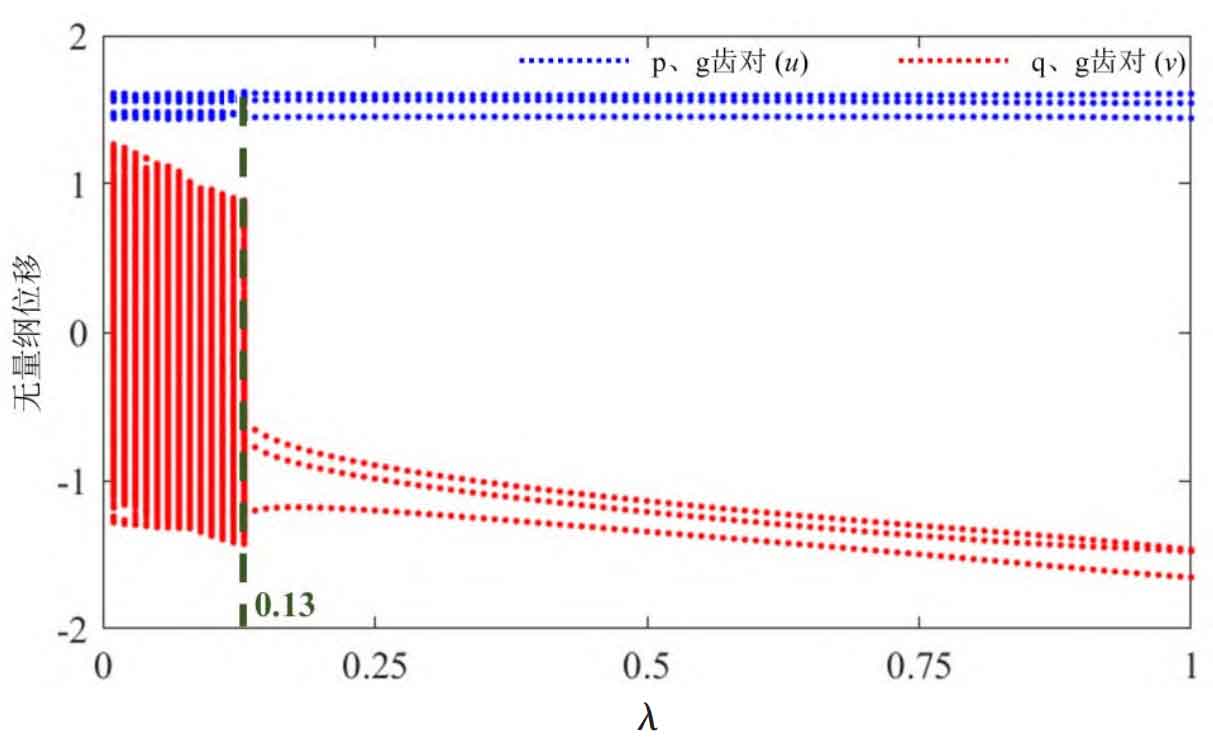
For the q and g tooth pairs, with the increase of the load ratio, the system shows chaotic motion state and three-period motion state. Compared with the light load condition, the nonlinear range (chaotic state and quasi-periodic motion state) of the system under heavy load is relatively narrow, which indicates that when adjusting the parallel input load ratio of the system, the heavy load system is easier to avoid the unstable range and enter the stable periodic motion state.
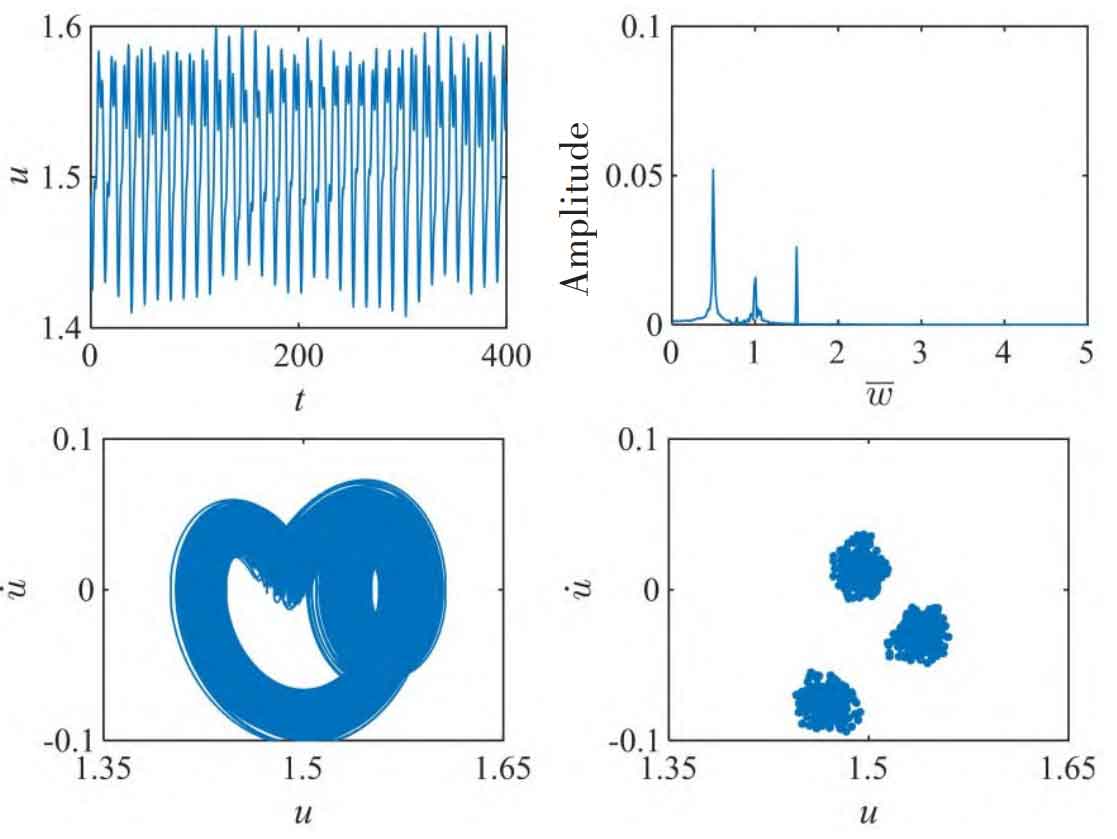
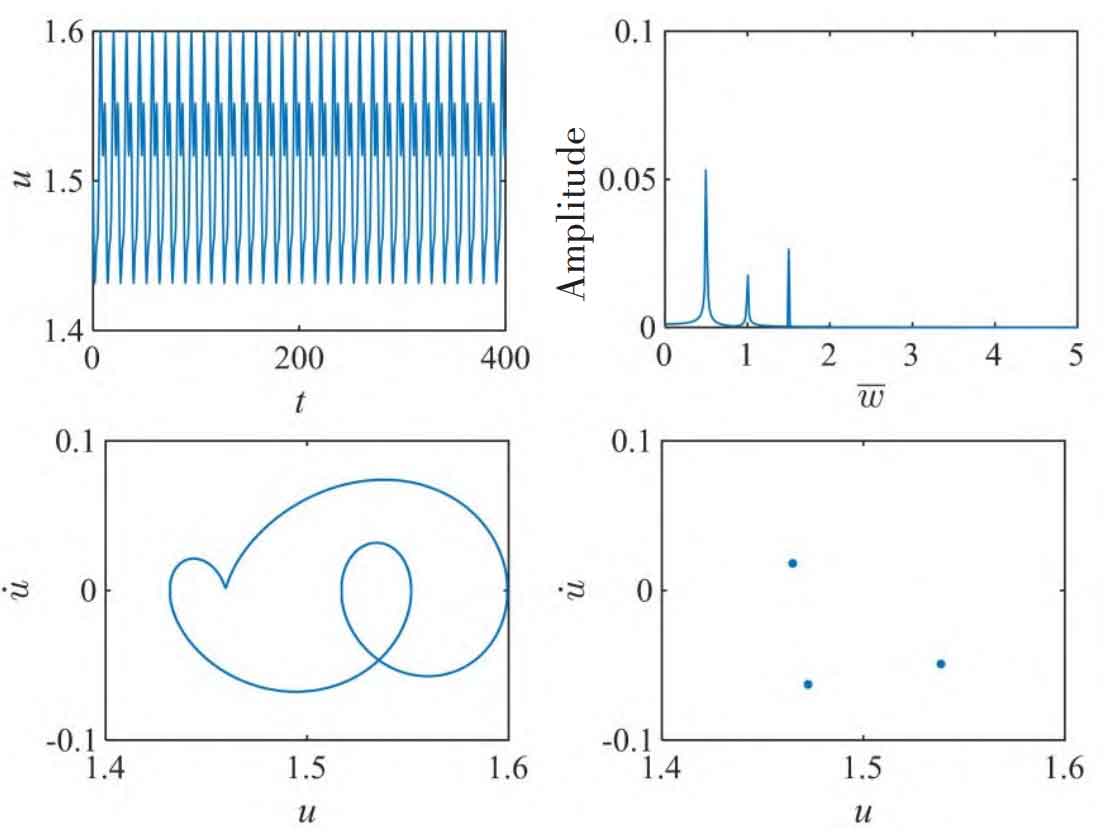
Figure 2-3 shows the system under different load ratios λ The dynamic characteristics of the dimensionless vibration displacement u. When λ When the value is 0.1, the parameter u oscillates in the range (1.4, 1.6), indicating that the p and g tooth pairs are always in the helical gear spur gear meshing state. Its FFT diagram contains obvious peak frequencies of 0.5 (fundamental frequency), 1.0 (second harmonic) and 1.5 (third harmonic). The system phase diagram presents a closed curve of multiple winding. The points on the Poincar é section are mainly concentrated near three points. At this time, the system approximately corresponds to three periodic motions. When λ When it is 0.8, the parameter u presents periodic vibration in the interval (1.4, 1.6). Its phase diagram and Poincar é section show that the system presents stable three-period motion.
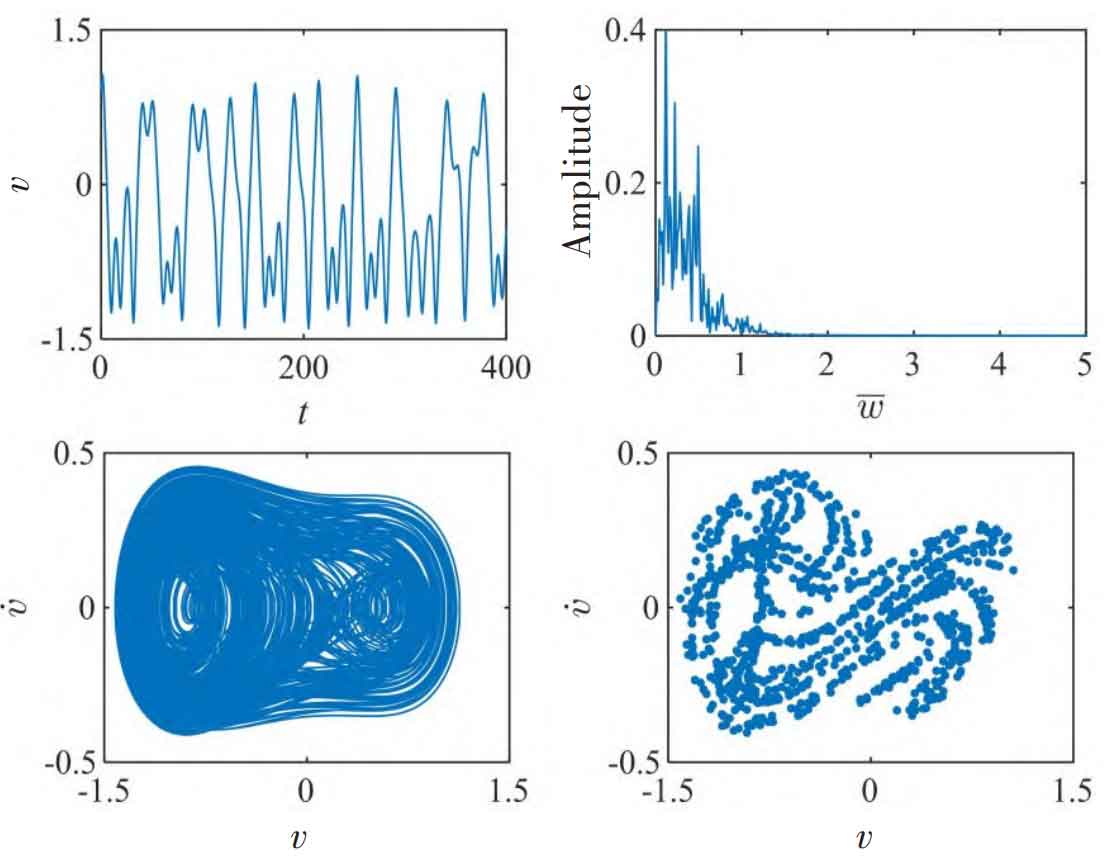
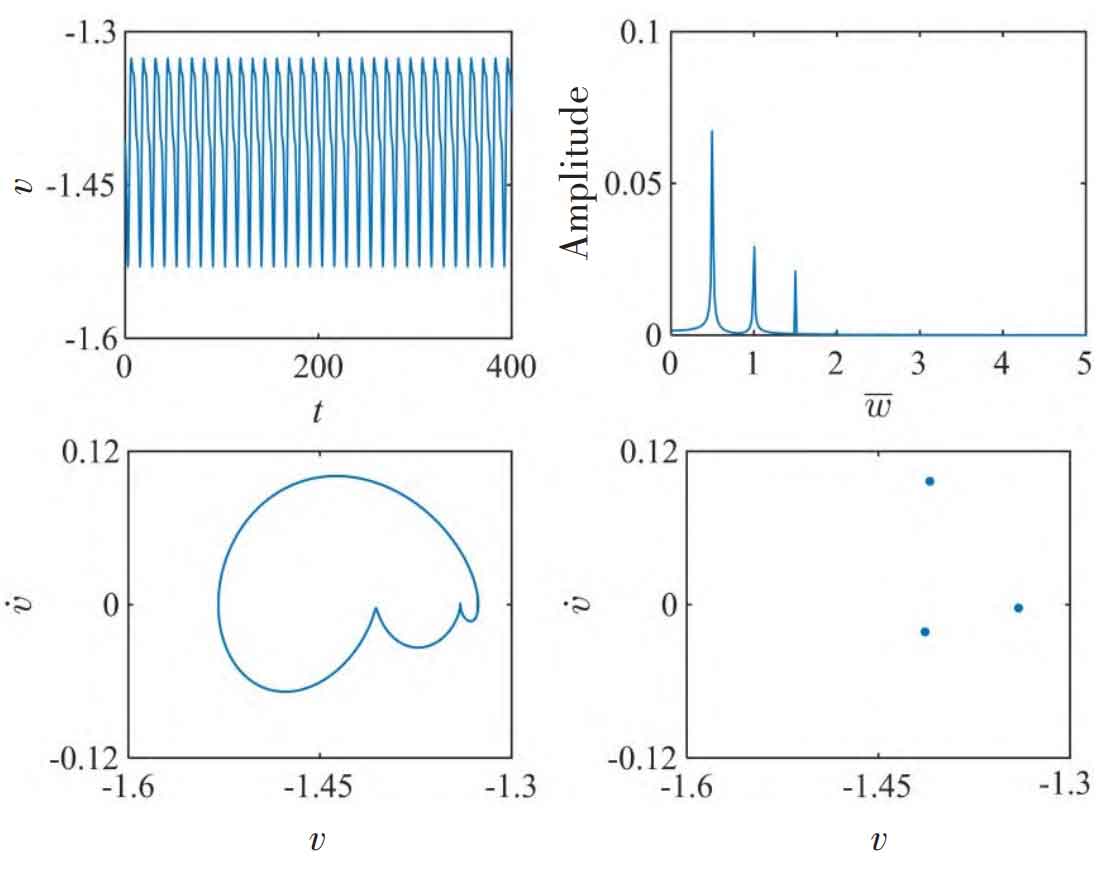
Figure 4-5 shows the system under different load ratios λ The dynamic characteristics of dimensionless vibration displacement v. When λ When it is 0.1, the dynamic behavior of the parameter v is similar to that of the light load condition, which is characterized by oscillation in the interval (- 1.5, 1.5), that is, there are three motion states of helical gear spur gear meshing, disengagement and helical gear back gear meshing during the movement of the q and g gear pairs, and the front impact and back impact of the helical gear teeth alternate. The FFT diagram presents a discrete spectrum with a certain width. At the same time, its phase space trajectory and Poincar é section show that the system is in chaotic motion. When λ When it is 0.8, the parameter v vibrates periodically in the interval (- 1.6, – 1.3), indicating that the pair of q and g teeth is always in the helical gear back tooth meshing state. The frequency domain signal of meshing displacement has peak frequencies of 0.5 (fundamental frequency), 1.0 (second harmonic) and 1.5 (third harmonic) at the same time, and the amplitude decreases gradually. Its phase diagram and Poincar é section show that the system presents a stable three-period motion state.