Generally, the vibration of low-order natural frequency has a great impact on the dynamic performance of the structure, while the modal frequency far away from the vibration source has a small contribution to the actual vibration of the structure. Therefore, the first six natural frequencies and corresponding vibration modes of the system can usually be extracted when conducting contact modal analysis to meet the needs of engineering.
| Order | Natural frequency without prestress/Hz | Natural frequency with prestress/Hz | Deformation/mm | Vibration stress/MPa |
| 1 | 711.47 | 1389.2 | 8.947 | 711.47 |
| 2 | 3115.2 | 4368.3 | 14.396 | 3115.2 |
| 3 | 4373.8 | 4707 | 33.245 | 4373.8 |
| 4 | 4708.9 | 5040.9 | 33.245 | 4708.9 |
| 5 | 5056.1 | 5051.1 | 26.415 | 5056.1 |
| 6 | 5215 | 5496.8 | 28.935 | 5215 |
Based on the static analysis, the contact modal analysis of the spiral bevel gear pair is carried out, and the relevant frequencies and vibration modes (as shown in the table) and the first six vibration modes of the spiral bevel gear pair are obtained as shown in the figure. Compared with the results of free mode analysis, the following conclusions are drawn.
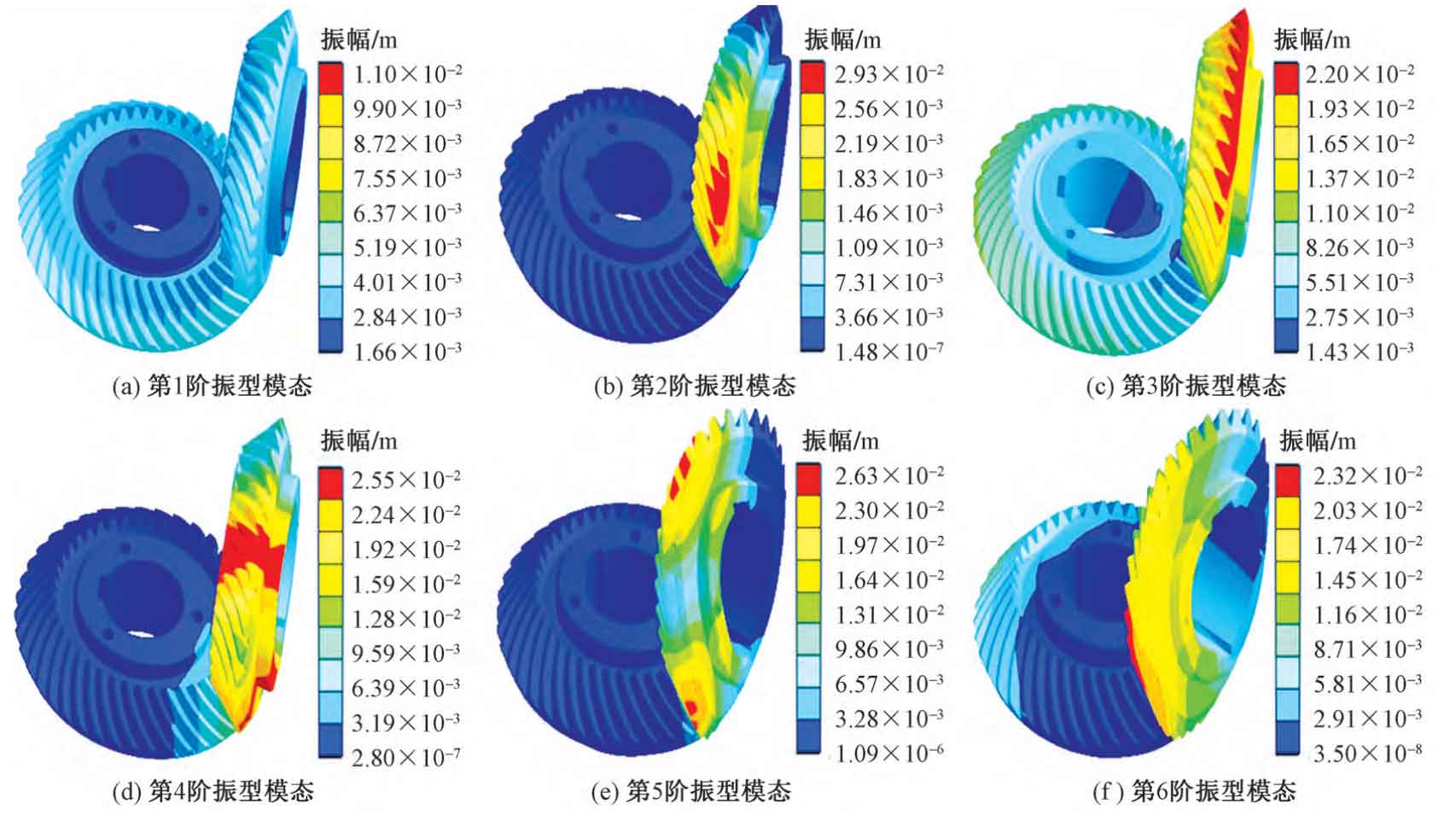
(1) Under the prestress condition, the natural frequency of the spiral bevel gear pair increases slightly, and the vibration modes of each order are similar to those without prestress. In the contact mode state, it has little influence on the dynamic characteristics of spiral bevel gears. The first step is the circumferential vibration and rolling vibration of the driving gear and the passive gear, and the radial vibration and tensile vibration of the passive gear; The second step is the up and down vibration of one end of the passive gear; The third step is that the passive gear vibrates from one side to the other; The fourth step is the passive gear vibration folded in the opposite direction; The fifth step is the torsional and circumferential folded vibration of the passive gear in four directions; The sixth stage is that the drive gear is subject to telescopic vibration at six ends, and the passive gear is subject to vibration and folding in the circumferential direction.
(2) In the free mode, the frequencies of the 7th and 8th order are very close, which is equivalent to the 1st and 2nd order frequencies, so it is easy to cause resonance. In contact mode, the second and third frequencies are very close, and resonance is easy to occur. Therefore, when designing spiral bevel gears, the frequency region caused by external excitation and meshing internal force should be avoided as far as possible.
(3) The natural frequency of the system is related to the structural stiffness matrix and mass matrix. The influence of load on mass matrix can be ignored, and the frequency increases with the increase of structural stiffness.
(4) Through the spiral bevel gear rotation frequency formula fr=n/60 and the meshing vibration frequency formula fh=nZ/60, it can be concluded that the internal excitation of the spiral bevel gear will not cause the spiral bevel gear itself to produce severe vibration.
