Abstract
The dynamic reliability of wind power gear transmission systems is a crucial factor influencing the overall performance and longevity of wind turbines. This study focuses on the reliability assessment of a 2 MW wind turbine gearbox, comprehensively considering internal excitations such as time-varying meshing stiffness and comprehensive errors. A gear-shaft-bearing dynamics model is established to obtain the dynamic meshing forces under constant load conditions. Furthermore, the study incorporates external excitations based on Weibull random wind speed models to analyze the stress-time history of gears under variable loads. By integrating the traditional stress-strength interference model with Gamma stochastic processes and considering part failure correlations, a hybrid Copula model is constructed to evaluate the dynamic reliability of the gearbox system. The results demonstrate that tooth surface contact fatigue is predominant in the early stages of service, whereas tooth root bending fatigue emerges primarily in the middle and late stages. This comprehensive analysis provides valuable insights for the reliability design and maintenance strategies of wind turbine gearboxes.
Keywords: wind turbines, Copula, gear, reliability, strength degradation, transmission system, failure correlation
Introduction
Wind power, as a renewable energy source, has gained significant attention in recent years due to its clean and sustainable nature. However, the reliability of wind turbine gear transmission systems (GTS) is essential to ensure their continuous and efficient operation. The gearbox, as a critical component of wind turbines, is subjected to complex dynamic loads resulting from the variation in wind speed. These loads, coupled with internal excitations, lead to fatigue and wear, eventually affecting the overall reliability of the system.
Several studies have investigated the reliability of wind turbine gearboxes, primarily focusing on individual components or simplified models. However, few studies have comprehensively addressed the dynamic reliability of the entire transmission system, considering both internal and external excitations and part failure correlations. This study aims to fill this gap by developing a detailed dynamics model and a reliability assessment framework that integrates these factors.
Dynamics Modeling of the Gear Transmission System
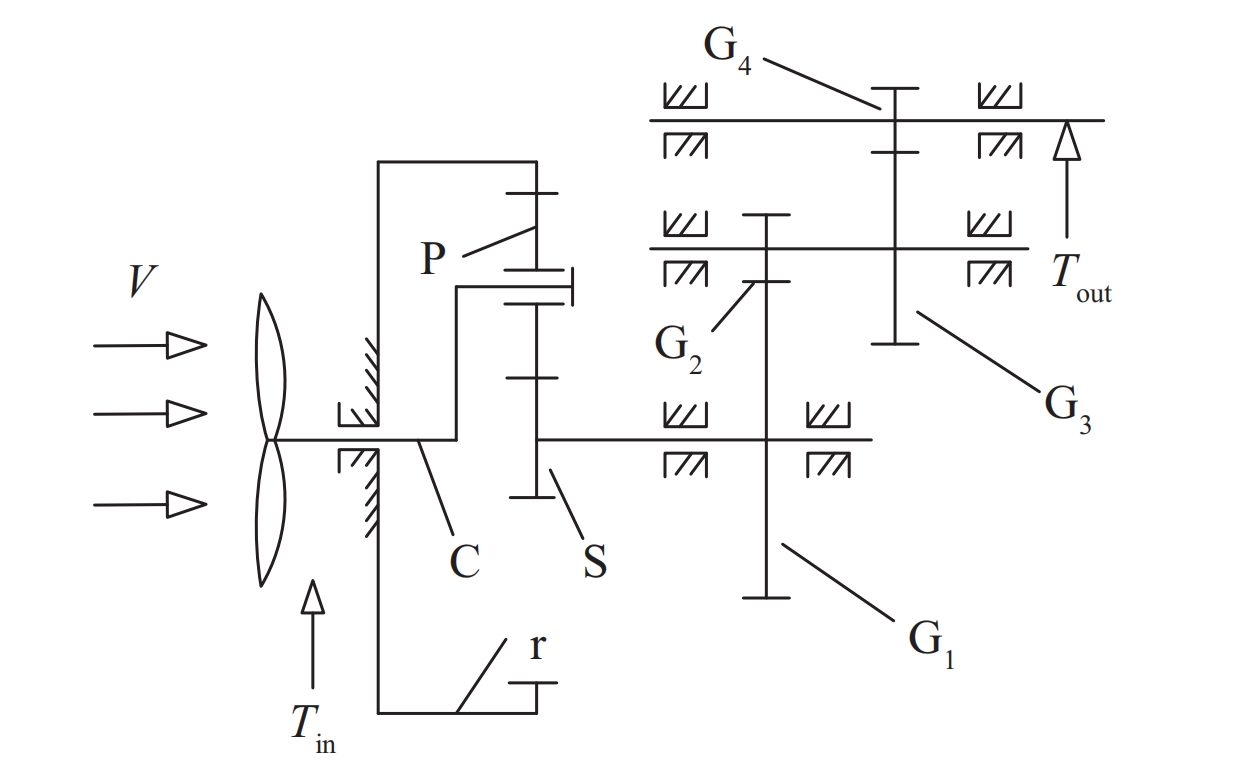
Gearbox Configuration
The wind turbine gearbox considered in this study adopts an NGW (Normal Gear Wheel) planetary transmission coupled with two-stage parallel shaft transmission. The structure of the gearbox.
Model Establishment
To accurately model the dynamic behavior of the gear transmission system, a combination of lumped parameter and finite element methods is employed. The planetary gear train is modeled using the lumped parameter approach, while the parallel shaft system is modeled using finite element analysis.
- Planetary Gear Train Model: The planetary gear train is modeled considering the torsional and translational degrees of freedom for each component. The dynamic equations are derived using Lagrangian mechanics.
- Parallel Shaft Transmission Model: The parallel shaft transmission is modeled using a finite element approach, dividing the system into multiple nodes. The dynamic equations are obtained based on the generalized finite element method.
Dynamic Meshing Forces
Under constant load conditions, the dynamic meshing forces between gear pairs are obtained by solving the dynamic equations. the meshing forces for various gear pairs, exhibiting periodic variations.
Random Wind Load and Stress Analysis
Random Wind Speed Model
The external excitation of the gearbox primarily arises from the variation in wind speed. The Weibull distribution is commonly used to model natural wind speeds, with the probability density function (PDF) and cumulative distribution function (CDF) given by:
fW(v)=(ck)(cv)k−1e−(cv)k
FW(v)=1−e−(cv)k
where k and c are the shape and scale parameters, respectively, and v is the wind speed.
Based on field data from a wind farm in Xinjiang, China, the parameters k and c are estimated to be 4.9 and 8.7, respectively. simulated time series of random wind speeds.
System Input Torque and Stress-Time History
The input torque to the gearbox is calculated using the power coefficient and air density, as described in Section 2.2. The dynamic stress-time history of each gear is then derived using the quasi-static approach, considering both the dynamic meshing forces and variable input torque.
Dynamic Reliability Modeling
Initial Strength and Strength Degradation
The initial strengths of gears for contact fatigue (\sigma_{H0}\)) and bending fatigue (\(\sigma_{F0}\)) are calculated based on standard fatigue limit formulas and material properties. Strength degradation over time is modeled using the Gamma stochastic process, which is characterized by the shape parameter \(v(t) and scale parameter μ. The PDF of the Gamma process is given by:
G(d∣v(t),μ)=Γ(v(t))μv(t)dv(t)−1e−μdfor d≥0
Table 1 and Table 2 summarize the P-S-N curve parameters and degradation parameters for the gear material (20CrMnTi steel) used in this study.
Table 1: P-S-N Curve Parameters of 20CrMnTi Steel
| Survival Rate ((P)) | Curve Parameter m | Curve Parameter C |
|---|---|---|
| 0.99 | 28.57 | 1.08 × 10¹⁰ |
| 0.95 | 21.89 | 7.10 × 10⁷ |
| 0.90 | 20.24 | 3.27 × 10⁷ |
| 0.50 | 14.04 | 1.16 × 10⁵ |
Table 2: Degradation Process Parameters for Each Gear
| Gear | Contact Fatigue | Bending Fatigue |
|---|---|---|
| G1 | v=0.0015, μ=1.0312 | v=0.0015, μ=0.5663 |
| G2 | v=0.0014, μ=0.9065 | v=0.0014, μ=0.5067 |
| … | … | … |
Stress-Strength Interference Model
The stress-strength interference model is employed to assess the reliability of individual gears. The failure probability ((P_f)) is calculated as the probability that the stress exceeds the degraded strength:
Pf=P(σ(t)>σ0−D(t))
where σ(t) is the dynamic stress at time t, σ0 is the initial strength, and D(t) is the strength degradation at time t.
Failure Correlation and Copula Models
Part failures within the gear transmission system often exhibit correlations, both at the component level and the system level. To capture these correlations, a hybrid Copula model is constructed using multiple Copula functions (Gumbel, Clayton, and Frank).
The functional relationships for contact fatigue ((g_1)) and bending fatigue ((g_2)) are defined as:
g1=σH0−DH−σH(t)
g2=σF0−DF−σF(t)
where DH and DF are the degradation amounts for contact and bending fatigue, respectively.
A nested Copula structure is employed to model the failure correlations between gears and subsystems. The joint failure probability of multiple gears is calculated using the appropriate Copula function, which is then integrated into the system-level reliability analysis.
Results and Discussion
Stress-Time History and Distribution
The stress-time histories of selected gears under random wind loads exhibit fluctuating patterns with reduced periodicity compared to constant load conditions. The stress distributions, follow either normal or lognormal distributions, confirmed using the Kolmogorov-Smirnov (K-S) test.
Dynamic Reliability Curves
The dynamic reliability curves for various gears under different failure modes are presented. These curves demonstrate that the reliability decreases gradually over time, with a steeper decline in the middle and late stages of operation.
The results indicate that contact fatigue is the primary failure mode in the early stages, while bending fatigue becomes more prominent in the middle and late stages. The critical components, such as the sun gear and high-speed pinion gears, exhibit lower reliability and require closer monitoring and maintenance.
Failure Correlation and System Reliability
The hybrid Copula model captures the failure correlations at both the component and system levels. The estimated parameters for the nested Copula functions are presented in Table 4. The system reliability curve, considering failure correlations, is compared with the curve assuming independent.
Table 4: Copula Related Parameters for Planetary Gear Train
| Copula Function | C1(⋅) | C2(⋅) | C3(⋅) | C4(⋅) | C5(⋅) | C6(⋅) |
|---|---|---|---|---|---|---|
| εG | 0.000 | 0.004 | 0.000 | 0.104 | 0.993 | 0.989 |
| εC | 0.048 | 0.000 | 0.038 | 0.587 | 0.000 | 0.000 |
| εF | 0.952 | 0.996 | 0.962 | 0.309 | 0.007 | 0.011 |
| θ | – | – | – | 2.193 | 17.42 | 17.5 |
| α | – | – | – | 1.0 | 190.9 | 1.0 |
| γ | – | – | – | 0.0842 | 0.742 | 0.76 |
The system reliability curve considering failure correlations more accurately reflects the actual operating conditions, with a slower decline in reliability compared to the independent failure assumption. This finding highlights the importance of considering failure correlations in reliability assessments.
Conclusion
This study presents a comprehensive framework for assessing the dynamic reliability of wind turbine gear transmission systems, considering both internal and external excitations and part failure correlations. By establishing detailed dynamics models, integrating random wind load simulations, and employing hybrid Copula models, the study provides valuable insights into the reliability behavior of wind turbine gearboxes.
The key findings include:
- Dynamic Meshing Forces and Stress Distributions: Under random wind loads, the dynamic meshing forces and stress distributions exhibit fluctuating patterns with reduced periodicity.
- Failure Modes and Reliability Curves: Contact fatigue is the primary failure mode in the early stages of operation, while bending fatigue becomes more prominent in the middle and late stages. Critical components, such as the sun gear and high-speed pinion gears, require close monitoring.
- Failure Correlations and System Reliability: Considering failure correlations leads to a more accurate assessment of system reliability, with a slower decline compared to assuming independent failures.
This study provides a reference for the reliability design and maintenance strategies of wind turbine gearboxes, emphasizing the importance of comprehensive modeling and failure correlation analysis.
