
1. Introduction
Spur gear play a crucial role in mechanical transmission systems due to their simplicity and high efficiency. However, in certain applications, the standard spur gear design may not meet the requirements for performance and durability. Tooth profile modification, which involves altering the shape of the gear teeth, has emerged as a promising solution to address these limitations. This article focuses on the research of the meshing dynamic characteristics of cylindrical spur gear with tooth profile modification.
1.1 Background and Significance
In mechanical engineering, the performance of gear systems directly impacts the overall efficiency and reliability of machinery. Traditional spur gears may suffer from issues such as vibration, noise, and reduced load-carrying capacity. By modifying the tooth profile, it is possible to optimize the meshing process, improve load distribution, and enhance the dynamic behavior of spur gear system. This research aims to contribute to the understanding and application of tooth profile modification techniques in spur gear design.
1.2 Research Objectives
The main objectives of this study are as follows:
- To establish an analytical model for the transmission of modified spur gear that takes into account various factors affecting the meshing process.
- To investigate the influence of tooth profile modification on the time-varying meshing stiffness (TVMS) and dynamic characteristics of spur gear systems.
- To analyze the effects of different types of tooth profile modification, including single tooth profile modification and compound modification, on spur gear performance.
1.3 Research Methodology
The research methodology employed in this study involves the following steps:
- Literature Review: A comprehensive review of existing research on spur gear meshing stiffness, dynamic characteristics, and tooth profile modification was conducted to identify the research gaps and build a theoretical foundation.
- Model Development: An analytical model for the transmission of modified spur gear was established, considering factors such as Hertz contact stiffness, bending stiffness, shear stiffness, axial compression stiffness, and fillet foundation stiffness.
- Numerical Simulation: Using the developed model, numerical simulations were carried out to study the effects of tooth profile modification on TVMS and dynamic characteristics. Parameters such as spur gear geometry, material properties, and operating conditions were varied to analyze their influence.
- Case Studies: Specific case studies were conducted to validate the model and analyze the practical implications of tooth profile modification. The results were compared with those of standard spur gear to evaluate the performance improvement.
2. Time-Varying Meshing Stiffness Analysis Model
The accurate prediction of the dynamic performance of spur gear transmissions requires a reliable model for the time-varying meshing stiffness (TVMS). In this section, a detailed analysis model for TVMS is presented, which forms the basis for understanding the meshing behavior of modified spur gear.
2.1 Stiffness Calculation Based on Potential Energy Method
The potential energy method is utilized to calculate the stiffness of spur gear teeth. The total potential energy of spur gear tooth is composed of several components, including Hertzian contact energy, bending energy, shear energy, axial compression energy, and fillet foundation energy. These energy components can be expressed mathematically as follows:
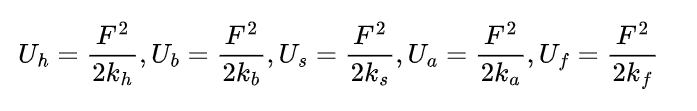
where F is the resultant force acting on the meshing gear teeth, and Kh,Kb,Ks,Ka,Kf are the stiffness coefficients corresponding to the different energy components.
The total potential energy of a single gear can be described in terms of these component stiffnesses as:
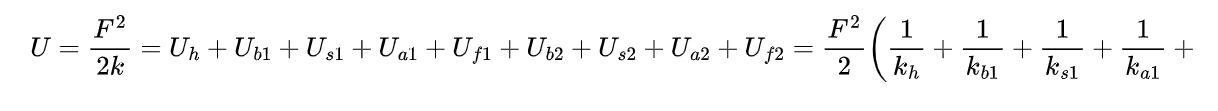
where K is the total meshing stiffness during engagement, and the subscripts 1 and 2 denote the driving gear and the driven gear, respectively.
The TVMS of the meshing gear pair can then be expressed as:
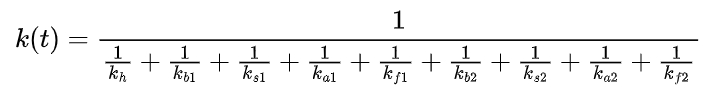
where t represents time, and the stiffness values vary with the meshing position of spur gear.
2.2 Geometric Relationship Analysis
For spur gear with equal modification coefficients, the pitch circle and the base circle remain unchanged, and their geometric relationships are similar to those of equivalent standard spur gear. However, for spur gear with unequal modification coefficients, the geometric relationships need to be re-evaluated due to the uncoordinated changes in these circles.
In particular, during gear meshing, the pitch circle of spur gear no longer coincides with the reference circle, resulting in a change in the position of pure rolling compared to standard spur gear. Based on the fundamental theory of modified spur gear, the geometric relationship at the start of gear meshing.
When spur gear and pinion start to mesh, contact occurs at point A between the line of action and the addendum circle of spur gear. As spur gear rotates, the gear and pinion eventually separate at the intersection of the line of action and the addendum circle of the pinion. The angles of the pinion and gear can be expressed as:
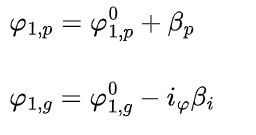
where ig is the transmission ratio, the superscript 0 denotes the initial value of the angle, p and g the subscripts and represent the pinion and gear, respectively.
The angles φ2 of the pinion and gear can be calculated as:
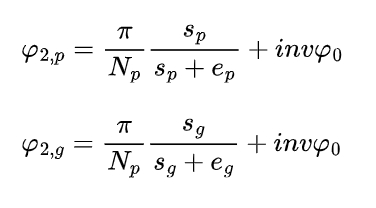
where Np and Ng are the numbers of teeth of the pinion and gear, respectively; Sp and Sg are the tooth thicknesses of the pinion and gear; ep and eg are the differences between the pitch and tooth thicknesses of the pinion and gear; φ0 is the reference pressure angle; and is the involute function.
The initial values of the angles can be obtained from the following equations:
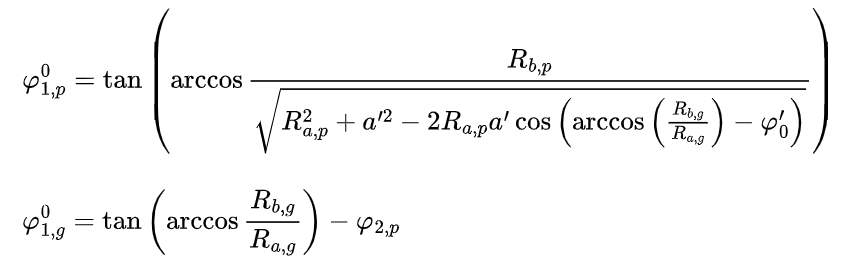
where Rb,p and Rb,g are the base circle radii of the pinion and gear, respectively; Rα,p and Rα,g are the addendum circle radii of the pinion and gear, respectively; and α’ is the modified center distance.
3. Research Framework for Modified Spur Gear
Based on the established TVMS model, a research framework for analyzing the performance of modified spur gear is proposed in this section. This framework integrates various aspects of spur gear dynamics to comprehensively evaluate the effects of tooth profile modification.
3.1 Gear System Dynamics Model
A six-degree-of-freedom dynamics model for spur gear and pinion system is developed. Considering that the meshing stiffness mainly affects the in-plane vibration of spur gear pair rather than the axial vibration, only the motions along and perpendicular to the line of action and the rotations are considered. The shaft ends are connected to bearings, and a parallel spring-damper device is used to model the bearing support. The dynamic equations of the system can be written as follows:
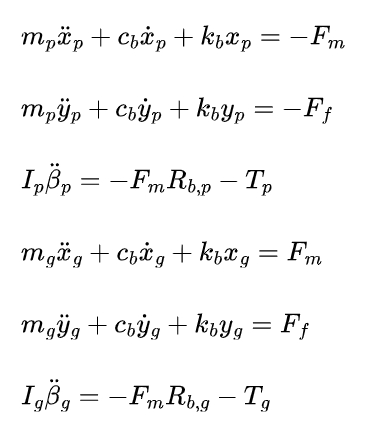
where mp and mg are the masses of the pinion and gear, respectively; Ip and Ig are the moments of inertia of the pinion and gear, respectively; cb and kb are the damping and stiffness coefficients of the bearings, respectively; Tp and Tg are the driving torque and load torque, respectively; Fm and Ff are the meshing force and friction force, respectively, and can be expressed as:
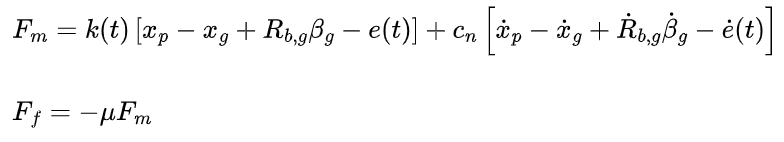
where e(t) is the static transmission error, and μ is the friction coefficient.
The meshing damping coefficient is calculated using the equivalent mass, damping ratio, and average meshing stiffness, and can be expressed as:
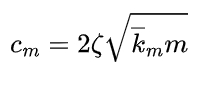
where ξ is the damping ratio, km is the average meshing stiffness, and is the equivalent mass, which can be calculated as m=mpmg/(mp+mg).
3.2 Analysis of Dynamic Characteristics
To analyze the dynamic characteristics of spur gear system, the dynamic transmission error (DTE) is defined as:
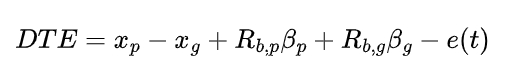
The DTE reflects the deviation between the actual motion of spur gear and the ideal motion, and is an important indicator of the dynamic performance of the spur gear system.
In addition to the DTE, four time-domain indicators are selected to describe the vibration acceleration of spur gear system, namely the root mean square (RMS), the square root of the amplitude (SRA), the peak-to-peak value (PPV), and the kurtosis value (KV). These indicators can be calculated as follows:
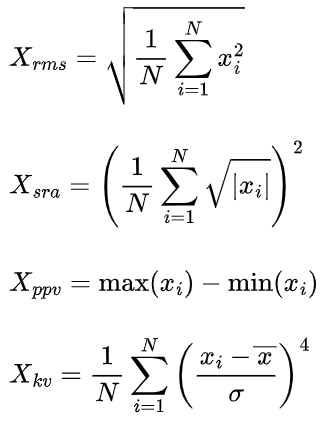
where N is the number of data points, xi is the acceleration value at the i-th time step, x- is the mean value of the acceleration, and σ is the standard deviation.
4. Case Studies
In this section, case studies are conducted to investigate the effects of single tooth profile modification and compound modification on the TVMS and dynamic characteristics of cylindrical spur gear. The results are analyzed and compared to provide practical insights into the design and optimization of modified spur gear.
4.1 Single Tooth Profile Modification
4.1.1 Positive Modification
The influence of positive modification on the tooth stiffness and TVMS of a single gear is first analyzed. The pinion is chosen as the research object, and six modification coefficients ranging from 0 to 0.5 are considered. The tooth stiffness of the pinion under different modification coefficients.
It can be observed that the positive modification coefficient increases the resistance of the tooth to deformation caused by high stiffness. However, the effect of the modification coefficient on the stiffness is different at the beginning and end of meshing. To better describe this effect, a proportional index relative to the standard spur gear is proposed:
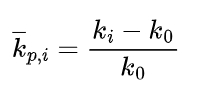
where ki is the stiffness of the pinion with the i-th tooth profile modification, and k0 is the standard stiffness of the unmodified pinion (Pp=0).
The stiffness ratio of the single tooth profile. It can be seen that as the positive modification coefficient increases, the stiffness curve becomes steeper during meshing. The stiffness is higher at the beginning of meshing and lower at the end of meshing.
The TVMS results based on the positive modification coefficient. To clearly illustrate the influence of spur gear meshing stiffness and contact ratio on the modification coefficient, the pinion rotation angle range from 0 to 25 degrees is selected. Overall, the TVMS decreases with an increase in the modification coefficient. Moreover, the rate of change of the TVMS also gradually increases, indicating that positive modification is a sensitive design parameter that requires careful consideration in parameter selection.
The mean and standard deviation of the TVMS for positive modification. The mean and standard deviation describe the average level and oscillation degree of the TVMS, respectively. The changes in these two indicators show a nonlinear relationship with the modification coefficient. The mean value decreases slowly with a slight positive modification and accelerates with a large positive modification. At the same time, the standard deviation increases sharply with a slight positive modification and slows down with a larger positive modification.
To quantitatively analyze the influence of positive modification, the statistical indicators of the DTE for different damping ratios and modification coefficients are extracted and compared with those of the standard spur gear. It can be seen that with an increase in the modification coefficient, all indicators except the PPV at a damping ratio of 0.07 show a monotonically increasing trend. This indicates that positive modification aggravates the vibration of spur gear pair, and the KV is negative within a small range of modification coefficients. The results suggest that a slight modification coefficient reduces the peak value, while a larger modification coefficient increases the peak value. It is also found that the meshing damping coefficient is not sensitive to the statistical indicators.
4.1.2 Negative Modification
In practical engineering applications, negative modification is frequently employed to equalize the fatigue life of the gear and pinion combination. In this particular research, six modification coefficients within the range of 0 to -0.5 are taken into account. The tooth stiffness of the gear corresponding to different modification coefficients.
The negative modification coefficient renders spur gear more pliable in comparison to the standard spur gear. Analogous to positive modification, the modification coefficient exerts varying effects on the stiffness during the commencement and conclusion of meshing. At the onset of meshing, the reduction in stiffness is minimal, and it progressively augments as meshing advances. The rate of alteration of the single gear tooth stiffness for diverse modification coefficients. In contrast to positive modification, the curves denoting the meshing stiffness variation are encompassed within their respective parabolic curves and do not intersect. It is evident that the maximal stiffness loss transpires in the middle of meshing. As the modification coefficient diminishes (in absolute value), the rate of change becomes more pronouncedly curved.
The TVMS outcomes predicated on the negative modification design are depicted. For the sake of lucidity, the pinion rotation angle within the range of 0 to 25 degrees is once again selected. The TVMS of the negatively modified spur gear is inferior to that of the standard gear during the initial stage of meshing. As meshing proceeds, the comprehensive meshing stiffness gradually escalates. Ultimately, the TVMS with a smaller negative modification coefficient will surpass that with a larger negative modification coefficient. Moreover, it can be discerned that the TVMS with a smaller negative modification coefficient exhibits a higher contact ratio, thereby implying that negative modification can enhance the smoothness and continuity of transmission.
The mean and standard deviation of the TVMS for negative modification are presented. The alterations in these two indicators exhibit an approximately linear relationship with the modification coefficient. As the modification coefficient decreases (in absolute value), the mean value progressively ascends, while the standard deviation systematically declines.
To quantitatively assess the impact of negative modification, the statistical indicators of the DTE for diverse damping ratios and modification coefficients are extracted and contrasted with those of the standard spur gear. The results signify that as the modification coefficient diminishes, all indicators manifest a monotonic variation. The RMS and RSA exhibit a downward trend, indicating that negative modification can suppress the vibration of the gear pair. Additionally, the KV ameliorates gradually, albeit the PPV alteration is not conspicuously discernible.
4.2 Compound Modification
In practical scenarios, tooth profile modification is commonly employed to engineer the mechanical properties of the gear and pinion combination. The gear transmission and S gear transmission constitute two forms of compound modification for spur gears. The former possesses a total modification coefficient of 0, while the latter has a non-zero total modification coefficient.
The TVMS curves for different compound modification designs are depicted. The first and second groups pertain to the S gear with a positive total modification coefficient, the third and fourth groups correspond to the S gear with a negative total modification coefficient, the fifth group represents the gear, and the sixth group denotes the standard spur gear. In the first group, and , designated as Group 1; in the second group, and , named Group 2; in the third group, and , labeled Group 3; in the fourth group, and , termed Group 4; in the fifth group, and , called Group 5; and in the sixth group, and , identified as Group 6.
The negative total modification coefficient augments the contact ratio and meshing stiffness, whereas a positive total modification coefficient notably diminishes the contact ratio and meshing stiffness. It is also evident that the gear has a relatively minor influence on the TVMS.
The mean and standard deviation of the TVMS for compound modification are presented. When the total modification coefficient is negative, the mean value of the TVMS is relatively elevated, while the standard deviation exhibits an opposite trend. The influence of different total modification coefficients on the mean value is more dispersed at the pinion modification coefficient and more proximate at the gear modification coefficient.
The variation of the DTE statistical indicators for compound modification under different damping ratios. Similar to the frequency spectrum, the indicators for positive compound modification are higher than those for negative compound modification, with the RSA difference even reaching approximately 15%. The KV curve assumes a zigzag shape, suggesting that the S gear transmission renders the time-domain waveform of the gear system steeper. The statistical indicators of the gear deviate from those of the standard spur gear to a certain extent, primarily due to the equal yet opposite modification coefficients, resulting in disparate modifications for the pinion and gear.
5. Conclusion
In this study, an analytical model for the transmission of modified spur gears was developed, and the influence of tooth profile modification on the operating performance of the gear system was explored. The model enables the direct derivation of the function of the dynamic characteristics of the spur gear system with the pinion rotation angle as the independent variable, considering two distinct geometric designs of tooth profile modification.
Based on the established analytical model and the adopted evaluation method, the impact of tooth profile modification on the TVMS and dynamic characteristics was investigated through numerical simulation. The results indicate that positive modification of a single tooth profile reduces the tooth stiffness and TVMS, while negative modification can enhance the tooth stiffness and TVMS. In the case of compound modification, the S gear transmission with positive compound modification decreases the TVMS but exacerbates the vibration of the gear system. Conversely, the S gear transmission with negative compound modification leads to an increase in the TVMS and a significant reduction in vibration. The gear modification has a relatively minor effect on the time-varying meshing stiffness but a substantial impact on the dynamic characteristics.
This research provides valuable insights and theoretical support for the design and optimization of spur gears with tooth profile modification, contributing to the improvement of gear system performance in mechanical engineering applications. Future research could focus on further refining the model, considering additional factors such as manufacturing tolerances and lubrication conditions, and exploring more advanced modification strategies to meet the evolving demands of high-performance gear transmissions.
