In this study, I investigate the self-locking failure of a typical worm gear mechanism under random vibration environments. Worm gear drives are widely used in actuators and execution units due to their reverse self-locking characteristics, which isolate the load end from reverse interference from the power input end. However, during random vibration tests, I observed that the self-locking capability of the worm gear mechanism can be compromised, leading to unintended movements such as free opening of valves. Through detailed analysis, I identified the primary cause as the self-locking failure of the worm gear pair under vibration. I then propose technical improvements and innovative structural solutions to enhance the self-locking performance of worm gear mechanisms in such conditions. This research involves theoretical derivations, simulation analyses, and experimental validations to ensure the reliability of the proposed design. The findings have significant implications for the design of self-locking actuators composed of worm gear systems in aerospace and other high-vibration applications.
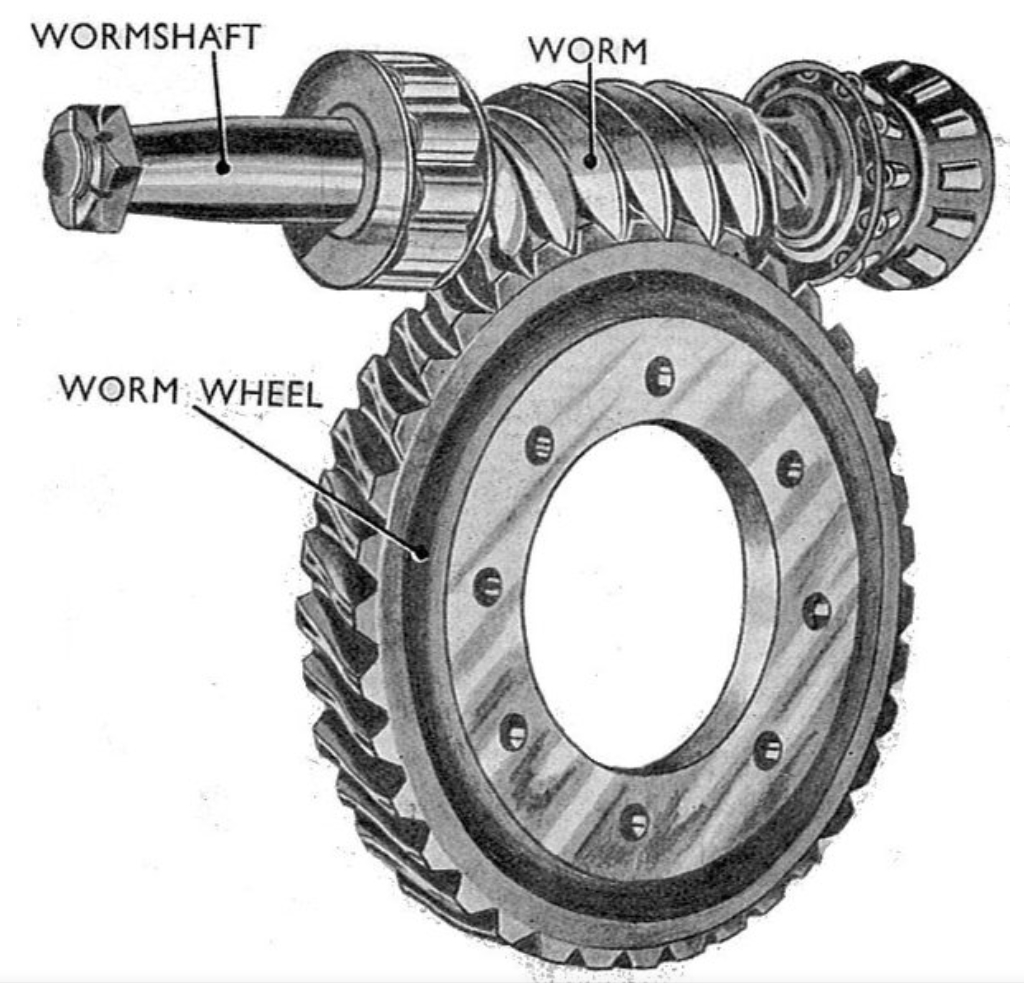
The worm gear mechanism I studied consists of a valve, a linear motion unit, a rotary motion unit, and a motor. The valve component is subjected to external loads, and the motor drives the valve to open and close by overcoming these loads. In the power-off state, the worm gear mechanism should exhibit reverse self-locking, meaning that when a load is applied to the valve end, the valve remains locked in position without movement. The working principle involves the motor directly driving the worm, which rotates the worm gear. This rotational motion is converted into linear motion via a screw pair, pushing the valve to rotate and achieve opening and closing actions. The reverse self-locking function of the worm gear prevents external loads from transmitting reverse torque to the mechanism, ensuring reliability in power-off scenarios. The transmission principle and structure are illustrated in the figure above, highlighting the integration of the worm gear with other components.
To understand the self-locking mechanism of the worm gear, I analyze the forces at the meshing point. The worm experiences tangential force \( F_{t1} \), radial force \( F_{r1} \), and axial force \( F_{a1} \). The interaction between the worm and the worm gear can be simplified as a slider on an inclined plane, where self-locking occurs if the inclination angle \( \alpha \) is less than or equal to the friction angle \( \beta \). For the worm gear, this translates to the lead angle \( \gamma \) of the worm being less than or equal to the friction angle \( \beta \) of the worm gear pair. The lead angle is given by \( \gamma = \arctan\left(\frac{Z_1}{q}\right) \), where \( Z_1 \) is the number of starts on the worm and \( q \) is the diameter quotient. For a single-start worm, standard values of \( q \) and corresponding lead angles are summarized in Table 1.
| Diameter Quotient \( q \) | Lead Angle \( \gamma \) |
|---|---|
| 7.5 | 7°36′ |
| 8 | 7°08′ |
| 9 | 6°20′ |
| 10 | 5°43′ |
| 12 | 4°46′ |
| 16 | 3°35′ |
The friction angle \( \beta \) depends on the friction coefficient \( f \), where \( \beta = \arctan(f) \). The friction coefficient varies with material pairing, as shown in Table 2. For instance, a steel worm paired with a bronze worm gear typically has a friction coefficient ranging from 0.10 to 0.18. Under static conditions, self-locking is achieved if \( \gamma \leq \beta \). However, in vibration environments, the relative motion between the worm and worm gear reduces the effective friction coefficient due to dynamic effects. The relative sliding velocity \( V_s \) is given by \( V_s = \frac{V_1}{\cos \alpha} \), where \( V_1 \) is the circumferential velocity of the worm. As \( V_s \) increases, the friction coefficient decreases, as detailed in Table 3. This reduction can cause the effective friction angle to fall below the lead angle, leading to self-locking failure.
| Worm Material | Worm Gear Material | Friction Coefficient \( f \) |
|---|---|---|
| Steel | Steel | 0.10–0.15 |
| Steel | Cast Iron | 0.10–0.30 |
| Steel | Brass | 0.03–0.15 |
| Steel | Bronze | 0.10–0.18 |
| Relative Sliding Velocity \( V_s \) (m/s) | Friction Coefficient \( f \) |
|---|---|
| 0.010 | 0.110 |
| 0.100 | 0.080 |
| 1.000 | 0.045 |
| 5.000 | 0.022 |
| 10.000 | 0.016 |
| 15.000 | 0.014 |
| 24.000 | 0.013 |
In vibration conditions, the worm gear mechanism is subjected to random accelerations that induce relative motion between the worm and worm gear. This motion arises from imbalances in the motor rotor and the attached worm. The rotor imbalance, due to asymmetrical structure or material inhomogeneity, generates a rotational torque under vibration. Even after balancing, residual imbalances persist, and the addition of the worm exacerbates this issue. The combined system of the motor rotor and worm can experience a net torque that overcomes the friction torque, causing rotation and self-locking failure. I measured the free rotation torque of the worm under vibration to be approximately 1.65 mN·m. To counteract this, I designed a magnetic stabilization mechanism based on the principle of magnetic transmission wheels, which uses permanent magnets to generate a reverse torque that inhibits unwanted rotation.
The magnetic stabilization mechanism comprises a magnetic drive wheel rigidly connected to the worm, a worm end cover, and permanent magnets arranged in a circular pattern. The magnets are radially magnetized and fixed to the end cover, creating a stationary magnetic field. As the magnetic drive wheel rotates, it experiences a circumferential magnetic force that produces a reverse torque. This non-contact approach ensures reliability without introducing additional wear. The structural design was modeled and analyzed to verify its effectiveness. The key parameters include the magnetic force and torque as functions of the rotation angle. For instance, the axial magnetic force \( F_z \) and the torque \( M_z \) around the Z-axis (aligned with the worm axis) were simulated for various angles, as summarized in Table 4. The maximum reverse torque was found to be 4.54 mN·m, which exceeds the vibration-induced torque of 1.65 mN·m, confirming the mechanism’s ability to maintain self-locking.
| Rotation Angle (°) | Axial Magnetic Force \( F_z \) (N) | Torque \( M_z \) (mN·m) |
|---|---|---|
| 0 | 1.28 | -0.04 |
| 15 | 0.89 | -3.27 |
| 30 | 0.00 | -4.54 |
| 45 | -0.89 | -3.18 |
| 60 | -1.27 | 0.06 |
The simulation involved modeling the magnetic components, including permanent magnets made of samarium-cobalt alloy with a remanence \( B_r = 1.18 \, \text{T} \) and coercivity \( H_c = -880 \, \text{kA/m} \). The magnetic forces and torques were calculated using finite element analysis, considering the interaction between the rotating and stationary parts. The results show that the axial magnetic force follows a cosine-like trend with rotation angle, while the torque exhibits a sinusoidal pattern. The total torque \( M_z \) can be expressed as a function of angle \( \theta \): $$ M_z(\theta) = -M_{\text{max}} \sin(2\theta) $$ where \( M_{\text{max}} = 4.54 \, \text{mN·m} \). This torque effectively counteracts the vibration-induced rotation, ensuring that the worm gear remains self-locked.
To assess the impact on motor performance, I analyzed the additional power consumption due to the magnetic stabilization mechanism. The motor has a rated speed of 5600 rpm and a rated torque of 51 mN·m at 3 A current. Assuming a linear torque-current relationship, the current increment per unit torque is approximately 0.058 A/mN·m. Thus, the maximum reverse torque of 4.54 mN·m adds about 0.26 A to the current, resulting in a total of 3.26 A during operation. This is within the allowable limit of 5 A, indicating negligible impact on overall power consumption. Experimental validation was conducted through random vibration tests on the improved worm gear mechanism. The tests involved applying vibration along the Y-axis for 4 hours, after which the valve remained securely locked without free opening. The current measurement confirmed an increase of 0.22 A, consistent with simulations, and the mechanism performed reliably without compromising functionality.
The magnetic stabilization mechanism offers several advantages for worm gear systems. It is compact, requires low magnetic strength, and can be applied to various high-precision indicating mechanisms. The non-contact nature eliminates wear and enhances longevity. By using alternating magnetic poles, the design ensures that the reverse torque always opposes the direction of rotation, providing stable self-locking under vibration. This innovation addresses a critical issue in worm gear applications, particularly in aerospace where reliability under harsh conditions is paramount. Future work could explore optimization of magnet arrangements or materials to further improve performance.
In conclusion, I have demonstrated that the self-locking failure of worm gear mechanisms under vibration can be effectively mitigated through a magnetic stabilization approach. The design generates sufficient reverse torque to prevent unintended rotation, as verified by simulations and experiments. This improvement enhances the reliability of worm gear-based actuators in dynamic environments, with broad applications in engineering systems requiring robust self-locking capabilities. The key takeaway is that incorporating magnetic elements into worm gear designs can significantly improve performance without substantial increases in power consumption or complexity.
