In the field of robotics, end-effectors play a crucial role in enabling direct interaction with the environment. Traditional fully actuated manipulators often involve complex transmission systems and control mechanisms, which can be inefficient for mobile applications. Underactuated manipulators, with fewer actuators and sensors, offer advantages such as lower power consumption, simplified control, and enhanced adaptability. However, existing underactuated designs, such as tendon-driven or linkage-based systems, often exhibit strong dynamic coupling and limited grasping modes. To address these limitations, we propose a novel underactuated manipulator that leverages a planetary gear mechanism to enable both gripping and pulling functions, along with adjustable clamping force without the need for force sensors or complex feedback control. This design utilizes planet gears to distribute a single input into two mutually exclusive outputs, reducing coupling effects and providing a new grasping modality through belt-based traction. In this paper, we detail the structural design, kinematic and static analyses, and experimental validation of our manipulator, emphasizing the role of planet gears in achieving these functionalities.
The core innovation of our manipulator lies in the use of a planetary gear system where both the output shaft and the ring gear are not fixed, allowing for two distinct motion outputs. One output drives the rotation of the fingers for gripping, while the other enables infinite rotation of a pulley for belt-based pulling. This single-input, double-output configuration minimizes the dynamic coupling common in underactuated systems. Additionally, we incorporate a resistance torque adjustment mechanism that modulates the clamping force based on the angular displacement of a hollow gear, eliminating the need for external sensors. The manipulator’s three-fingered circular arrangement ensures stable grasping of both rigid and flexible objects, with the belt providing a compliant contact surface. Through extensive testing, we demonstrate the manipulator’s ability to adjust clamping force and successfully grasp various objects, validating the effectiveness of the planet gears-based design.
Structural Design of the Manipulator
The manipulator consists of two main components: the finger structure and the transmission system. Each finger is designed to perform both gripping and pulling actions, driven by a single motor through a planetary gear mechanism. The finger structure, as illustrated in the conceptual diagrams, includes two worm gears and worms that control the rotation of the first joint and the belt movement, respectively. Specifically, Worm 1 and Worm Gear 1 manage the rotation of Joint 1, which, through a parallelogram linkage, closes the gripping finger smoothly to grasp objects. Worm 2 and Worm Gear 2 transmit power to a gear system that drives the belt, enabling the pulling function. The use of worm gears provides self-locking capabilities, preventing the release of grasped objects when the motor is off and ensuring stability during pulling operations.
To address challenges in belt tension and support, we integrated two tensioning wheels connected by a spring. These wheels maintain adequate belt tension, prevent excessive deformation under load, and extend the belt’s lifespan by providing multiple support points. This design is crucial for handling objects of varying weights and sizes, as it ensures consistent performance without slippage or failure. The transmission system centers on the planetary gear mechanism, which distributes torque between the output shaft and the ring gear. The output shaft is connected to a coupling that drives the gripping motion via torque distribution gears, while the ring gear is fixed to a斜面力矩分配齿轮 (inclined torque distribution gear) that controls the belt rotation. The resistance torque adjustment mechanism, embedded between the output shaft and ring gear, allows for clamping force modulation by compressing a spring through the rotation of a hollow gear along a threaded tube. This mechanism converts angular displacement into a resistive force on the斜面力矩分配齿轮, thereby increasing the torque required to initiate the pulling motion.
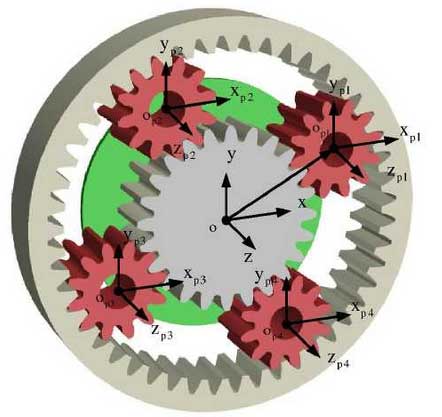
The planetary gear mechanism, with its planet gears, sun gear, and ring gear, enables the distribution of input torque based on resistance differences. When the motor is activated, the output shaft rotates first if its total resistance torque is lower than that of the ring gear, closing the fingers. Once the fingers grip an object, the resistance on the output shaft increases, causing the ring gear to rotate and drive the belt. This sequential operation ensures that gripping precedes pulling, enhancing the manipulator’s adaptability. The use of planet gears in this configuration allows for efficient torque splitting and reduces the complexity typically associated with underactuated systems. The overall design prioritizes simplicity, with a single motor controlling multiple functions through the strategic use of planet gears and mechanical linkages.
Kinematic and Static Analysis
To understand the manipulator’s behavior, we perform kinematic and static analyses. The three fingers are arranged in a circular pattern, and for simplicity, we analyze one finger in a planar coordinate system. Let the origin O be at Joint 1, with the X-axis horizontal and Y-axis vertical. The position of the fingertip P0 before contact is given by:
$$ \begin{bmatrix} P_{0x} \\ P_{0y} \end{bmatrix} = \begin{bmatrix} l_1 \cos \theta – l_2 \\ l_1 \sin \theta + l_4 \end{bmatrix} $$
where \( P_{0x} \) and \( P_{0y} \) are the coordinates, \( l_1 \) is the length from O to E, \( l_2 \) is from E to D, \( l_4 \) is from D to P0, and \( \theta \) is the rotation angle of Joint 1. The opening radius W of the three-fingered hand, assuming a circular distribution with radius R, is:
$$ W = P_{0x} + R = l_1 \cos \theta – l_2 + R $$
The velocity of the fingertip is derived by differentiating the position equation:
$$ \mathbf{V}_{P0} = \begin{bmatrix} -l_1 \sin \theta \\ l_1 \cos \theta \end{bmatrix} \dot{\theta} $$
After contact, the point P on the belt deforms by \( l_\Delta \) due to clamping force, and its coordinates become:
$$ \begin{bmatrix} P_x \\ P_y \end{bmatrix} = \begin{bmatrix} l_1 \cos \theta – l_2 + l_\Delta \\ l_1 \sin \theta + l \end{bmatrix} $$
where \( l \) is the distance from D to P during gripping. For static analysis, we apply the principle of virtual work to relate the input torque to the clamping force. When the finger grips an object, the equilibrium condition gives:
$$ \tau = F_x l_1 \sin \theta – F_y l_1 \cos \theta $$
Here, \( \tau \) is the input torque from the worm gear, \( F_x \) is the clamping force, and \( F_y \) is the vertical force, which for a three-fingered grip on an object of mass m is \( F_y = \frac{1}{3} mg \), with g as gravity. This equation highlights the dependence of clamping force on the joint angle and input torque, which is modulated by the planet gears system.
Resistance Torque Adjustment Mechanism Analysis
The resistance torque adjustment mechanism is key to achieving sensorless clamping force control. It operates by altering the resistance on the ring gear of the planetary gear system. The hollow gear, which is part of this mechanism, rotates and moves axially along a threaded tube, compressing a spring. The spring force \( F_s \) is given by:
$$ F_s = \phi \frac{p}{2\pi} k $$
where \( \phi \) is the angular displacement of the hollow gear, p is the lead of the threaded tube, and k is the spring constant. This force acts on a斜面力矩分配齿轮 (inclined torque distribution gear) through balls, generating a resistance torque \( T_{ad} \):
$$ T_{ad} = \frac{d}{2} F_s \tan \alpha = \phi \frac{p d k \tan \alpha}{4\pi} $$
Here, d is the diameter of the circle where the balls contact the斜面, and \( \alpha \) is the incline angle. The planetary gear system ensures that the input torque T from the motor is split such that \( T – T_{f0} = T_a = T_b \), where \( T_{f0} \) is the internal resistance of the planet gears, \( T_a \) is the torque on the output shaft, and \( T_b \) is on the ring gear. The total resistances are \( T_{af} = \sum T_{f1} + \tau \) for the output shaft and \( T_{cf} = \sum T_{f2} + T_{ad} + T_{sw} \) for the ring gear, where \( \sum T_{f1} \) and \( \sum T_{f2} \) are frictional losses, and \( T_{sw} \) is the belt torque. At the point of gripping, \( T_{af} = T_{cf} \), leading to:
$$ \tau = T_{ad} $$
Substituting into the static equation, the clamping force \( F_x \) becomes:
$$ F_x = \frac{T_{ad}}{l_1 \sin \theta} + \frac{1}{3} mg \cot \theta = \phi \frac{p d k \tan \alpha}{4\pi l_1} \frac{1}{\sin \theta} + \frac{1}{3} mg \cot \theta $$
Defining a torque adjustment coefficient \( K = \frac{p d k \tan \alpha}{4\pi l_1} \), we simplify to:
$$ F_x = \phi \frac{K}{\sin \theta} + \frac{1}{3} mg \cot \theta $$
This equation shows that the clamping force can be adjusted by varying the hollow gear’s angular displacement \( \phi \), independent of object size and weight within limits. The planet gears enable this by balancing the torques, and the mechanism allows for precise force control without electronic sensors.
Experimental Setup and Methods
We constructed a prototype using transparent acrylic and resin materials to visualize the power transmission. The resistance torque adjustment mechanism parameters are listed in Table 1.
| Symbol | Definition | Value |
|---|---|---|
| p | Lead of threaded tube | 1.5 mm |
| k | Spring constant | 0.5 N/mm |
| d | Contact circle diameter | 28 mm |
| α | Incline angle | 15° |
For clamping force testing, we used a cylindrical weight of mass 500 g, diameter 38 mm, and height 61 mm. A resistive film pressure sensor with a range of 0.5–20 N was attached to the object, and its output was converted to voltage via a dedicated module. Data acquisition was performed using an NI PXI system with LabVIEW software. To control the hollow gear’s angular displacement, we employed a reduction motor with an encoder and photoelectric switch, incrementing \( \phi \) by 60° steps and recording the clamping force. For grasping experiments, various objects were selected, as detailed in Table 2, to test the manipulator’s versatility with rigid and flexible materials.
| Object | Dimensions (mm×mm×mm) | Mass (g) | Material |
|---|---|---|---|
| Resin water bottle | 90×90×230 | 470 | Resin |
| Water bottle (full) | 64×64×227 | 520 | Plastic |
| Water bottle (empty) | 64×64×227 | 25 | Plastic |
| Iron cup | 66×66×220 | 275 | Iron |
| Paper roll | 104×104×93 | 125 | Fiber |
| Tape | 129×129×60 | 375 | Coated adhesive |
| Tissue | 129×80×40 | 95 | Fiber |
| Measuring tape | 95×100×40 | 270 | Plastic |
| Paper cup | 74×74×87 | 2 | Fiber |
| Ping pong ball | 40×40×40 | 2.7 | Celluloid |
| Weight | 38×38×61 | 500 | Iron |
| Scarf | 85×85×67 | 170 | Cotton |
Experimental Results and Discussion
The clamping force test results, plotted against hollow gear angular displacement, show a clear increasing trend. At \( \phi = 0^\circ \), the force is approximately 0.5 N, and at \( \phi = 900^\circ \), it reaches about 20 N. This demonstrates the effectiveness of the resistance torque adjustment mechanism in modulating clamping force through the planet gears system. The relationship is nearly linear, validating the derived equation \( F_x = \phi \frac{K}{\sin \theta} + \frac{1}{3} mg \cot \theta \). The use of planet gears allows for precise torque distribution, enabling this sensorless force control.
In grasping experiments, the manipulator successfully gripped and pulled all objects listed in Table 2. For rigid objects like the iron cup and weight, the manipulator applied sufficient clamping force without slippage, and the belt smoothly pulled them in. For flexible objects such as empty water bottles and paper cups, the adjustable clamping force prevented deformation or damage, showcasing the manipulator’s compliance. The planet gears ensured that gripping occurred before pulling, and the self-locking worm gears maintained hold without power. The belt’s infinite rotation avoided motor stall, enhancing durability. These results confirm that the planet gears-based design achieves reliable grasping and pulling with minimal coupling, as intended.
Conclusion
We have designed and validated an underactuated manipulator that uses a planetary gear mechanism to enable gripping and pulling functions with adjustable clamping force. The planet gears allow for a single input to drive two outputs, reducing dynamic coupling and simplifying control. The resistance torque adjustment mechanism provides sensorless force modulation, and the belt-based pulling offers a novel grasping mode. Experiments show effective clamping force adjustment from 1 N to 20 N and successful grasping of diverse objects. This design is particularly suited for mobile robots, where efficiency and adaptability are critical. Future work could explore optimization of the planet gears configuration for higher load capacity and integration with sensory feedback for enhanced autonomy.
