In the field of actuation systems, worm gears are widely employed for their ability to provide reverse self-locking, which isolates load disturbances from the input side. However, in vibration-prone environments, this self-locking feature can fail, leading to unintended movements in mechanisms such as valves. This study addresses the self-locking failure of a typical worm gear actuator during random vibration tests. Through detailed analysis, I identify the root causes and propose a magnetic stabilization mechanism to enhance self-locking under dynamic conditions. The improved design is validated via simulations and experiments, offering a reliable solution for actuators relying on worm gears in harsh environments.
Worm gears consist of a worm (similar to a screw) and a worm wheel, where the worm’s helical threads engage with the gear teeth. The self-locking property arises when the worm’s lead angle is less than or equal to the friction angle of the mating surfaces, preventing back-driving. In static conditions, this is straightforward, but vibrations introduce relative motions that reduce friction coefficients, compromising self-locking. My investigation focuses on a specific actuator where valve opening occurred unexpectedly during vibration tests, traced to worm gear self-locking failure. I explore the mechanics behind this, design an innovative magnetic solution, and verify its effectiveness.
The actuator in question includes a motor, worm, worm wheel, screw mechanism, and valve. Under power, the motor drives the worm to rotate the worm wheel, converting motion to linear action via a screw pair to open or close the valve. When unpowered, the worm gears should self-lock to hold the valve position against external loads. However, random vibration tests along the Y-axis revealed that the valve opened freely post-vibration, indicating self-locking breakdown. This paper delves into the factors affecting worm gear self-locking, presents a magnetic stabilization approach, and discusses results from analysis and testing.
Mechanism Overview and Functionality
Actuators utilizing worm gears are critical in applications requiring precise motion control and load isolation. The self-locking capability ensures that external forces cannot reverse-drive the system, providing safety and stability. In this study, the actuator’s worm gear transmission is central to its operation. The worm, driven by a motor, engages with the worm wheel to transmit torque, while a screw mechanism converts rotational motion to linear displacement for valve actuation. Under ideal conditions, the worm’s lead angle and the friction between surfaces maintain self-locking.
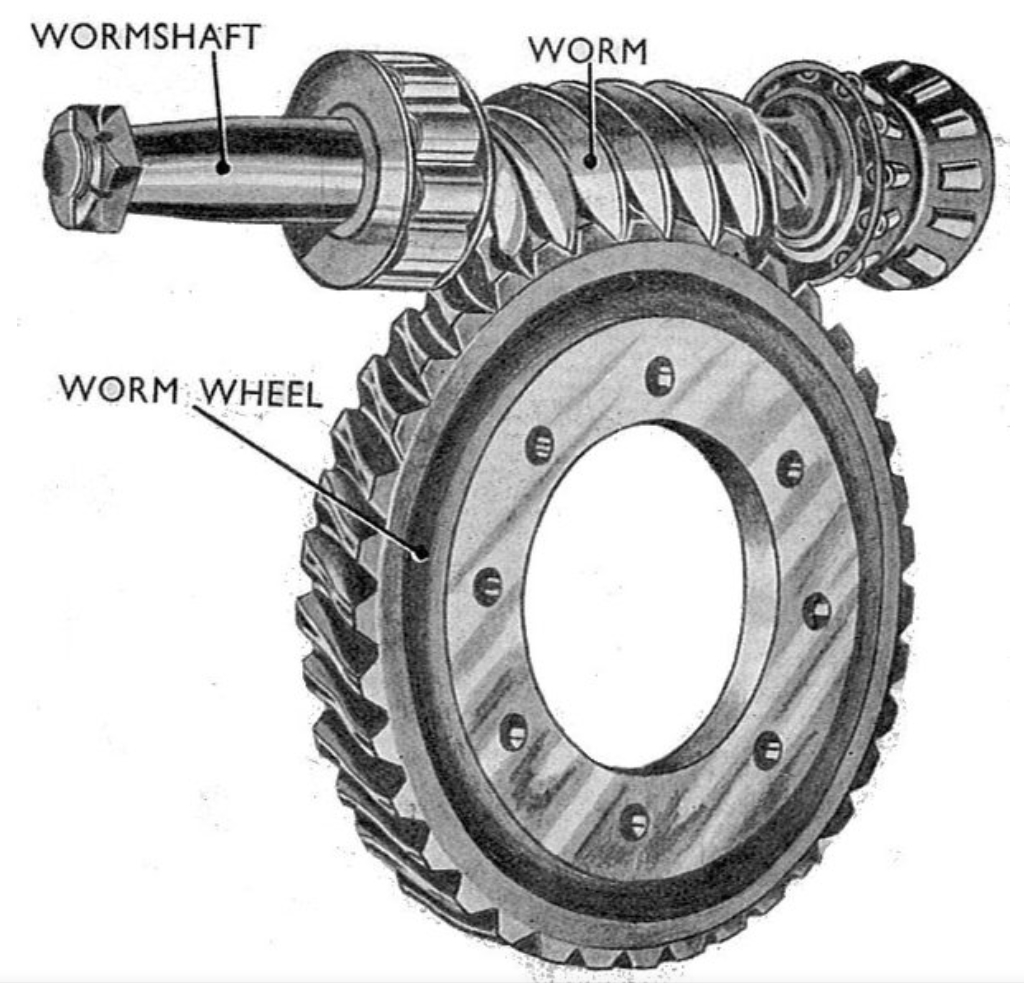
To understand the self-locking behavior, consider the forces at play. In a worm gear pair, the worm experiences tangential, radial, and axial forces. The self-locking condition can be modeled similarly to a block on an inclined plane, where the block represents the worm wheel and the plane the worm. For self-locking, the incline angle (analogous to the worm’s lead angle) must not exceed the friction angle. Mathematically, this is expressed as:
$$ \gamma \leq \beta $$
where $\gamma$ is the lead angle of the worm and $\beta$ is the friction angle. The friction angle depends on the coefficient of friction $f$ between the worm and worm wheel materials, given by $\beta = \arctan(f)$. Factors influencing $f$ include material pairing, surface finish, lubrication, and relative sliding velocity. For instance, higher sliding velocities reduce $f$, making self-locking harder to achieve. Tables 1 and 2 summarize key parameters for worm gears and friction coefficients under different conditions.
| Worm Characteristic Coefficient (q) | Lead Angle ($\gamma$) |
|---|---|
| 7.5 | 7°36′ |
| 8 | 7°08′ |
| 9 | 6°20′ |
| 10 | 5°43′ |
| 12 | 4°46′ |
| 16 | 3°35′ |
| Worm Material | Worm Wheel Material | Friction Coefficient (f) |
|---|---|---|
| Steel | Steel | 0.10–0.15 |
| Steel | Cast Iron | 0.10–0.30 |
| Steel | Brass | 0.03–0.15 |
| Steel | Bronze | 0.10–0.18 |
In vibration environments, the relative motion between the worm and worm wheel increases sliding velocity, lowering the friction coefficient. This reduction can cause $\beta$ to fall below $\gamma$, leading to self-locking failure. Additionally, imbalances in the motor rotor and worm assembly can generate rotational torques under vibration, further exacerbating the issue. For example, in the tested actuator, the free rotation torque of the worm was measured at approximately 1.65 mN·m during vibration, sufficient to overcome the diminished friction torque.
Analysis of Self-Locking Failure Under Vibration
The self-locking mechanism of worm gears relies on static friction, but vibrations induce dynamic conditions. When subjected to random vibrations, the worm and worm wheel experience oscillatory movements due to gaps in the meshing and unconstrained ends. This results in increased sliding velocities, which in turn reduce the effective friction coefficient. The relationship between sliding velocity $V_s$ and friction coefficient $f$ is critical; as $V_s$ rises, $f$ decreases. Table 3 illustrates this trend for steel-bronze pairs, common in worm gears.
| Sliding Velocity $V_s$ (m/s) | Friction Coefficient (f) |
|---|---|
| 0.010 | 0.110 |
| 0.100 | 0.080 |
| 1.000 | 0.045 |
| 5.000 | 0.022 |
| 10.000 | 0.016 |
| 15.000 | 0.014 |
| 24.000 | 0.013 |
Moreover, the distinction between static and dynamic friction coefficients plays a role. Dynamic friction coefficients are generally lower than static ones, as shown in Table 4. Under vibration, the transition to dynamic friction reduces the friction angle, potentially below the lead angle. For the actuator, the lead angle $\gamma$ was calculated based on the worm’s parameters. Using the formula for lead angle:
$$ \gamma = \arctan\left(\frac{Z_1}{q}\right) $$
where $Z_1$ is the number of starts (e.g., $Z_1 = 1$ for single-start worms) and $q$ is the worm characteristic coefficient. With $q = 10$, $\gamma \approx 5.71^\circ$. The friction angle $\beta$ for steel-bronze pairs can vary, but under vibration, $f$ may drop to 0.016, giving $\beta \approx 0.92^\circ$, which is less than $\gamma$. This imbalance causes self-locking to fail, allowing the worm to rotate and the valve to open.
| Material Pair | Static Friction Coefficient | Dynamic Friction Coefficient |
|---|---|---|
| Steel-Steel | 0.242 | 0.038–0.088 |
| Steel-Cast Iron | 0.330 | 0.074–0.273 |
Another factor contributing to rotation under vibration is rotor imbalance. The motor rotor and worm form a rotating assembly, and any mass asymmetry can generate torques when subjected to vibration. Even after balancing, residual imbalances persist, and in vibration, bearing resistances change, allowing rotation. In the actuator, this compounded the self-locking issue, necessitating a solution to stabilize the worm.
Innovative Magnetic Stabilization Design
To address the self-locking failure, I developed a magnetic stabilization mechanism that applies a continuous opposing torque to the worm, preventing rotation under vibration. This non-contact solution uses permanent magnets arranged to create a magnetic field that resists motion, enhancing the effective friction without adding mechanical wear. The design is inspired by magnetic coupling principles, where fixed and rotating magnetic arrays interact to transmit or resist torque.
The magnetic stabilization unit consists of a magnetic rotor fixed to the worm shaft and a stator with permanent magnets embedded in the actuator housing. As the worm attempts to rotate under vibration, the magnetic field generates a restoring torque. The key advantage is that it operates without physical contact, making it durable and suitable for high-vibration environments. The arrangement uses radially magnetized magnets spaced evenly around the circumference, ensuring that the magnetic force always opposes rotation, regardless of direction.
In this design, the magnetic rotor is rigidly connected to the worm, while the stator magnets are fixed. When the rotor moves, the magnetic interaction produces a torque that counteracts the vibration-induced rotation. The magnitude of this torque depends on the magnet strength, spacing, and alignment. For the actuator, I selected samarium-cobalt magnets for their high coercivity and temperature stability. The magnetic force can be modeled using electromagnetic theory, and the torque $T_m$ is approximately proportional to the square of the magnetic flux density and the number of magnet pairs.
To quantify the improvement, I derived equations for the magnetic torque. For a simplified model, the torque between two magnets can be expressed as:
$$ T_m = k \cdot B^2 \cdot A \cdot r \cdot \sin(\theta) $$
where $k$ is a constant, $B$ is the magnetic flux density, $A$ is the area of interaction, $r$ is the radius, and $\theta$ is the angular displacement. In the actual mechanism, with multiple magnets, the total torque sums vectorially. For the designed configuration with six magnets, the maximum torque was simulated to be around 4.54 mN·m, exceeding the vibration-induced torque of 1.65 mN·m, thus ensuring stability.
Simulation and Analytical Validation
I conducted finite element simulations to analyze the magnetic stabilization mechanism’s performance. The model included the magnetic rotor, stator, and surrounding air region, with materials defined for magnetic properties (e.g., samarium-cobalt magnets with remanence $B_r = 1.18$ T and coercivity $H_c = -880$ kA/m). Simulations were run for various rotation angles of the rotor (0°, 15°, 30°, 45°, and 60°) to assess torque and force variations.
The results showed that the axial magnetic force on individual magnets remained consistent, around 0.12 N per magnet, leading to a total axial force that followed a cosine-like pattern with angle. For instance, at 0° and 60°, the force peaked at approximately 1.27 N, while at 30°, it minimized near 0 N. The torque around the Z-axis (aligned with the worm shaft) exhibited a sinusoidal trend, with maximum torque of 4.54 mN·m at 30° and minimum at 0° and 60°. This torque profile confirms that the mechanism provides sufficient opposing moment to prevent worm rotation under vibration.
Mathematically, the torque variation can be approximated as:
$$ T_m(\theta) = T_{\text{max}} \cdot \sin(2\theta) $$
where $T_{\text{max}} = 4.54$ mN·m and $\theta$ is the rotation angle. This ensures that for any small displacement, a restoring torque is present. The simulation also considered power consumption implications. Based on motor characteristics, where rated torque (51 mN·m) corresponds to 3 A current, the additional 4.54 mN·m torque would increase current by about 0.26 A. Since the actuator’s operational current margin is 2 A, this is acceptable without affecting overall performance.
Experimental Verification and Results
To validate the design, I performed random vibration tests on the improved actuator along the Y-axis for 4 hours, replicating the conditions that previously caused self-locking failure. Post-vibration, the valve remained closed without power, demonstrating successful self-locking. Additionally, power-on tests showed a current increase of only 0.22 A, within tolerable limits, confirming that the magnetic stabilization does not significantly impact efficiency.
The experiments involved measuring worm rotation torque and valve position under vibration. With the magnetic mechanism, the worm’s free rotation was suppressed, and no unintended valve movements occurred. This aligns with simulation predictions and underscores the reliability of the approach. Compared to traditional methods like increasing friction through surface treatments or pre-loading, the magnetic solution offers a maintenance-free alternative with consistent performance.
Key Technologies and Applications
The magnetic stabilization mechanism represents a novel approach to enhancing worm gear self-locking in dynamic environments. Its key features include compact size, non-contact operation, and adaptability to various actuator designs. By using alternating magnet polarities, the torque always opposes motion, providing robust stability. This technology can be extended to other precision mechanisms requiring vibration resistance, such as aerospace actuators, robotic joints, and automotive systems.
Moreover, the design avoids common pitfalls like wear and tear, as no physical brakes or clutches are involved. The use of high-energy magnets ensures long-term reliability even in extreme conditions. For worm gears in general, this study highlights the importance of considering dynamic friction effects and offers a practical solution to maintain self-locking integrity.
Conclusion
In this study, I investigated the self-locking failure of worm gears under vibration and developed a magnetic stabilization mechanism to mitigate the issue. Through analysis, I identified that reduced friction coefficients due to sliding motions and rotor imbalances cause self-locking to fail. The proposed design uses permanent magnets to generate an opposing torque, proven effective via simulations and experiments. This improvement ensures reliable actuator performance in vibration-prone settings, with minimal impact on power consumption. The findings provide valuable insights for designing worm gear-based systems, emphasizing the need for dynamic stability considerations. Future work could explore optimized magnet configurations for higher torque capacities or integration with smart materials for adaptive control.
Overall, worm gears remain indispensable in actuation systems, and enhancing their self-locking capability under vibration expands their applicability across industries. The magnetic approach demonstrated here offers a scalable and efficient solution, paving the way for more resilient mechanical designs.
