In my decades of experience in mechanical engineering and gear design, I have consistently found hypoid gears to be one of the most intriguing and complex components in power transmission systems. The unique geometry of a hypoid gear, which allows for non-intersecting, offset axes between the pinion and the gear, presents both significant advantages and formidable challenges. Throughout this article, I will delve deep into the principles, design methodologies, manufacturing nuances, and applications of hypoid gears, drawing from my hands-on work and theoretical studies. The term “hypoid gear” will be central to our discussion, as understanding its intricacies is key to advancing modern machinery.
The fundamental concept of a hypoid gear stems from the evolution of bevel gears. While spiral bevel gears have intersecting axes, the hypoid gear introduces an offset, typically allowing the pinion to be mounted lower or higher than the gear center. This offset, often denoted as \( E \), is a critical parameter that influences the gear’s performance and design. The basic geometry can be described using coordinate transformations and surface equations. For instance, the tooth surface of a hypoid gear can be modeled as a ruled surface generated by the motion of a cutting tool. The mathematical representation often starts with the equation of a hyperboloid, which is the pitch surface. The relationship between the pinion and gear in a hypoid gear set is governed by the following kinematic condition:
$$ \omega_p / \omega_g = N_g / N_p $$
where \( \omega_p \) and \( \omega_g \) are the angular velocities of the pinion and gear, respectively, and \( N_p \) and \( N_g \) are their tooth numbers. The offset \( E \) modifies the traditional bevel gear equations, leading to more complex contact patterns. In my analysis, I frequently use the following set of design parameters for a hypoid gear, which are essential for defining its geometry:
| Parameter | Symbol | Typical Range | Description |
|---|---|---|---|
| Offset Distance | \( E \) | 10-100 mm | Perpendicular distance between axes |
| Pinion Tooth Count | \( N_p \) | 5-15 | Number of teeth on the pinion |
| Gear Tooth Count | \( N_g \) | 20-50 | Number of teeth on the gear |
| Mean Spiral Angle | \( \beta_m \) | 30°-50° | Angle of tooth curvature at pitch cone |
| Pressure Angle | \( \alpha \) | 20°-25° | Angle between tooth profile and tangent |
| Pitch Diameter (Gear) | \( D_g \) | 50-300 mm | Diameter at the pitch cone |
Designing a hypoid gear requires meticulous attention to tooth contact analysis (TCA) and stress calculations. The bending stress at the root of a hypoid gear tooth can be estimated using a modified Lewis formula, which I often apply in preliminary designs:
$$ \sigma_b = \frac{W_t \cdot K_a \cdot K_m}{b \cdot m_n \cdot Y} $$
where \( \sigma_b \) is the bending stress, \( W_t \) is the tangential load, \( K_a \) is the application factor, \( K_m \) is the load distribution factor, \( b \) is the face width, \( m_n \) is the normal module, and \( Y \) is the Lewis form factor. For hypoid gears, the form factor \( Y \) is more complex due to the curved teeth and offset, often requiring finite element analysis (FEA) for accurate results. Contact stress, crucial for pitting resistance, is given by the Hertzian contact theory. The maximum contact pressure \( p_{max} \) for a hypoid gear pair can be expressed as:
$$ p_{max} = \sqrt{\frac{W_t \cdot E^*}{\pi \cdot b \cdot \rho_{eq}}} $$
Here, \( E^* \) is the equivalent Young’s modulus, and \( \rho_{eq} \) is the equivalent radius of curvature at the contact point. For a hypoid gear, \( \rho_{eq} \) varies along the tooth profile, making iterative calculations necessary. In my practice, I use specialized software to simulate these stresses, but understanding the underlying formulas is vital for troubleshooting. The performance of a hypoid gear is highly dependent on proper lubrication and alignment, which I will discuss later.
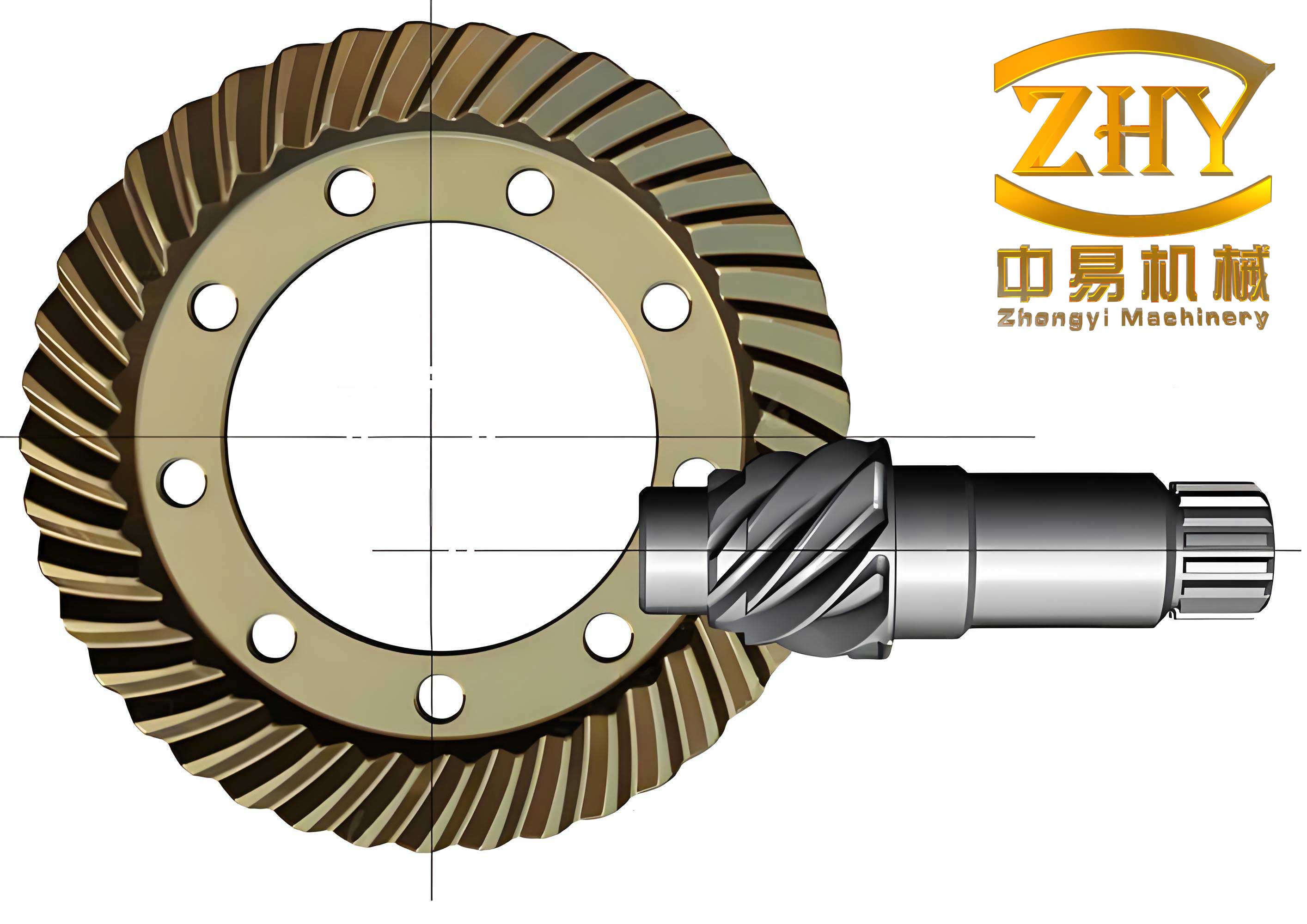
Manufacturing hypoid gears is a sophisticated process that I have overseen in various production facilities. The most common method is face milling or face hobbing using dedicated hypoid gear generators. The cutter head geometry must match the desired tooth form, and the machine settings are derived from the design parameters. For instance, the machine root angle \( \gamma \) and sliding base setting \( \Delta X \) are calculated based on the offset \( E \) and spiral angle \( \beta_m \). A key equation in setting up the generator is the ratio of roll, which controls the tooth curvature:
$$ R_r = \frac{N_c}{N_g} $$
where \( N_c \) is the number of cutter head blades and \( N_g \) is the gear tooth count. After cutting, hypoid gears often undergo heat treatment like carburizing and grinding to achieve high surface hardness and precision. The table below summarizes typical manufacturing steps and their purposes for a hypoid gear, based on my observations:
| Manufacturing Step | Key Parameters | Purpose | Challenges |
|---|---|---|---|
| Soft Cutting | Cutter diameter, blade angle | Rough tooth formation | Achieving correct tooth depth |
| Heat Treatment | Temperature, time | Increase hardness and wear resistance | Controlling distortion |
| Hard Finishing (Grinding) | Grinding wheel profile, feed rate | Final tooth geometry and surface finish | Maintaining accuracy under thermal effects |
| Inspection | Coordinate measuring machine (CMM) data | Verify dimensions and contact pattern | Aligning gear for measurement |
The applications of hypoid gears are vast, and I have seen them deployed in automotive differentials, industrial machinery, and aerospace systems. Their ability to transmit high torque with smooth operation due to the gradual tooth engagement makes them ideal for rear axle drives in vehicles. In automotive contexts, the hypoid gear set often operates with a high offset, allowing for a lower propeller shaft and thus a reduced vehicle floor height. This design advantage is quantified by the offset ratio, which I define as \( E / D_g \), typically ranging from 0.1 to 0.3. The efficiency of a hypoid gear drive is influenced by sliding velocities, which can be analyzed using the following formula for sliding velocity \( V_s \) at a point on the tooth surface:
$$ V_s = V_{1t} – V_{2t} $$
where \( V_{1t} \) and \( V_{2t} \) are the tangential velocities of the pinion and gear at that point. For a hypoid gear, the sliding is more pronounced than in spiral bevel gears, leading to higher heat generation but also better lapping-in during run-in. To optimize performance, I always recommend thorough testing under loaded conditions. The table below compares hypoid gears with other gear types based on my experience, highlighting why hypoid gears are preferred in certain scenarios:
| Gear Type | Axes Configuration | Typical Efficiency | Common Applications | Relative Cost |
|---|---|---|---|---|
| Hypoid Gear | Non-intersecting, offset | 92-96% | Automotive differentials, heavy trucks | High |
| Spiral Bevel Gear | Intersecting | 94-98% | Industrial drives, helicopters | Medium |
| Worm Gear | Non-intersecting, perpendicular | 50-90% | Low-speed, high-ratio drives | Low to Medium |
| Helical Gear | Parallel | 96-99% | General machinery, transmissions | Low |
In the design phase, one must consider the dynamic behavior of hypoid gears. Noise and vibration are critical issues, especially in automotive applications. From my research, the meshing frequency \( f_m \) of a hypoid gear pair is given by:
$$ f_m = \frac{N_p \cdot \omega_p}{60} = \frac{N_g \cdot \omega_g}{60} $$
where frequencies are in Hz. Excitation at this frequency and its harmonics can lead to noise if not damped properly. I often use finite element analysis to model the modal characteristics of a hypoid gear, but simplified analytical models can provide insights. For instance, the natural frequency \( f_n \) of a gear body can be approximated using Dunkerley’s method for a rotating disk:
$$ \frac{1}{f_n^2} \approx \frac{1}{f_b^2} + \frac{1}{f_s^2} $$
with \( f_b \) and \( f_s \) as bending and shear frequencies, respectively. Lubrication is another area where I have spent considerable effort. The film thickness \( h \) in an elastohydrodynamic lubrication (EHL) contact for a hypoid gear can be estimated by the Dowson-Higginson equation:
$$ h_{min} = 2.65 \cdot R^{0.43} \cdot (\alpha E’)^{0.54} \cdot \left( \frac{\eta_0 u}{E’ R} \right)^{0.7} \cdot W^{-0.13} $$
Here, \( R \) is the effective radius, \( \alpha \) is the pressure-viscosity coefficient, \( E’ \) is the reduced modulus, \( \eta_0 \) is the dynamic viscosity, \( u \) is the entraining velocity, and \( W \) is the load per unit width. Proper lubrication ensures longevity of the hypoid gear by reducing wear and friction.
The material selection for hypoid gears is paramount. In my projects, I commonly use case-hardened steels such as AISI 8620 or 9310 for high-stress applications. The core toughness and surface hardness are balanced through controlled heat treatment. The allowable bending stress \( \sigma_{all} \) for such materials can be derived from fatigue data, often expressed as:
$$ \sigma_{all} = \frac{S_{ut}}{N_f \cdot K_f} $$
where \( S_{ut} \) is the ultimate tensile strength, \( N_f \) is the safety factor, and \( K_f \) is the fatigue stress concentration factor. For hypoid gears, \( K_f \) is influenced by tooth fillet radius and surface finish. I have compiled typical material properties in the table below, which I reference during design reviews:
| Material Grade | Core Hardness (HRC) | Surface Hardness (HRC) | Fatigue Limit (MPa) | Typical Use in Hypoid Gears |
|---|---|---|---|---|
| AISI 8620 | 28-32 | 58-62 | 550-650 | Passenger car differentials |
| AISI 9310 | 32-36 | 60-64 | 600-700 | Aerospace and racing applications |
| SAE 4140 | 25-30 | 50-55 | 450-550 | Industrial heavy-duty drives |
| Case Carburized Steel | 30-35 | 58-63 | 580-680 | General hypoid gear sets |
Advancements in simulation technology have revolutionized hypoid gear design. I regularly employ multi-body dynamics software to analyze the entire drivetrain, incorporating hypoid gear models with flexible bodies. The equations of motion for a hypoid gear pair can be written in matrix form, considering degrees of freedom for rotation and translation:
$$ \mathbf{M} \ddot{\mathbf{q}} + \mathbf{C} \dot{\mathbf{q}} + \mathbf{K} \mathbf{q} = \mathbf{F}(t) $$
where \( \mathbf{M} \), \( \mathbf{C} \), and \( \mathbf{K} \) are mass, damping, and stiffness matrices, \( \mathbf{q} \) is the displacement vector, and \( \mathbf{F}(t) \) is the force vector including meshing forces. Solving this system helps predict dynamic loads and noise. Furthermore, topological optimization of hypoid gear teeth is an area I am exploring, using algorithms to minimize weight while maintaining strength. The objective function might be:
$$ \min \left( \int_V \rho \, dV \right) \text{ subject to } \sigma_{max} \leq \sigma_{allowable} $$
where \( \rho \) is density and \( V \) is volume. These computational tools allow for rapid prototyping of hypoid gear designs, though physical testing remains indispensable.
In terms of failure modes, I have observed that hypoid gears are prone to pitting, scuffing, and tooth breakage if not properly designed. Pitting life can be estimated using the Ioannides-Harris equation based on subsurface stress fields:
$$ L_{10} = \left( \frac{C}{\tau_{max}} \right)^m $$
with \( L_{10} \) as the life at 90% reliability, \( C \) as a material constant, \( \tau_{max} \) as the maximum shear stress, and \( m \) as the Weibull slope. For hypoid gears, the stress history is multiaxial, requiring careful analysis. Scuffing, or adhesive wear, is mitigated by selecting appropriate lubricants with extreme pressure (EP) additives. The flash temperature criterion, often used, calculates the instantaneous temperature rise \( \Delta T \) at the contact:
$$ \Delta T = \frac{f \cdot W_t \cdot V_s}{J \cdot b \cdot \sqrt{\pi \cdot \kappa \cdot t}} $$
where \( f \) is the coefficient of friction, \( J \) is the mechanical equivalent of heat, \( \kappa \) is the thermal diffusivity, and \( t \) is the time of contact. Keeping \( \Delta T \) below a critical value prevents scuffing in hypoid gears.
Looking to the future, I believe hypoid gears will continue to evolve with trends like electrification and lightweighting. In electric vehicles, hypoid gears are used in reducers for their compactness and high torque capacity. The demand for higher efficiency drives research into low-friction coatings and improved surface finishes. From my perspective, the integration of hypoid gears with advanced sensors for condition monitoring is a promising development. Vibration signatures can be analyzed using fast Fourier transforms (FFT) to detect wear early:
$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2\pi f t} dt $$
where \( x(t) \) is the time-domain vibration signal and \( X(f) \) is its frequency spectrum. Anomalies in the spectrum near the meshing frequency often indicate issues with the hypoid gear mesh.
To summarize, the design and application of hypoid gears involve a multidisciplinary approach blending geometry, mechanics, materials science, and manufacturing. Throughout my career, I have emphasized the importance of iterative design and validation. The key formulas and tables presented here are tools I use daily to ensure reliability and performance. Whether for automotive, industrial, or aerospace use, the hypoid gear remains a cornerstone of power transmission, and its optimization is a continuous journey. I encourage engineers to deepen their understanding of hypoid gear principles, as mastering them unlocks solutions for demanding mechanical systems.
In conclusion, my firsthand experience with hypoid gears has taught me that success lies in attention to detail—from initial parameter selection to final quality control. The mathematical models, such as those for stress and dynamics, provide a foundation, but practical insights from testing are irreplaceable. As technology advances, I anticipate further innovations in hypoid gear design, perhaps through additive manufacturing or AI-driven optimization. For now, the hypoid gear stands as a testament to engineering ingenuity, and I am excited to see its future developments.
