In the realm of mechanical transmissions, the pursuit of compact, efficient, and high-ratio drives has always been a focal point for engineers and researchers. I have long been fascinated by the unique characteristics of spiral bevel gears and their potential beyond traditional cross-axis applications. Spiral bevel gears are renowned for their high overlap ratio, superior strength, smooth operation, and low noise, making them staples in automotive, aerospace, marine, and machine tool industries. Concurrently, planetary gear transmissions with small teeth difference offer remarkable advantages such as power splitting, coaxial input and output shafts, and high transmission ratios. However, a review of existing literature reveals a significant gap: the integration of spiral bevel gears into planetary drives with small teeth difference remains unexplored. In this article, I propose and analyze a novel transmission system that combines spiral bevel gears with small teeth difference planetary mechanisms. This innovative approach aims to achieve a drive that is not only compact and lightweight but also capable of delivering high efficiency and a wide range of transmission ratios. I will delve into the principles, derive key formulas for transmission ratio and efficiency, and provide extensive analysis supported by tables and mathematical models. The goal is to establish a foundational framework for designing such transmissions, potentially revolutionizing applications in areas like wind turbine gearboxes where space and performance are critical.
The core idea stems from challenging the conventional notion that spiral bevel gears are limited to intersecting shaft configurations. By incorporating them into a planetary arrangement with small teeth difference, I demonstrate that coaxial or parallel shaft transmission becomes feasible. This synergy leverages the strengths of both technologies: the robustness and smoothness of spiral bevel gears and the compactness and ratio flexibility of planetary drives. Throughout this discussion, I will repeatedly emphasize the role of spiral bevel gears as the enablers of this novel architecture. Their curved teeth and gradual engagement are pivotal in managing the dynamic loads within the planetary setup. To visualize the typical structure of a spiral bevel gear, consider the following image, which illustrates the intricate tooth geometry that contributes to its performance. This image serves as a reference for understanding the components involved in the proposed system.
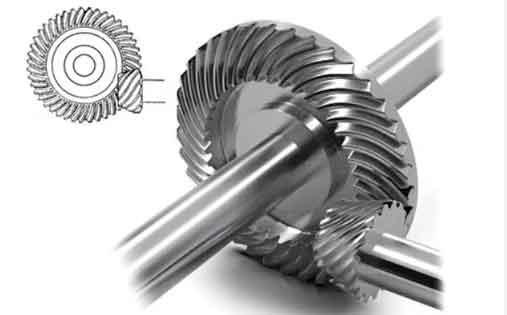
I begin by detailing the transmission principle. The proposed spiral bevel gear planetary drive with small teeth difference is essentially a 2K-H type planetary mechanism. It comprises four spiral bevel gears: two central gears (often referred to as sun gears) and two planet gears. In the basic configuration, gear 1 is the input, integrated with the input shaft; gears 2 and 3 are planet gears mounted on a common carrier H, which serves as the output shaft; and gear 4 is fixed to the housing. The key innovation lies in the arrangement: all gears are spiral bevel gears, but through careful design of shaft angles (typically set to a specific angle Σ), the system achieves coaxial alignment of the input and output shafts. The “small teeth difference” refers to the integer difference between the tooth counts of the two central gears (N1 and N4), usually 1, 2, 3, or 4. When N1 > N4, the system acts as a speed increaser; when N1 < N4, it functions as a speed reducer. For this analysis, I focus on the speed-increasing mode to elucidate the principles.
During operation, as gear 1 rotates, it drives planet gear 2. Since gear 2 is connected to carrier H, it undergoes both rotation (spin) and revolution (orbit) around gear 1. Because gears 2 and 3 are on the same shaft, they share the same rotational speed. Gear 3, in turn, meshes with fixed gear 4, causing further motion that drives carrier H. The result is an output through carrier H with a significantly higher speed than the input. The use of spiral bevel gears ensures that the meshing is smooth and can handle the complex motions inherent in planetary systems. The table below summarizes the component roles and motions in this configuration.
| Component | Role | Motion Description | Tooth Count Symbol |
|---|---|---|---|
| Gear 1 | Input Sun Gear | Active rotation, drives planet gear 2 | N1 |
| Gear 2 | Planet Gear | Rotates and revolves, meshes with gear 1 | N2 |
| Gear 3 | Planet Gear | Rotates and revolves, meshes with gear 4 | N3 |
| Gear 4 | Fixed Sun Gear | Stationary, reaction element | N4 |
| Carrier H | Output Carrier | Output shaft, carries planet gears 2 and 3 | – |
The transmission ratio is a critical parameter for any gear system. To derive the ratio for this spiral bevel gear planetary drive, I employ the relative velocity method (also known as the fixed carrier method). Denote the speeds of gears 1, 2, 3, 4, and carrier H as n1, n2, n3, n4, and nH, respectively. Since gears 2 and 3 are rigidly connected, n2 = n3. For the speed-increasing case, gear 4 is fixed, so n4 = 0. The transmission ratio from input (gear 1) to output (carrier H) is defined as i_{4H1} = nH / n1. By analyzing the relative motions in the planetary train, I obtain the fundamental relationship for the conversion ratio in the inverted mechanism:
$$ i_{14}^{H} = \frac{n_1 – n_H}{n_4 – n_H} = \frac{N_2 N_4}{N_1 N_3} $$
Substituting n4 = 0 and solving for i_{4H1} yields:
$$ i_{4H1} = \frac{n_H}{n_1} = \frac{1}{1 – \frac{N_2 N_4}{N_1 N_3}} = \frac{N_1 N_3}{N_1 N_3 – N_2 N_4} $$
This formula highlights the flexibility of the system. By adjusting the tooth counts of the spiral bevel gears, a wide range of transmission ratios can be achieved. Notably, when the planet gears have equal tooth counts (N2 = N3), the expression simplifies to:
$$ i_{4H1} = \frac{N_1}{N_1 – N_4} $$
This simplified form clearly shows that the transmission ratio depends inversely on the teeth difference (N1 – N4). A smaller difference results in a larger ratio, which is a hallmark of small teeth difference drives. To illustrate, I present a table comparing different tooth count combinations and their resulting transmission ratios. This demonstrates the capability of spiral bevel gears in achieving high ratios within a compact space.
| Case | N1 | N2 = N3 | N4 | Teeth Difference (N1 – N4) | Transmission Ratio i_{4H1} |
|---|---|---|---|---|---|
| A | 43 | 11 | 41 | 2 | 21.5 |
| B | 50 | 15 | 48 | 2 | 25.0 |
| C | 30 | 10 | 28 | 2 | 15.0 |
| D | 43 | 11 | 40 | 3 | 14.33 |
| E | 100 | 20 | 99 | 1 | 100.0 |
The table underscores that with spiral bevel gears, even a single tooth difference can yield ratios up to 100:1, showcasing the system’s potential for high-ratio applications. Moreover, compared to traditional planetary gears like the 2K-H type with spur gears, which often require multiple stages for high ratios, this spiral bevel gear configuration achieves similar or higher ratios in a simpler two-stage meshing arrangement. For instance, a conventional planetary with N1=15, N2=12, N3=45, and three planets (k=3) gives i = 1 + N3/N1 = 4, far lower than the ratios achievable with spiral bevel gears in small teeth difference setups.
Beyond the transmission ratio, efficiency is paramount for practical adoption. The efficiency of spiral bevel gear planetary drives with small teeth difference is influenced by several factors, including gear mesh losses, bearing friction, lubrication churning, and load-sharing mechanisms. I derive the efficiency formula focusing on the gear mesh losses in the planetary train. Let η^{(H)} denote the mesh efficiency of the converted mechanism (where carrier H is fixed), which accounts for the combined losses from the two meshing pairs: gear 1-2 and gear 3-4. For spiral bevel gears, typical single-pair mesh efficiency is around 0.985 to 0.99, so for two pairs, η^{(H)} ≈ (0.985)^2 = 0.970225. The input power is P_in = M1 ω1, and the output power is P_out = -M_H ω_H, where M1 and M_H are torques, and ω1 and ω_H are angular velocities. The power loss in the converted mechanism is related to the loss in relative motion. After detailed derivation considering the power flow and loss mechanisms, the transmission efficiency η_{4H1} from input gear 1 to output carrier H is given by:
$$ \eta_{4H1} = \frac{1}{1 + (1 – \eta^{(H)}) \cdot i_{4H1}} $$
This equation reveals that efficiency decreases as the transmission ratio increases, which is a common trait in high-ratio planetary drives. For the case where N1=43, N2=N3=11, N4=41, i_{4H1}=21.5, and η^{(H)}=0.970225, the efficiency calculates to:
$$ \eta_{4H1} = \frac{1}{1 + 21.5 \times (1 – 0.970225)} \approx 0.6097 \text{ or } 60.97\% $$
While this may seem low, it’s important to note that this accounts only for mesh losses. In practice, overall efficiency will be higher when considering other factors, but the trend remains. To achieve both high ratio and acceptable efficiency, I propose using multi-stage configurations. For example, two identical stages with i=6.14 each (from N1=43, N4=36, N2=N3=11) yield a total ratio of 37.7 and a combined efficiency of (0.8454)^2 ≈ 0.7147 or 71.47%, which is more favorable. Below is a table showing efficiency variations with different tooth counts and stages, emphasizing the trade-offs involved in designing with spiral bevel gears.
| Configuration | N1, N4 (Diff) | N2=N3 | Single-Stage Ratio i | Single-Stage Efficiency η (%) | Two-Stage Total Ratio | Two-Stage Total Efficiency (%) |
|---|---|---|---|---|---|---|
| Config 1 | 43, 41 (2) | 11 | 21.5 | 60.97 | 462.25 | 37.17 |
| Config 2 | 43, 36 (7) | 11 | 6.14 | 84.54 | 37.70 | 71.47 |
| Config 3 | 50, 48 (2) | 15 | 25.0 | 58.42 | 625.0 | 34.13 |
| Config 4 | 30, 28 (2) | 10 | 15.0 | 68.18 | 225.0 | 46.49 |
The efficiency analysis must also consider directional aspects. From the ratio formula, when N1N3 > N2N4, the input and output shafts rotate in the same direction, which is assumed in the above derivations. For the opposite case (N1N3 < N2N4), the shafts rotate oppositely, and the efficiency formula requires adjustment, but the methodology remains similar. I have focused on the same-direction case for clarity, but designers must account for this in applications.
To deepen the understanding, I explore the mechanical design considerations for spiral bevel gears in this planetary context. The tooth geometry of spiral bevel gears involves complex parameters such as spiral angle, pressure angle, and face width. These parameters must be optimized to ensure proper meshing under the combined spin and orbit motions. For instance, the spiral angle, typically between 20° and 35°, influences the smoothness of engagement and load capacity. In planetary drives, dynamic loads can be higher due to the orbiting motion, so spiral bevel gears with higher overlap ratios are advantageous. I recommend using Gleason or Klingelnberg systems for designing these gears, ensuring conjugate tooth profiles that minimize sliding and wear. The formula for the normal module m_n relates to the axial forces, and for spiral bevel gears, the equivalent number of teeth Z_v is given by:
$$ Z_v = \frac{Z}{\cos^3 \beta} $$
where Z is the actual tooth count and β is the spiral angle. This affects bending strength calculations. Additionally, the shaft angle Σ must be precisely set to achieve coaxiality; in most designs, Σ is chosen so that the axes of gears 1 and 4 align with carrier H. A common approach is to use Σ = 90° for orthogonal arrangements, but non-right angles can be used for compact packaging.
Load distribution is another critical aspect. In planetary systems, load sharing among planet gears is vital for durability. For spiral bevel gear planets, due to their stiffness and precision, load sharing can be achieved through flexible pinions or floating carriers. I suggest using a floating carrier H to self-align and distribute loads evenly, which is common in small teeth difference drives. The tangential force F_t on a spiral bevel gear tooth can be estimated from the torque and pitch radius:
$$ F_t = \frac{2T}{d_m} $$
where T is the torque and d_m is the mean pitch diameter. For spiral bevel gears, d_m depends on the cone distance and face width. These forces must be analyzed in the planetary context to size bearings and shafts appropriately.
Now, let’s consider practical applications and benefits. The integration of spiral bevel gears into small teeth difference planetary drives opens doors for industries requiring high power density. Wind turbine gearboxes are a prime example, where space constraints and high torque demands exist. Traditional parallel-stage gearboxes are bulky, whereas this spiral bevel gear planetary system can offer a compact coaxial solution with high speed-up ratios from the low-speed rotor to the generator. Similarly, in aerospace actuators or robotic joints, the compactness and high ratio can reduce weight and improve performance. The smooth operation of spiral bevel gears also contributes to lower noise and vibration, which is crucial in consumer automotive transmissions or precision machinery.
To further illustrate the design flexibility, I present a comprehensive table comparing this spiral bevel gear planetary drive with conventional planetary drives and traditional spiral bevel gear pairs. This highlights the unique advantages brought by the fusion of these technologies.
| Feature | Traditional Spiral Bevel Gear Pair | Conventional Planetary Drive (Spur Gears) | Spiral Bevel Gear Small Teeth Difference Planetary Drive |
|---|---|---|---|
| Shaft Configuration | Intersecting axes (usually 90°) | Coaxial or parallel axes | Coaxial axes achieved via planetary arrangement |
| Transmission Ratio Range | Limited, typically 1:1 to 10:1 | Moderate, up to 100:1 with multiple stages | High, up to 100:1 or more in single stage |
| Compactness | Moderate, requires space for shaft angles | Good, but multiple planets add complexity | Excellent, minimal components (4 gears, 1 carrier) |
| Efficiency | High (95-98%) | High (90-97%) but drops with high ratios | Moderate to high, depends on ratio and design |
| Noise and Vibration | Low due to gradual engagement | Can be high, especially at high speeds | Low, benefits from spiral bevel gear smoothness |
| Load Capacity | High, good for heavy loads | High through load sharing | High, combines strength of spiral bevel gears and planetary load distribution |
In terms of manufacturing, spiral bevel gears require specialized equipment like spiral bevel gear generators (e.g., Gleason machines), which can increase cost. However, for high-performance applications, this investment is justified. For the planetary setup, assembly precision is key to ensure proper meshing of all spiral bevel gears. I recommend using computer-aided design (CAD) and finite element analysis (FEA) to simulate the tooth contacts and optimize the geometry for minimal stress concentrations.
Looking ahead, research opportunities abound. Future work could explore the dynamic behavior of spiral bevel gears in planetary motion, including vibration modes and thermal effects. Experimental validation through prototypes is essential to confirm the theoretical efficiency and durability. Additionally, material advancements, such as using composite materials or advanced surface treatments for spiral bevel gears, could further enhance performance. The potential for integrating this transmission into electric vehicle drivetrains or industrial robotics warrants investigation, given the demand for efficient, compact power transmission solutions.
In conclusion, I have presented a thorough analysis of applying spiral bevel gears in planetary drives with small teeth difference. This novel configuration breaks the traditional barrier of spiral bevel gears being limited to intersecting shafts, enabling coaxial high-ratio transmissions. Through detailed derivations, I established formulas for transmission ratio and efficiency, demonstrating that spiral bevel gears can achieve ratios exceeding 20:1 in a single stage, albeit with an efficiency trade-off that can be mitigated via multi-stage designs. The use of tables and mathematical models underscores the design flexibility and performance characteristics. Spiral bevel gears, with their inherent smoothness and strength, are pivotal in making this system viable for demanding applications like wind energy, aerospace, and precision machinery. I believe this work lays a foundation for further development and optimization, potentially leading to next-generation compact gearboxes that leverage the best of both spiral bevel and planetary technologies. As the push for miniaturization and efficiency continues, innovations like this spiral bevel gear planetary drive will play a crucial role in advancing mechanical transmission systems worldwide.
