The pursuit of efficient, compact, and reliable power transmission has long driven innovation in gear design. Among the various solutions, screw gears, particularly worm gears, hold a distinguished position. They offer unparalleled advantages in terms of high single-stage reduction ratios, inherent self-locking capability, smooth and quiet operation due to their sliding contact, and a remarkably compact layout. However, traditional cylindrical worm drives with straight or involute profiles are often hampered by relatively low transmission efficiency and limited load capacity due to concentrated contact stresses. This has led to the development of advanced geometries aimed at improving these performance metrics. One of the most significant advancements in this field is the torus envelope worm gear, internationally known as the ZC1 type. This design represents a paradigm shift from the conventional generating process, resulting in a concave-convex tooth contact that dramatically enhances load distribution and lubrication conditions. This article, based on principles of gearing and numerical analysis, delves into a comprehensive investigation of the meshing characteristics of the ZC1 screw gear set. The primary focus is on analyzing the meshing zone and its boundaries while quantitatively assessing the influence of critical design parameters—namely, the pressure angle ($\alpha$), the profile arc radius ($\rho$), and the profile shift coefficient ($x$)—on the effective contact area and the onset of undercutting. The goal is to establish clear parametric relationships that can inform optimal design strategies for these highly efficient screw gears.
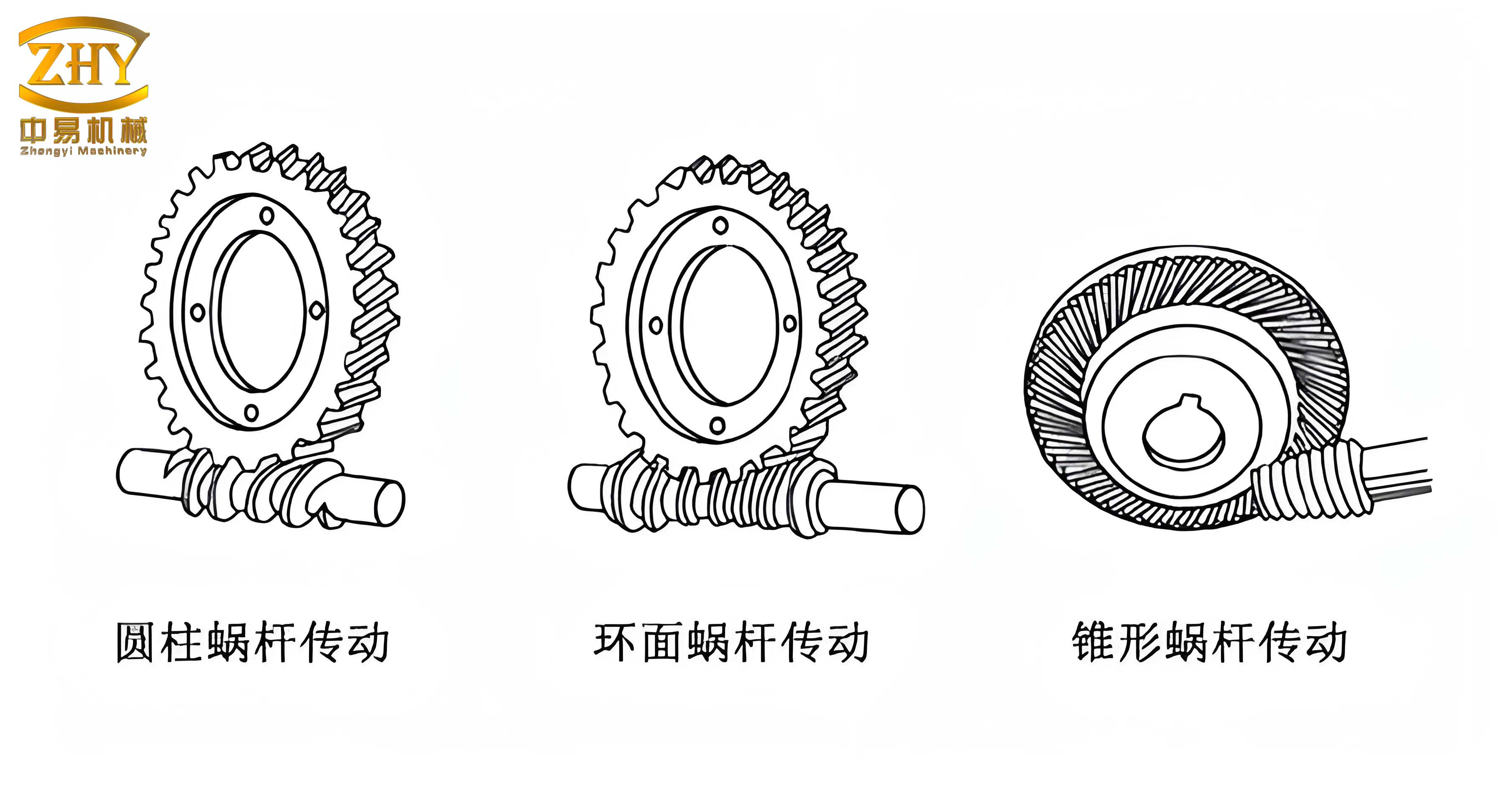
The fundamental superiority of the ZC1 screw gear lies in its unique manufacturing process and resulting geometry. Unlike cylindrical worms generated by a straight-edged tool, the ZC1 worm thread surface is generated as the envelope to a family of surfaces from a grinding wheel (or cutting tool) with a circular profile (torus shape) whose axis is tilted relative to the worm axis. Subsequently, the worm wheel tooth surface is generated as the envelope to this worm thread surface. This two-step enveloping process creates a localized “hour-glass” contact pattern where the worm, with a convex profile, meshes with the concave profile of the worm wheel. This conformation is highly favorable for establishing elastohydrodynamic lubrication (EHL) films, significantly reducing friction and wear, and increasing the contact area, thereby boosting load capacity. The study of the meshing zone—the region on the worm wheel face where contact can theoretically occur during a full mesh cycle—is therefore critical. Its size and shape are direct indicators of the potential load-bearing capacity and smoothness of motion transmission in these screw gears. A larger, well-centered meshing zone typically correlates with higher torque capacity and better durability.
Geometric Model and Mathematical Foundation
The mathematical modeling of ZC1 screw gears begins with defining a series of coordinate systems to describe the spatial relationships during the generation and meshing processes. The derivation follows the rigorous methodology of gear meshing theory.
Coordinate Systems:
- $S_u(O_u, x_u, y_u, z_u)$: Fixed to the grinding wheel/tool, with the $z_u$-axis coincident with the tool’s axis of rotation.
- $S_{u’}(O_{u’}, x_{u’}, y_{u’}, z_{u’})$: Fixed to the circular arc profile of the tool.
- $S_1(O_1, x_1, y_1, z_1)$: Fixed to the worm, with the $z_1$-axis coincident with the worm’s axis.
- $S(O, x, y, z)$: A fixed global coordinate system.
- $S_2(O_2, x_2, y_2, z_2)$: Fixed to the worm wheel.
The worm thread surface $\Sigma_1$ is the envelope of the tool surface. The family of tool surfaces in $S_1$ is represented by the vector function $\vec{r}_1(\theta, \psi)$, where $\theta$ is the parameter defining a point on the tool’s circular profile, and $\psi$ is the rotation angle parameter of the worm during generation. The meshing condition (equation of contact) is given by the scalar product of the relative velocity vector and the surface normal vector being zero: $\vec{n} \cdot \vec{v}^{(12)} = 0$. Solving this system yields the worm surface equations.
Worm Thread Surface ($\Sigma_1$):
The position vector of a point on the worm surface in coordinate system $S_1$ can be derived as:
$$
\vec{r}^{(1)}(\theta, \psi) = \begin{bmatrix}
x_1 \\
y_1 \\
z_1
\end{bmatrix} = \begin{bmatrix}
(\rho \sin\theta + d)(-\cos\beta\cos\psi + \sin\beta\sin\psi\cos\gamma_n) – (\rho\cos\theta – a)\sin\psi\sin\gamma_n + A_u\cos\psi \\
(\rho \sin\theta + d)(\cos\beta\sin\psi + \sin\beta\cos\psi\cos\gamma_n) – (\rho\cos\theta – a)\cos\psi\sin\gamma_n – A_u\sin\psi \\
(\rho \sin\theta + d)\sin\beta\sin\gamma_n + (\rho\cos\theta – a)\cos\gamma_n – p\psi
\end{bmatrix}
$$
where the parameter $\theta$ and the rotation angle $\psi$ are linked by the meshing equation for the generation process:
$$
\tan\theta = \frac{A_u – p\cot\gamma_n – d\cos\beta}{a\cos\beta + (A_u\cot\gamma_n + p)\sin\beta}
$$
Parameters:
- $\rho$: Radius of the circular profile arc of the tool.
- $a, d$: Coordinates defining the center of the circular profile arc in the tool coordinate system.
- $\gamma_n$: Crossed-axes angle between the worm and tool axes during grinding.
- $\beta$: Swivel angle of the tool profile.
- $A_u$: Center distance between the worm blank and the tool during grinding.
- $p$: Screw parameter of the worm ($p = \frac{m z_1}{2}$, where $m$ is the module, $z_1$ is the number of worm threads).
Analysis of the Meshing Zone and Undercutting Boundary
The meshing zone on the worm wheel face is bounded by the entry and exit paths of the tips of the worm and the worm wheel. This zone defines the total area of possible contact. Its calculation is essential for evaluating the performance potential of a given screw gear design.
1. Boundary Curve ‘a-a’ (Worm Tip Entry/Exit):
This curve is the locus of contact points when the tip of the worm thread ($r = r_{a1}$, the worm tip radius) is in mesh. Its parametric equations in the fixed plane (or in the worm wheel coordinate system $S_2$ after transformation) can be expressed as:
$$
\begin{aligned}
x &= r_{a1} \cos(\theta_e + \zeta + \phi_1) \\
y &= r_{a1} \sin(\theta_e + \zeta + \phi_1) \\
z &= \frac{r_{a1} \left[ r_{a1}\cos(\theta_e + \zeta + \phi_1) + A_0 – \frac{p}{i_{21}} \right] \cos \mu_e}{p \sin(\theta_e + \zeta + \phi_1 + \mu_e)}
\end{aligned}
$$
Here, $A_0$ is the working center distance of the worm gear pair, $i_{21}$ is the gear ratio ($z_1/z_2$), $\phi_1$ is the rotation angle of the worm, $\zeta$ is related to the worm’s helical motion, and $\mu_e$ is the pressure angle at the worm tip, calculated from the worm surface geometry and normal vector. The parameter $\theta_e$ corresponds to the specific $\theta$ value on the worm surface where the radial distance equals $r_{a1}$.
2. Boundary Curve ‘b-b’ (Worm Wheel Tip Entry/Exit):
This curve is the locus of contact points when the tip of the worm wheel tooth ($r = r_{a2}$, the worm wheel tip radius) is in mesh. Its equations are similar but evaluated at the worm wheel tip condition:
$$
\begin{aligned}
x &= r \cos(\theta + \zeta + \phi_1) \\
y &= r \sin(\theta + \zeta + \phi_1) \\
z &= \frac{r \left[ r\cos(\theta + \zeta + \phi_1) + A_0 – \frac{p}{i_{21}} \right] \cos \mu}{p \sin(\theta + \zeta + \phi_1 + \mu)}
\end{aligned}
$$
In this case, $r$ and the corresponding $\theta$, $\mu$ are determined by satisfying the condition that the contact point lies on the worm wheel tip circle in the meshing geometry.
3. Undercutting (Root Cutting) Boundary Curve:
Undercutting is a severe form of interference that weakens the tooth root of the worm wheel. It occurs at points on the generated worm wheel surface where the relative velocity of the generating worm is tangent to the contact line. Mathematically, this is defined by the so-called “limit function” $\Psi^{(12)}$ becoming zero along with the meshing equation:
$$
\begin{cases}
\vec{n} \cdot \vec{v}^{(12)} = 0 \\
\Psi^{(12)} = 0
\end{cases}
$$
Solving this system yields a set of equations that define the undercutting boundary curve on the worm wheel tooth surface. This curve represents the innermost limit of usable tooth area. A viable design must ensure this boundary lies outside the active meshing zone defined by curves ‘a-a’ and ‘b-b’. The equations for points on this boundary curve in the worm coordinate system $S_1$ are complex but can be numerically solved using the condition:
$$
r^{(1)} \left[ r^{(1)} \cos(\theta + \phi_1 + \zeta) + A_0 – \frac{p}{i_{21}} \right] \cos \mu = p^2 \zeta \sin \tau
$$
where $\tau$ is an auxiliary angle derived from the kinematics. The corresponding coordinates on the worm wheel ($\vec{r}^{(2)}$ in $S_2$) are obtained through the standard coordinate transformation from $S_1$ to $S_2$.
Parametric Study and Influence on Meshing Characteristics
Using numerical software to solve the systems of equations described above, the meshing zone and undercutting boundary can be plotted for any given set of parameters. This allows for a systematic study of how key design variables influence the performance of ZC1 screw gears. For this analysis, a base design is considered: Center distance $A_0 = 180$ mm, module $m = 8.7$ mm, number of worm threads $z_1 = 1$, diameter quotient $q = 10$. One parameter is varied at a time while others are held constant to isolate its effect.
1. Influence of Pressure Angle ($\alpha$)
The pressure angle $\alpha$ (often corresponding to the nominal pressure angle of the tool profile) is a fundamental parameter influencing tooth strength and the direction of the contact force. The analysis was performed for $\alpha = 21^\circ, 22^\circ, 23^\circ,$ and $24^\circ$, with $\rho = 48$ mm and $x = 0.5$ held constant.
| Pressure Angle $\alpha$ | Observed Effect on Meshing Zone Area | Observed Effect on Undercutting Region | Qualitative Trend |
|---|---|---|---|
| $21^\circ$ | Largest area among the set | Undercutting region is most prominent, encroaching significantly into the potential contact area. | Favorable for contact area, unfavorable for avoiding interference. |
| $22^\circ$ | Slightly reduced compared to $21^\circ$ | Undercutting region is reduced but still present. | Trade-off between area and interference begins to improve. |
| $23^\circ$ | Moderate, well-defined area | Undercutting boundary is minimized or pushed outside the practical meshing zone. | Often considered an optimal balance. Provides a good, safe contact area. |
| $24^\circ$ | Smallest area among the set | Undercutting is effectively eliminated. | Maximizes resistance to undercutting but at the cost of reduced contact area. |
Conclusion: Increasing $\alpha$ consistently reduces the risk and extent of undercutting in ZC1 screw gears. However, this benefit comes with a gradual reduction in the total theoretical meshing zone area. The value of $23^\circ$ is frequently cited in design handbooks as a standard compromise, offering a sufficiently large contact area while robustly avoiding interference—a key consideration for the long-term reliability of these screw gears.
2. Influence of Profile Arc Radius ($\rho$)
The profile arc radius $\rho$ defines the curvature of the generating tool and thus the concavity/convexity of the mating surfaces. The analysis was performed for $\rho = 45, 48, 50,$ and $52$ mm, with $\alpha = 23^\circ$ and $x = 0.5$.
| Arc Radius $\rho$ (mm) | Observed Effect on Meshing Zone Area | Observed Effect on Undercutting Region | Qualitative Trend |
|---|---|---|---|
| 45 | Relatively larger area | Undercutting region is noticeable. | Tighter curvature, more sensitive to undercutting. |
| 48 | Slightly reduced area | Undercutting boundary is receded. | Improved contact conformity over smaller $\rho$. |
| 50 | Moderate area | Undercutting is minimal. | Commonly used value providing good balance. |
| 52 | Smallest area in this set | Undercutting is virtually absent. | Flatter curvature maximizes interference avoidance but minimizes theoretical contact patch size. |
Conclusion: Similar to the pressure angle, increasing $\rho$ (making the tool profile flatter) reduces the undercutting tendency but also leads to a modest decrease in the size of the meshing zone. The selection of $\rho$ is therefore a critical step in balancing the contact stress (smaller $\rho$ gives more conformal contact but higher stress concentration) with the geometric constraints of undercutting. For the given module, a $\rho$ value around 48-50 mm strikes a practical balance for these screw gears.
3. Influence of Profile Shift Coefficient ($x$)
The profile shift coefficient $x$ is a powerful tool in the design of screw gears. A positive shift moves the worm wheel tooth thicker at the root and thinner at the tip, altering the meshing geometry significantly. The analysis was performed for $x = 0.4, 0.5, 0.75,$ and $1.0$, with $\alpha = 23^\circ$ and $\rho = 48$ mm.
| Shift Coefficient $x$ | Observed Effect on Meshing Zone Area | Observed Effect on Undercutting Region | Qualitative Trend & Implications |
|---|---|---|---|
| 0.4 | Largest theoretical meshing area. | Substantial undercutting region, severely cutting into the usable area. | The effective, safe contact area is significantly less than the theoretical area. |
| 0.5 | Reduced theoretical area. | Undercutting region is reduced, freeing up more of the theoretical area for safe contact. | The effective contact area may be comparable to or even greater than at $x=0.4$. |
| 0.75 | Significantly smaller theoretical area. | Undercutting is nearly or completely eliminated. | Almost the entire theoretical meshing zone is usable, and contact lines are favorably oriented for oil film formation. |
| 1.0 | Smallest theoretical area. | No undercutting. | Maximizes tooth root strength and provides excellent lubrication conditions, albeit with a compact contact patch. |
Conclusion: The profile shift coefficient $x$ has the most dramatic and complex influence on the meshing characteristics of ZC1 screw gears. While a larger $x$ unequivocally shrinks the theoretical meshing zone, it more importantly and powerfully suppresses undercutting. This means the effective, safe contact area does not simply decrease with $x$; it often increases up to an optimum point as the undercutting region recedes. Furthermore, a larger positive shift improves the shape and orientation of the instantaneous contact lines, promoting the formation of a hydrodynamic lubricant film—a crucial factor for the high efficiency of these screw gears. Therefore, contrary to intuition, selecting a larger positive profile shift coefficient is generally advantageous for optimizing the overall performance and durability of ZC1 worm gear sets.
Optimization Strategy and Design Synthesis for ZC1 Screw Gears
The parametric analysis reveals that designing high-performance ZC1 screw gears is a multi-objective optimization task. The goal is to maximize the effective, undercutting-free meshing area while ensuring favorable conditions for lubrication and adequate tooth strength. The following synthesis strategy emerges:
- Primary Lever: Profile Shift ($x$): This is the most effective parameter to control undercutting. A positive shift should be applied, typically in the range of $x = 0.5$ to $1.0$ or higher, depending on the gear ratio and center distance. This choice directly enhances tooth root strength and improves the lubrication regime by modifying the contact line geometry.
- Secondary Adjustment: Pressure Angle ($\alpha$): With a sufficient positive shift mitigating undercutting, the pressure angle can be selected to fine-tune the contact area and bending strength. A standard value of $\alpha = 23^\circ$ is a robust starting point. Slight reductions (towards $21^\circ$) may be considered if analysis confirms no undercutting and a larger contact area is paramount, though this may slightly increase radial loads.
- Tertiary Tuning: Profile Arc Radius ($\rho$): This parameter is often linked to the module ($m$). A common empirical relation is $\rho \approx (5.5 \text{ to } 6.0)m$. Within this range, the specific value can be adjusted to optimize contact stress and conjugate action. A value from the upper end of this range ($\rho \approx 6.0m$) supports the trend of reducing undercutting risk.
The optimal design is found at the intersection where the undercutting boundary lies just outside the practical working zone defined by the worm and wheel tip boundaries. Modern design leverages numerical simulation software to solve the complete meshing equations, plot the boundaries, and iteratively adjust parameters until an optimal configuration is found. This computational approach allows designers to visualize the trade-offs and achieve a tailored solution for specific applications, whether prioritizing maximum load capacity, highest efficiency, or minimal size in screw gears.
Conclusion and Future Perspectives
The torus envelope (ZC1) worm gear represents a sophisticated evolution in screw gear technology. Its superior performance stems from the favorable concave-convex contact condition engineered through a double-enveloping process. This analysis has systematically deconstructed the relationship between key design parameters—the pressure angle $\alpha$, the profile arc radius $\rho$, and the profile shift coefficient $x$—and the fundamental meshing characteristics of zone size and undercutting. The findings underscore that a simplistic maximization of the theoretical meshing area is not the path to an optimal design. Instead, a holistic approach that uses a significant positive profile shift to eradicate undercutting and shape the contact lines for effective lubrication, followed by fine-tuning of the pressure angle and arc radius, yields the most robust and efficient screw gears.
Future work in this domain will likely focus on the integration of these geometric optimizations with advanced material science, surface engineering (coatings, textures), and tribological modeling. Furthermore, the application of topological modification (deliberate flank corrections) to the ZC1 surfaces to optimize load distribution under actual operating deflections and thermal expansions is a promising avenue for pushing the performance boundaries of these already exceptional screw gears even further. The ZC1 design, with its strong theoretical foundation and demonstrable practical benefits, will undoubtedly remain a cornerstone of high-performance power transmission in demanding applications for the foreseeable future.
