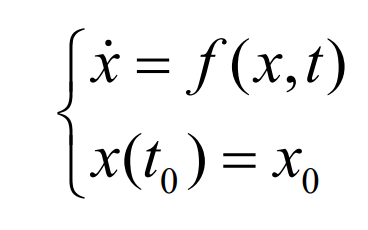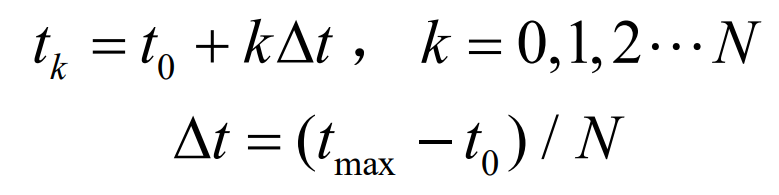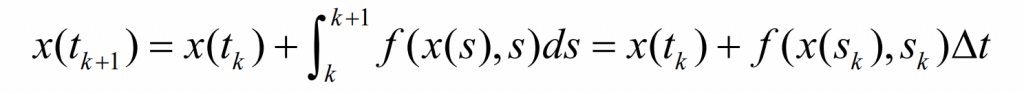There are many methods to solve the dynamic response characteristics of spiral bevel gear transmission, such as analytical method, numerical method and phase space method. However, due to the complex and nonlinear characteristics of multi degree of freedom differential equations of spiral bevel gear transmission system, the application of analytical method and imaginary space method can not meet the requirements. With the rapid development of computer science, numerical methods for complex nonlinear systems have been widely used. Numerical method divides the equation of motion into smaller time intervals for integration, mainly including gill method with fixed step size and variable step size, Runge Kutta method with fixed step size and variable step size, Euler method, etc. Among them, Runge Kutta method is the most widely used.
Using Matlab toolbox, the Runge Kutta method with variable step size is used to solve the differential equation of system vibration. The basic idea is as follows:
For differential equations and their known initial value conditions:
Take a sufficiently large positive integer n and discretize the time period [T0, Tmax] into:
In each short time interval, the equation is integrated. According to the integral mean value theorem:
By calculating the above approximate value of k s, we can obtain the approximate value k s of X (T) discrete on [T0, Tmax]. The Runge Kutta method is solved by using this principle. Its core idea is to use the linear combination of values at a certain point to construct the formula, expand it through the Taylor formula, and compare it with the Taylor formula of the solution of the initial value problem, so as to make as many terms as possible the same, so as to obtain the parameters, so as to ensure the high-precision solution.