After the detailed grid data is predicted, if the output torque of P20 row is expressed as 1, then the output torque of P10 row is tout. When the engaging forces of two rows are in the same phase, the maximum value of the engaging forces of a single row is calculated by the formula
Where ∑ fhp10 is ∑ FH in P10 row, which can be obtained from the predicted value ∑ FB in P10 row, and ∑ fhp20 corresponds to it.
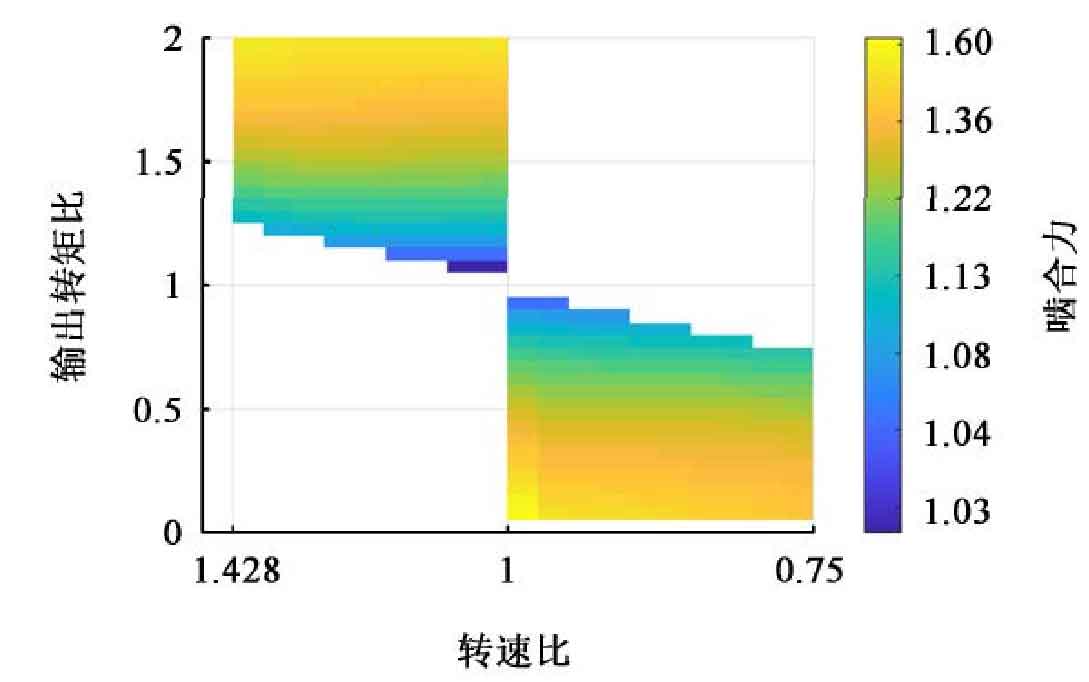
As shown in the figure, it is the maximum of single row engagement force. In Fig. (a) and (b), the change of the maximum value of the two rows of meshing force is relatively close. In the overall trend, the larger the deviation of the meshing force from 1, the larger the maximum value of the meshing force. Under the same output torque ratio, the influence of speed ratio is small, and the maximum meshing force occurs when the speed ratio is 0.967 and the output torque ratio is 0.1. The influence of speed ratio is small, which is related to the narrow range of speed ratio.
As shown in the figure, the physical meaning of the relationship between the speed ratio and the output torque ratio can be expressed as follows: when the speed ratio is greater than 1, row P10 turns to the high-speed side; When the speed ratio is less than 1, P10 turns to the low speed side and P20 turns to the high speed side; The farther the speed ratio deviates from 1, the greater the speed difference between the two sides, and the smaller the steering radius.
Combined with the distribution of the meshing force, it can be seen that the output torque ratio has a greater influence on the meshing force, while the steering radius has a smaller influence on the meshing force. When the vehicle turns, the greater the resistance on both sides, the greater the meshing force of parallel planetary gears.