The integral time range of solving differential equations is 300tm. In order to solve this problem, it is necessary to reduce the order of the second order vibration differential equation step by step. The equation can be expressed as: x2 = f (T, X (1), X (2)).
Influence of rotational speed on nonlinear vibration characteristics of gear transmission system
Gear transmission is gradually developing towards high speed and heavy load. Therefore, it is necessary to carry out systematic research on the influence of speed on the vibration characteristics of the system, and set the dimensionless frequency of the transmission system in the range of Ω = 0.001 ~ 1.5. When Ω is less than 0.2, the system presents a single period anharmonic response. At this time, the time history of the system displacement is a single period curve, and the spectrum is distributed on the discrete points of M Ω. With the increase of dimensionless frequency, the system will change from period doubling bifurcation to chaotic motion. With the increase of frequency, the response state of the system changes irregularly and the motion state is more complex and changeable. There are many periodic windows in the chaotic region, and the width of the window is gradually changing. With the frequency increasing again, the dynamic load coefficient of gear pair will increase, and the system will show unilateral and bilateral impact in the state of no impact. When the dimensionless frequency increases to near 1, the dynamic load coefficient reaches the maximum, and the impact is the most serious.
Effect of viscous friction coefficient on the performance of transmission system
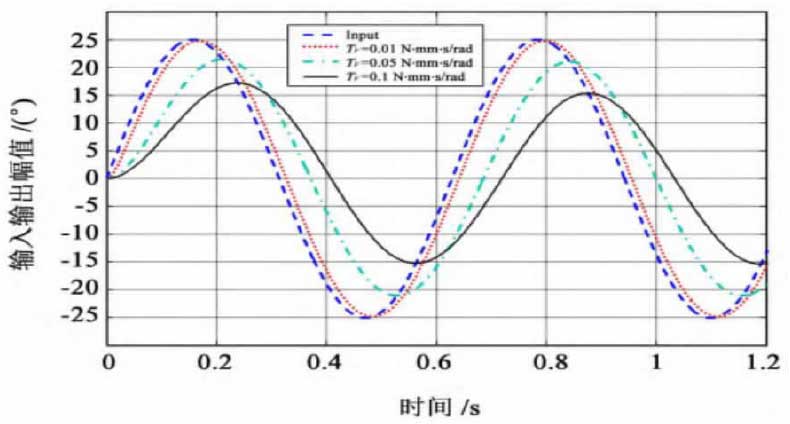
The response curves of different viscous friction coefficients can be obtained by simulation analysis, as shown in Fig. 1, while the step response curves of the system are shown in Fig. 2.
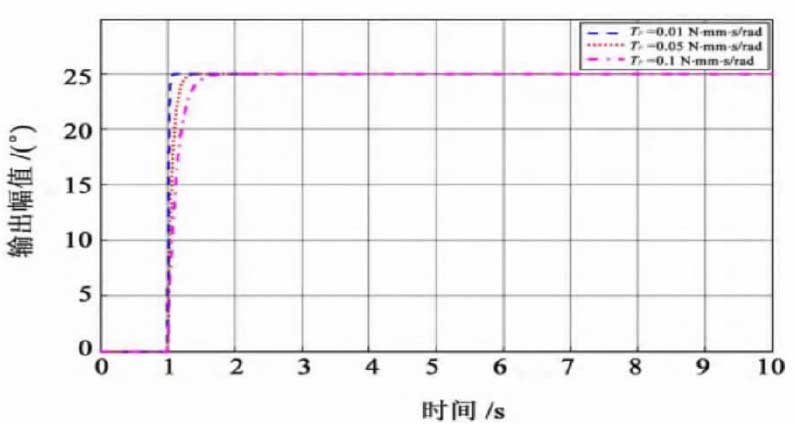
Through figure 1 and Figure 2, the influence of viscous friction coefficient on the dynamic performance of transmission system can be obtained. With the increase of viscous friction factor, the phase difference of transmission system is also gradually expanding. The main reason for this problem is: with the increase of viscous friction coefficient, the friction torque in the transmission system will also rise, which means that with the rising of damping parameter in friction dynamic equation, these reactions will appear. In addition, it will lead to the gradual decline of mechanical efficiency in multi-stage gear transmission system. Therefore, in the process of designing the transmission system, it is necessary to consider a certain speed and efficiency of the transmission system. Under this premise, the viscous friction coefficient of the system can be effectively reduced.
Influence of backlash between teeth on performance of multistage gear transmission system
If the backlash is used in the simulation model, the response curve is shown in Fig. 3. After using different backlash, the step response curve of the system is shown in Fig. 3.
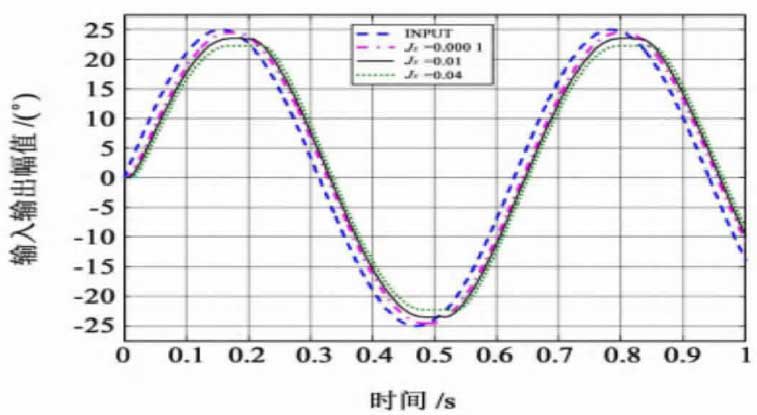
Based on Figure 3 The influence of the transmission clearance on the dynamic performance of the system is mainly reflected in: when there is a gap in the transmission system, the stability and rapidity of the response will decline. At the same time, because of the gap, although the transmission system can achieve the best stable state, the transmission system will also have a certain amplitude of vibration, and for the stability of the whole work Sex has a serious impact. Therefore, in the process of design and manufacturing of multi-stage gear transmission system, it is necessary to take the system motion lubrication as the premise, and at the same time, to eliminate the assembly clearance and error in the transmission system as far as possible, so as to ensure the design function of the transmission system.
