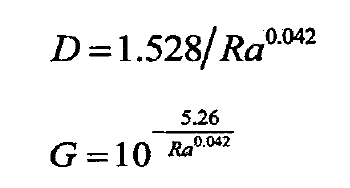According to the measured data and theoretical calculation analysis of surface micro topography roughness of machining parts, the approximate relationship between roughness Ra and fractal dimension D, roughness amplitude G is obtained as a formula, showing a power exponential coordination relationship.
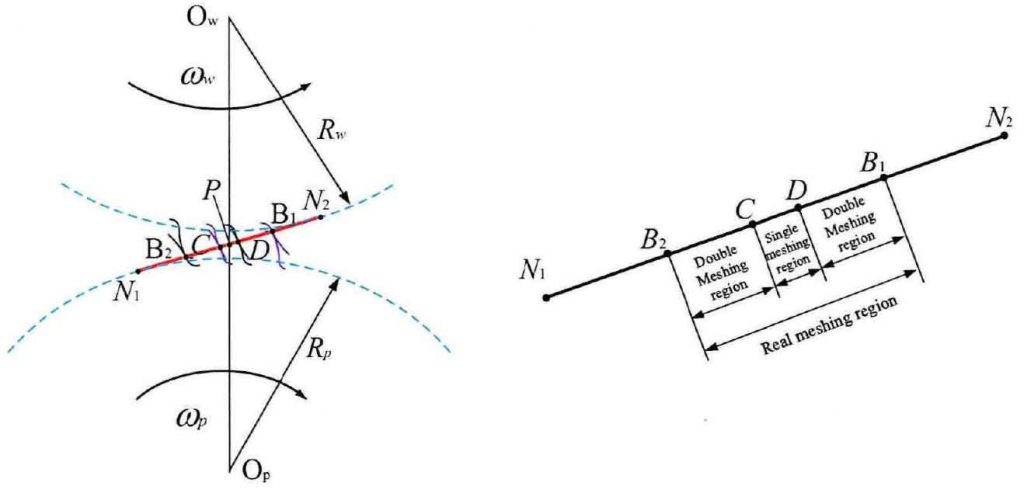
In view of the tooth meshing process of a pair of spur gears with coincidence degree in the range of L <ε< 2 as shown in Fig. 1, the single and double alternate meshing occurs along the meshing line tooth surface. Because the single pair of teeth in the single meshing area bear the load completely and the contact effect is obvious, the CP section of the single pair meshing area is selected as the research object.
According to the drawing method of bobillier’s law and the basic parameters of involute gear profile, the relationship between the curvature radius and the meshing angle of any meshing point in CP section of single tooth pair meshing area is derived, as shown in the formula. According to the Hertz elastic contact theory of two cylinders, the relationship between half width of meshing contact, nominal contact area and meshing angle is derived. See the formula.
Where;
M-modulus;
ZP, ZW – number of teeth of driving and driven gears;
A – pressure angle;
APM, AWM contact angle of driving and driven gears;
P0 – power;
N – rotational speed;
RPM – contact radius of driving wheel;
F – load;
B – tooth width;
B-contact half width;
ρ PM, ρ WM the radius of curvature of the contact point of the driving and driven gears.
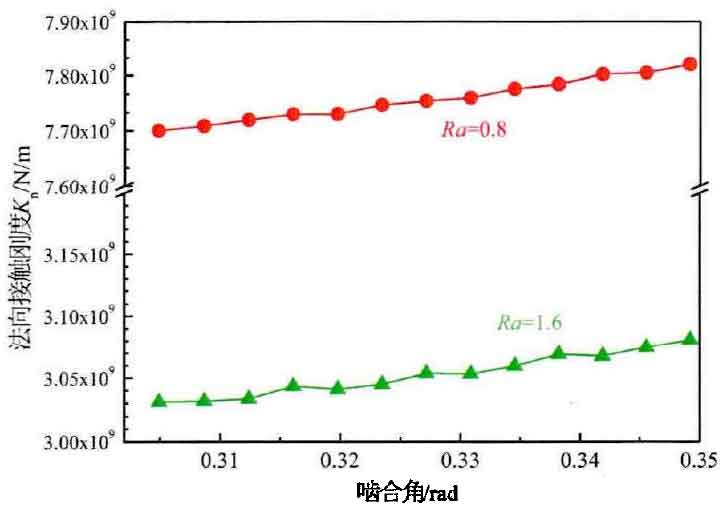
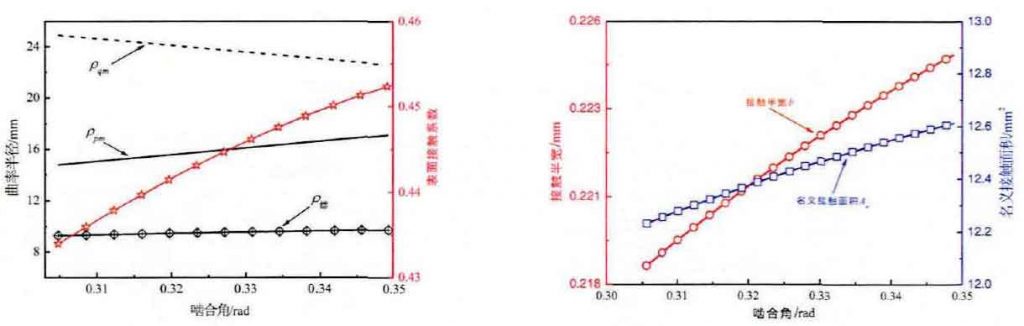
By substituting the basic parameters of involute spur gear pair into the formula, the relationship diagram of relevant derived parameters varying with meshing angle can be obtained, as shown in Figure 2. Figure 2 (a) shows that the comprehensive curvature radius and surface contact coefficient increase slightly from the meshing point C to the node, and Figure 2 (b) shows that the contact half width and nominal contact area also increase.
Four kinds of different roughness are selected to calculate the normal contact stiffness of the tooth surface. The existing gear processing technology (hobbing / grinding, finishing, etc.) and the precision roughness value of the tooth surface applied in engineering are simulated. The fractal parameters of the relevant fractal model are obtained by substituting the four kinds of simulation values into the formula. The data in the table show that with the increase of roughness, the fractal dimension decreases (the rougher the fractal is), and the roughness amplitude increases (the lower the surface finish is). The mutual variation trend is consistent with the real surface morphology.
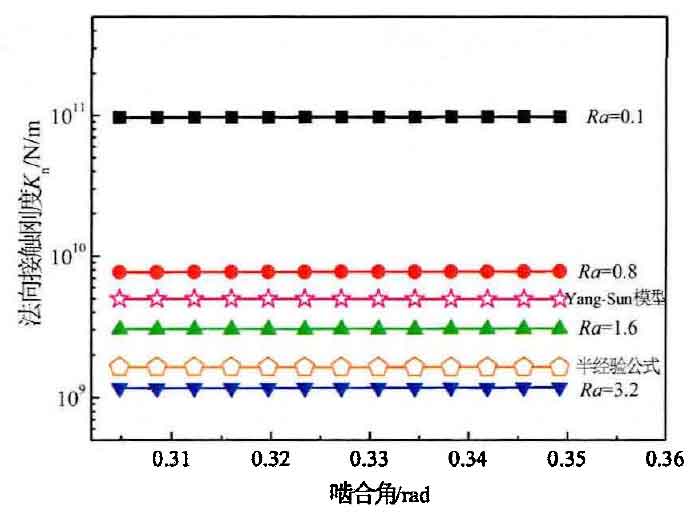
The design parameters are substituted into the fractal model of the normal contact stiffness of the tooth surface to carry out simulation analysis and calculation. Figure 3 shows that the normal contact stiffness along the CP section increases slightly under the same processing technology, which is different from the Yang sun model which is considered as linear. Figure 4 shows that the normal contact stiffness decreases with the roughness under different processing precision (the higher the surface topography precision is) )The normal contact stiffness of RA = 0.1 is significantly higher than other roughness values, which has the same effect as improving the surface accuracy to enhance the contact fatigue strength of gears. Compared with the Yang sun model and the semi empirical formula proposed in NASA technical report, the order of normal contact stiffness of the proposed model and the two models under the action of common machining is 10000000000. According to the stiffness curve distribution, the Yang sun model is between RA = 0.8-1.6, because the model is independent of load and deformation, that is, geometric parameters The results show that the contact stiffness is a constant value, which is contrary to the actual action, and the semi empirical formula is between RA = 1.6-3.2.
The two models do not take the contact surface morphology into account, so there will be graphical differences. It can be seen from the results that the normal contact stiffness of the tooth surface has different response characteristics under different machining processes. It can be seen that for the service engineering of high quality, high parameter and high performance gears, in addition to the macro size of the gear, it is also necessary to consider the micro morphology characteristics of the lower surface under different machining processes to qualitatively and quantitatively analyze the contact characteristics, while the Yang sun model and the semi classical model are the best It can be used to predict the initial stiffness of the new gear.