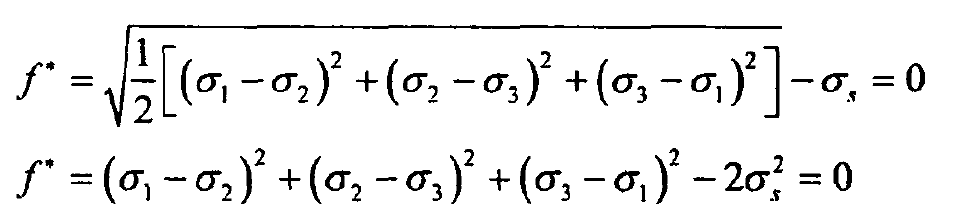Von Mises proposed for material conditions under complex stress:

The shape change energy density is:

Therefore, Mises yield condition is:

Because the above conditions are applicable to various stress conditions, for unidirectional tensile yield, that is, σ 1= σ 2， σ 2= σ When 3 = 0, substitute in:

Existing:

Then replace it back to the original formula to obtain Mises yield condition:

Obviously, in the principal stress space, the Mises yield surface can be simply and directly expressed as the side feature of the cylinder. And in σ 1- σ 2 plane (with σ 3 = 0), then:

This formula is an elliptic equation, that is, the yield curve determined by this formula is an elliptic curve. The Mises yield function is:

In plane problems, the principal stress formula:

The stress formula of open crack is as follows:

The substitution formulas are:

For plane stresses similar to thin and thick plate surfaces, there are σ 3 = 0. Substitute the formula into the solution to obtain:

This formula is the boundary equation of the yield region at the top of mode I crack (in the case of plane stress), which is drawn as a curve, as shown in Figure 1 (solid line). On the x-axis（ θ＝ The R value of 0) is:

For plane strain (center of thick plate):

Replace the above principal stresses into the formula, then:

In Figure 2, as shown by the dotted line (Poisson’s ratio μ＝ ０．３）。 On the x-axis（ θ＝ The R * value of 0) is

Tresca believes that the condition of material yield phenomenon can be expressed as: the maximum shear stress in the stress reaches the unidirectional tensile yield shear stress under the test of the material τ s. When using this criterion, τ s＝ σ S / 2, the shape and basic conclusion of the yield zone are basically consistent with the Mises criterion.