The vibration acceleration in all directions of the helical gear is synthesized into the relative vibration acceleration a in the direction of the end meshing line of the helical gear, and it is taken as the main index of the system vibration. Its expression is as follows:
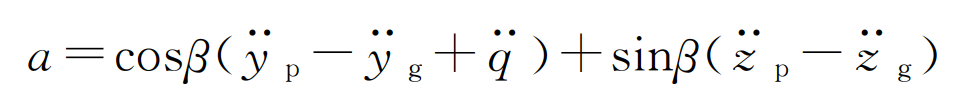
The obtained time-varying meshing stiffness and meshing impact force are substituted into the dynamic model, the obtained vibration accelerations in all directions are solved and synthesized according to the formula, and then the root mean square value of the relative vibration acceleration at each speed is obtained in turn. According to the above steps, the vibration response of the system under 80N · m, 100N · m and 120N · m3 input torques is obtained.
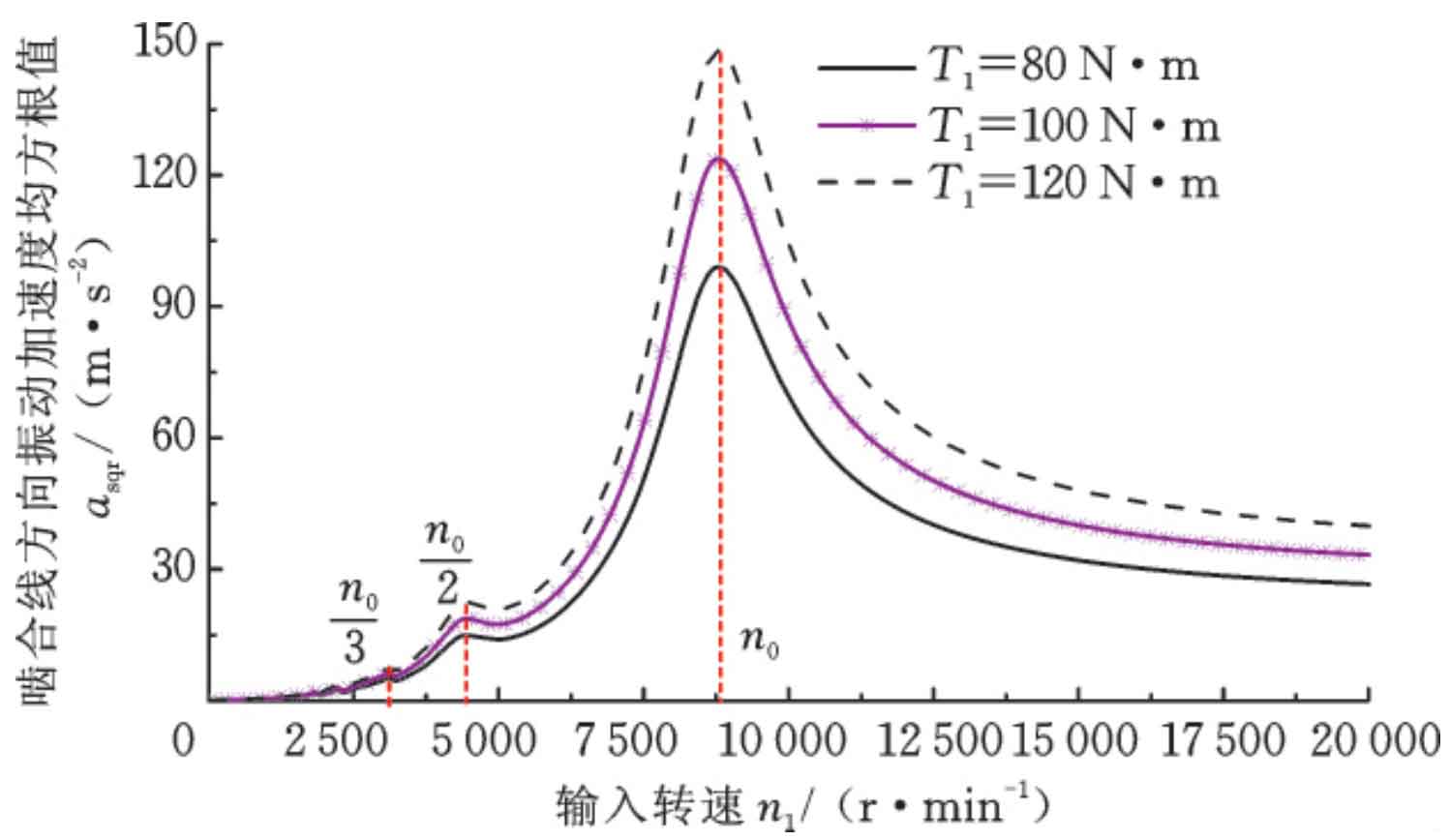
Fig. 1 vibration speed diagram of the system under three different loads when the time-varying meshing stiffness is excited alone. It can be seen that there is obvious superharmonic resonance at N0 / 3, N0 / 2 and N0 (N0 is the resonant speed); With the increase of load, the relative vibration acceleration increases; The root mean square value of acceleration outside the resonance peak does not change significantly with the speed, but decreases slightly in the over resonance region. That is, under this excitation, when it is far away from the resonant speed, the influence of speed increase on the vibration characteristics of the system is not significant.
This phenomenon is because the time-varying meshing stiffness is a kind of parametric excitation, and its mean value and amplitude are independent of speed. The vibration of the system under parametric excitation is caused by the periodic changes of internal parameters (meshing stiffness) of the system. After the speed increases to the resonance region, the frequency of parameter excitation gradually moves away from the resonance frequency, and the influence of parameter changes on the system also decreases. Therefore, in the over resonance region, the vibration of the system under the excitation of time-varying meshing stiffness does not increase with the speed.
Figure 2 shows the vibration speed diagram under three different loads when the meshing impact is excited alone. It can be seen that the relative vibration acceleration in the meshing line direction of the gear end face increases with the increase of the load; There are obvious superharmonic resonance at N0 / 4, N0 / 3, N0 / 2 and N0; The root mean square value of vibration acceleration outside the formant increases significantly with the increase of rotating speed; Far away from the resonant speed, the increase of speed has a significant impact on the vibration of the system. This is because the meshing impact force increases with the increase of rotating speed, and the growth trend is approximately linear. This is consistent with the conclusion in the helical gear manual that the dynamic load coefficient kV increases with the increase of the helical gear pitch speed.
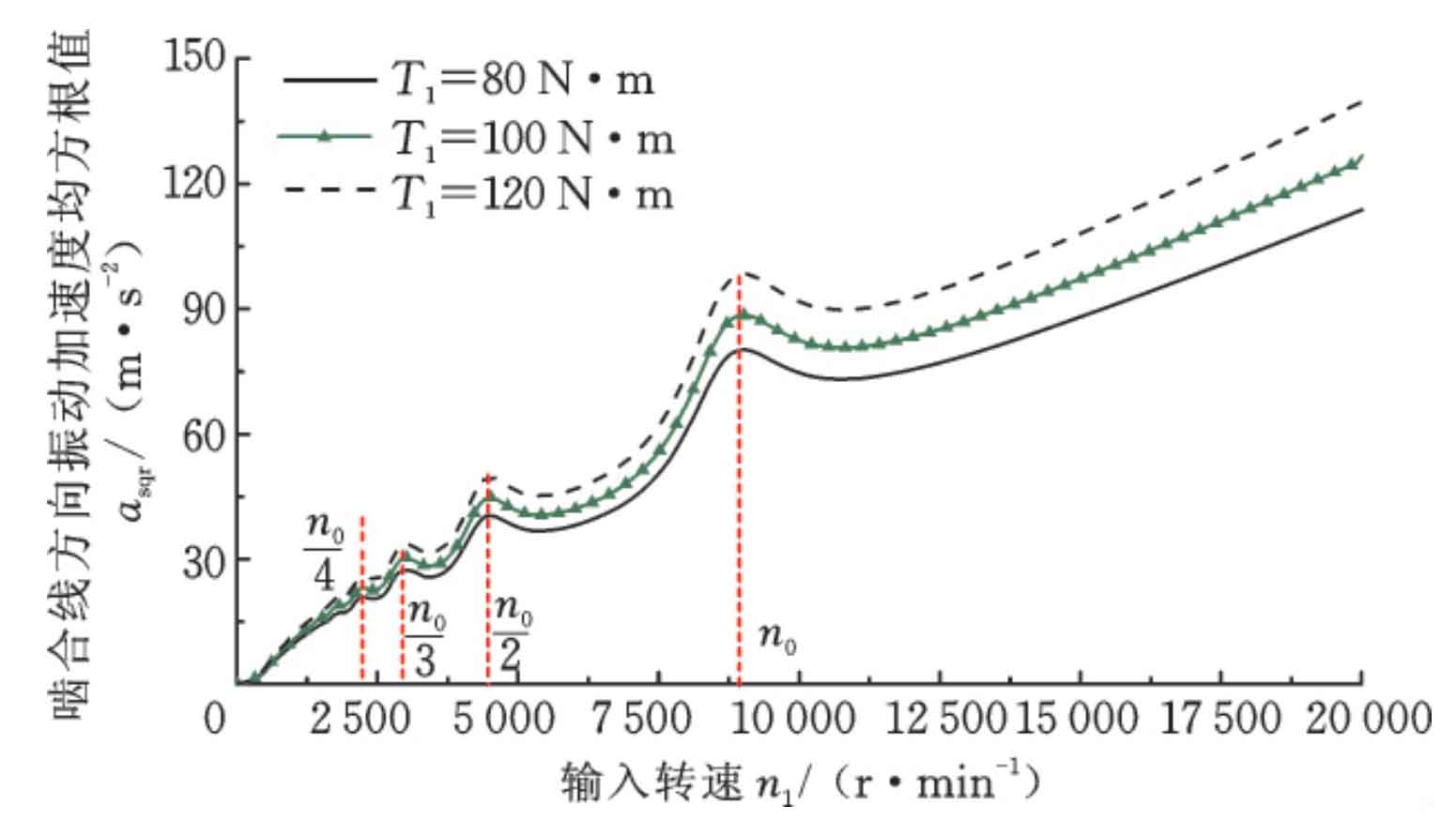
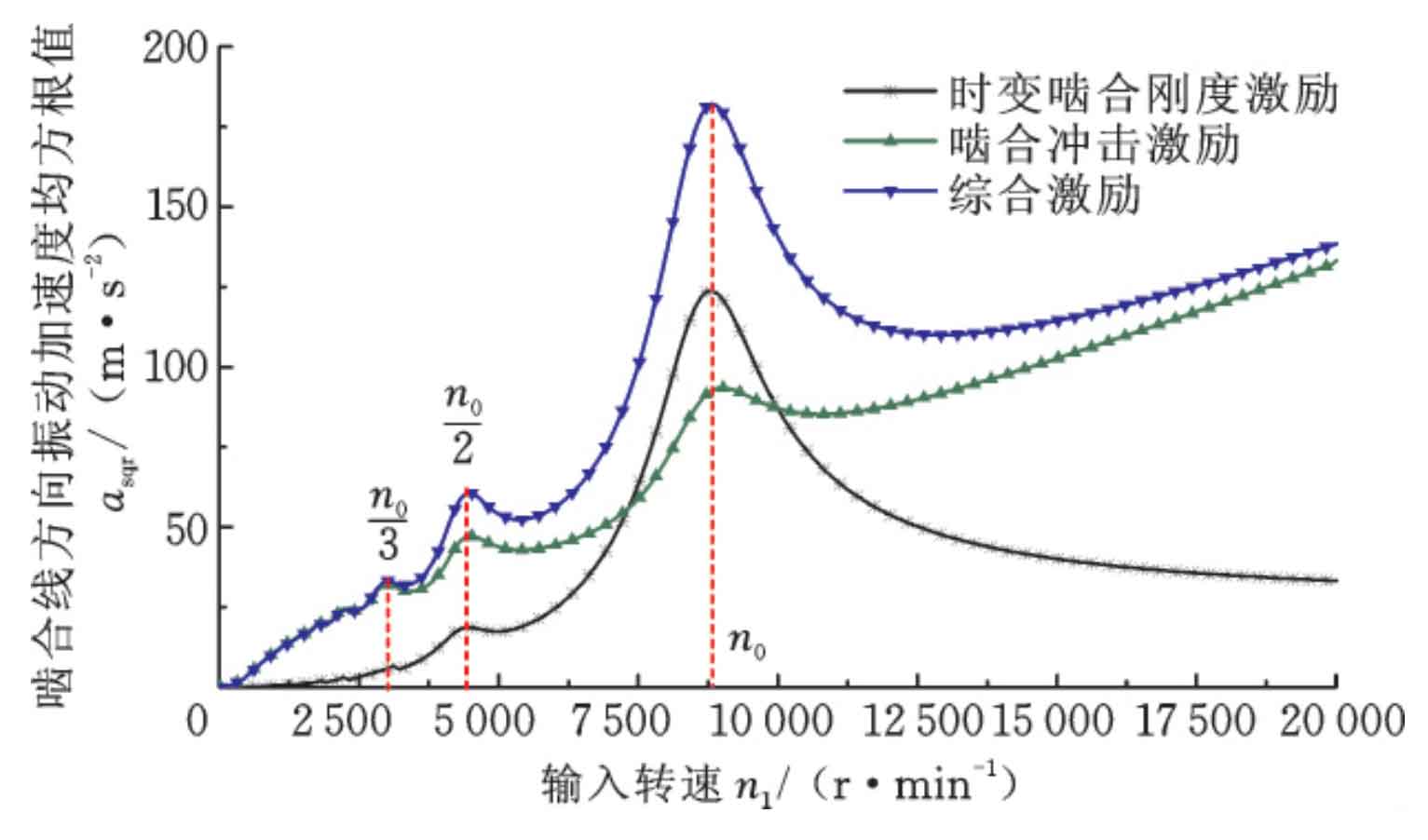
Fig. 3 vibration speed diagram under three different loads under the combined excitation of time-varying meshing stiffness and meshing impact. It can be seen that the relative vibration acceleration in the meshing line direction of helical gear end face increases with the increase of load; There are obvious superharmonic resonance at N0 / 3, N0 / 2 and N0; The root mean square value of vibration acceleration outside the resonance peak increases significantly with the increase of rotating speed, but its increasing trend is slower than that under the excitation of meshing impact alone. This is because in the resonance region, the vibration of the system under the excitation of time-varying meshing stiffness decreases slightly with the increase of rotating speed.
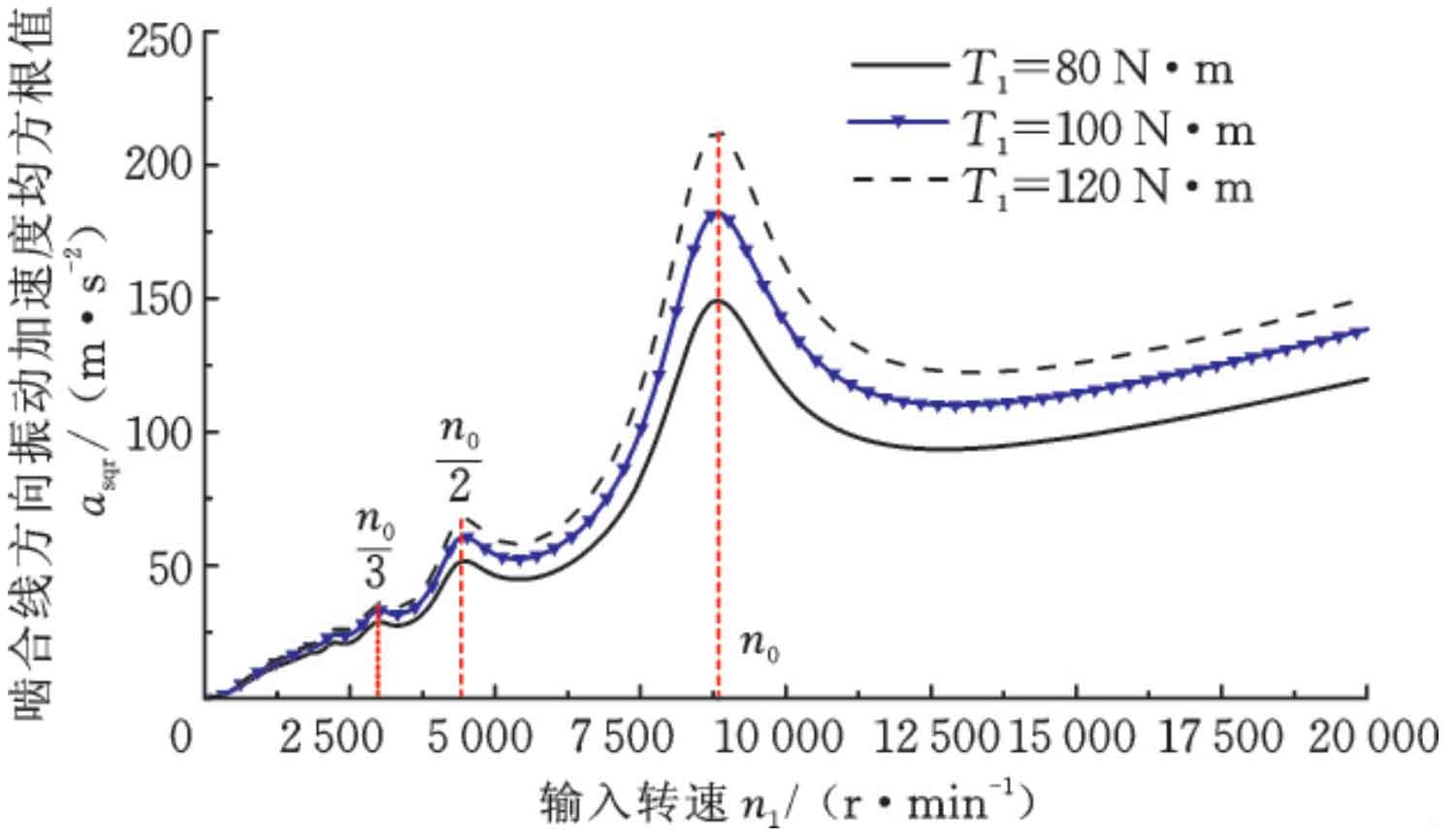
When the input torque is 100N · m, the vibration speed diagram of the system under three different excitations is compared, and the results are shown in Figure 4. It can be seen that the vibration of the system under the excitation of meshing impact alone is greater than that under the excitation of time-varying meshing stiffness; This is due to the large meshing stiffness of the pair of helical gears, so that the vibration response of the system under stiffness excitation is not large. When the speed is constant, the impact force is large when the meshing stiffness is large, so the vibration generated by meshing impact excitation is large at low speed; After passing the resonance zone, the system vibration under meshing impact and comprehensive excitation tends to be consistent with the increase of speed, indicating that meshing impact becomes the main excitation at high speed.
In order to study the time-domain and frequency-domain characteristics of helical gears under meshing impact excitation, the case under separate excitation of meshing impact at different speeds is analyzed, and the results are shown in Fig. 5 and Fig. 6.
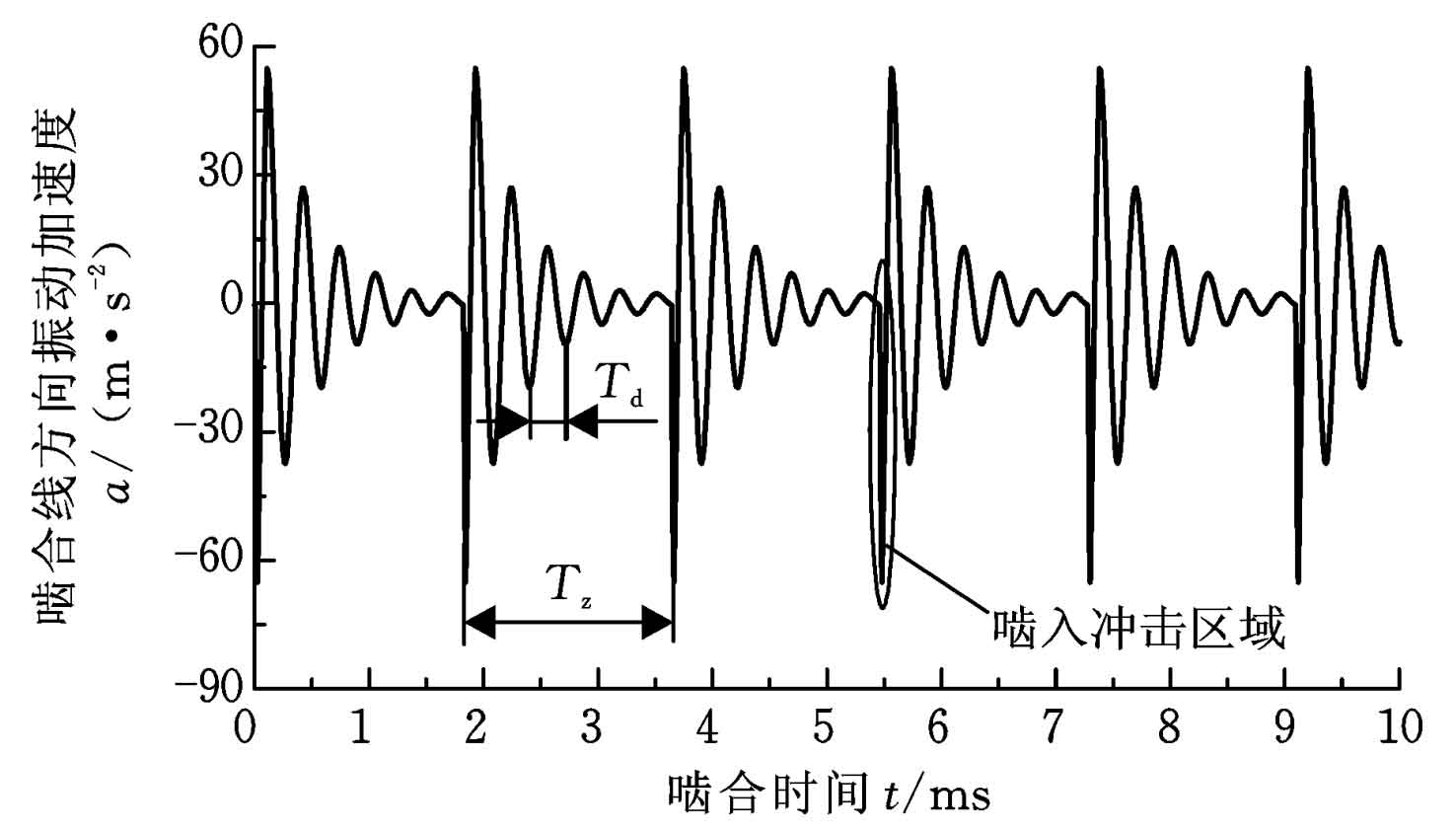
In Figure 5, the meshing impact zone is mainly characterized by a sudden change in the negative direction of vibration acceleration. This is because when the meshing impact occurs, the speed of the driven wheel will suddenly change. Combined with the formula, the relative vibration acceleration in the meshing line direction of the helical gear end face will suddenly decrease. In the figure, the vibration acceleration of the system gradually attenuates with TD as the cycle, and 1 / TD is the natural frequency of the system. When the speed increases, the meshing period TZ gradually decreases. When the meshing period TZ is the same as the vibration acceleration attenuation period TD, the system will resonate, such as the time domain diagram of 8900r / min under the meshing impact excitation (Fig. 6), in which 8900r / min is the resonant speed of the system.
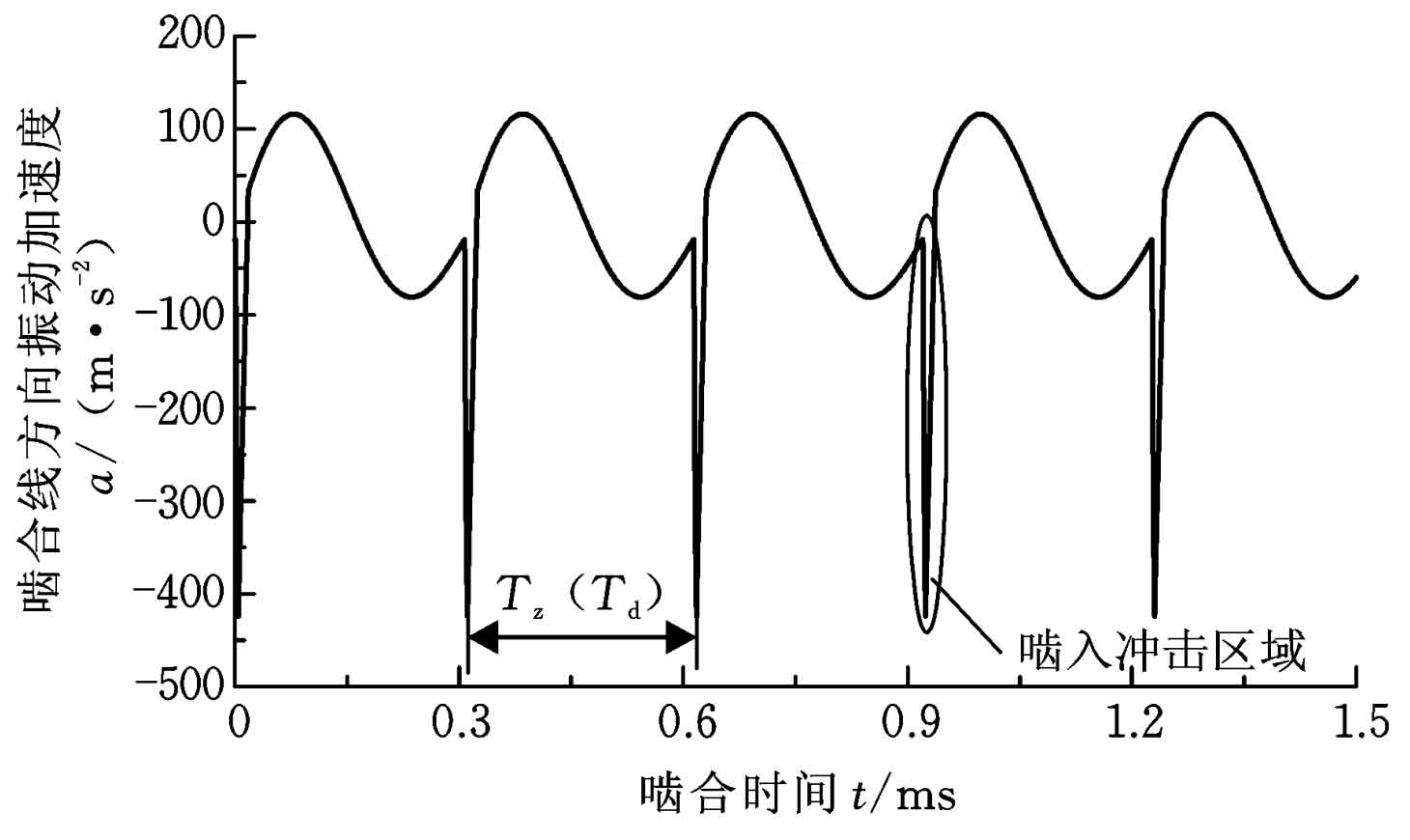
It is obvious from Figure 6 that after the previous impact, about one cycle TD will enter the next impact, which is consistent with the above analysis conclusion.
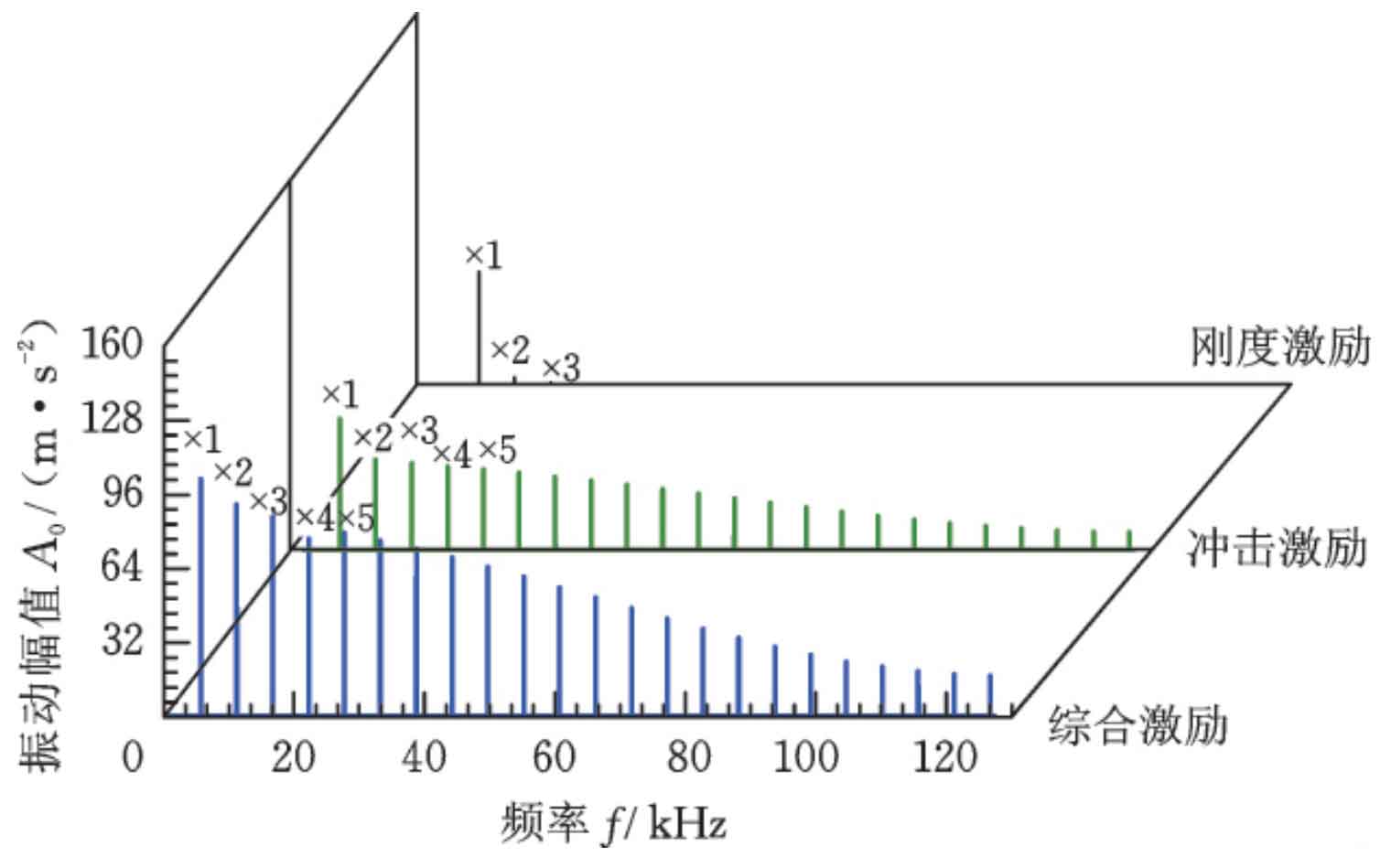
Figure 7 shows the frequency domain diagram under three different excitation conditions at 12000r / min. it can be seen that the amplitude is the largest at one time of tooth frequency, because one time of tooth frequency is closest to the resonance frequency; Under the excitation of time-varying meshing stiffness, the 3-fold tooth frequency decays almost to zero, while when there is an impact excitation component, the 20 fold tooth frequency still has a certain frequency, which decays slowly. This is because the meshing impact waveform is similar to the pulse, and the narrower the pulse, the more high-frequency components, so the existence of impact excitation makes the vibration response of the system more complex. This situation is more prominent in the high-speed state of the helical gear system. Therefore, the impact component should be more considered in the vibration reduction optimization of the high-speed helical gear system.
