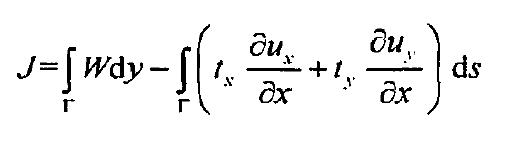As an important index of engineering fracture analysis, stress intensity factor is adopted by most scholars. The proposal of stress intensity factor is of great significance for the study of crack propagation direction. The research on stress intensity factor has been a hot issue for scholars all over the world. The correct solution is the most important. Scholars have adopted many methods to calculate this factor, such as engineering estimation method, finite element method, boundary element method, virtual crack propagation method, linear elastic method and photoelastic method. The above method can determine the stress intensity factor in most cases. However, in practical application, irregular parts and other complex situations may occur. In engineering problems, the analysis of structural parts are mostly in complex environment, which leads to the complexity of crack formation and propagation. At present, the determination of leading edge stress intensity factor of complex workpiece is still a hot issue in this field. In the continuous crack growth model, the primary problem is still the correct solution of the parameter factor. Because it is related to the accuracy of the results, it is essential.
The J-integral loop integral proposed by rice is shown in Figure 1. Its advantage is that its expansion path can be ignored. The J-integral can reflect the strength of the stress-strain field at the crack tip, and its definition expression is:
Where, R ends at any counterclockwise circuit on the lower and upper surface together; Ti is the stress component at any point of the primary circuit R; W-strain energy density at any point of loop R; N – unit vector of the outer normal direction on the loop R; UI – displacement component at any point of loop R; DS arc element on primary circuit R.
Previous research results show that in the case of on-line elasticity, the J integral, the crack propagation energy release rate, i.e. g, and the stress intensity factor, i.e. ruler, have the following formula:
Where, GR – plane stress, MPa; G1 – plane strain.
After the numerical simulation of the experiment, the J-integral is obtained through the post-processing, mapping path and other operations in ABAQUS. Then the stress intensity factor at the crack tip is obtained by the formula.
Figure 2 shows the crack length and crack tip stress intensity factor under different stress ratios. Under each stress ratio, the stress intensity factor has a linear relationship with the surrounding of a straight line and the crack length. It is positively proportional to the crack length. The simulation data confirm the above theoretical viewpoint. This corresponds to the Mises equivalent stress nephogram at the crack tip obtained in Fig. 3 and Fig. 4.
The data points were fitted linearly under different stress ratios. When the stress ratio r = 0.1, the slope of the fitting line between crack length and stress intensity factor data points is 1.52; When the stress ratio r = 0.6, the slope of the fitting line between crack length and stress intensity factor data points is 0.51. Comparing the slopes of different stress ratios, it can be seen that the smaller the stress is, the growth rate of stress intensity factor increases continuously with the increase of crack length.
When the crack length is a fixed value, the fitting line of small stress ratio (r = 0.1) is consistent above the figure. In contrast, the fitting line with large stress ratio (r = 0.6) is always below the graph. Compared with the two straight lines, the slope of the upper straight line is larger, so its growth rate is faster. Therefore, under the same abscissa, the difference between the two straight lines is increasing. The results show that when the stress ratio is small, the stress field intensity at the crack tip is higher, and the value of stress intensity factor does not expand in proportion to the stress ratio.