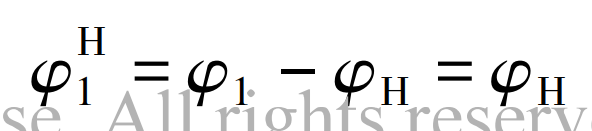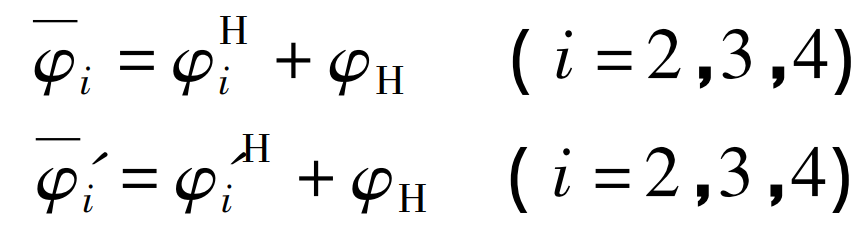Place the eccentric fixed shaft gear train in the gear box (planet carrier), and the center wheel 1 rotates in the same direction at twice the speed of the gear box, i.e ω 1 =2 ω H. A differential eccentric gear train with a degree of freedom of 2 is formed. Since the axes of the eccentric gear are parallel, according to the principle of relative motion, if a common angular velocity – ω H. Then the eccentric gear box is regarded as stationary, including:
The differential gear train can convert the fixed shaft gear train and the relative rotation angle of eccentric gears at all levels φ H2 、 φ H3 、 φ H4 、 φ’ 2H、 φ’ 3H and φ’ 4h can be obtained according to the formula. At this time, the absolute rotation angle of gears at all levels of differential eccentric gear system is:
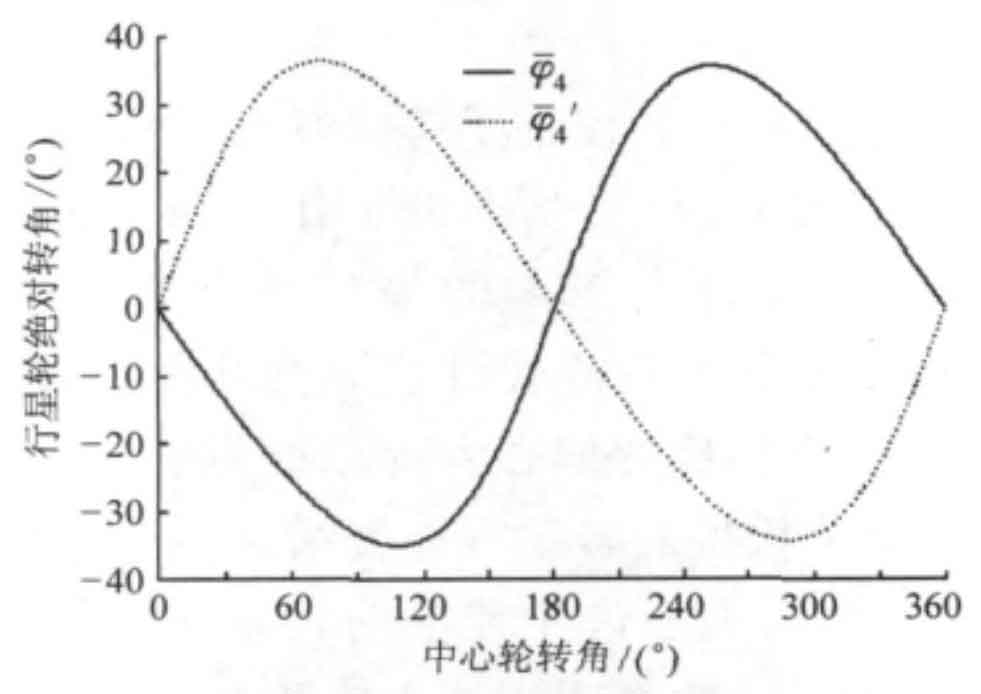
According to the formula, the absolute rotation angles of the positive and negative planetary gears 4 and 4 ‘of the differential eccentric gear train are shown in the figure. Different from the absolute rotation angle relationship of the bisection model, the absolute rotation angles of the positive and negative planetary gears under the bisection model do not show a centrosymmetric relationship at the 180 ° rotation angle of the first half cycle and the second half cycle.