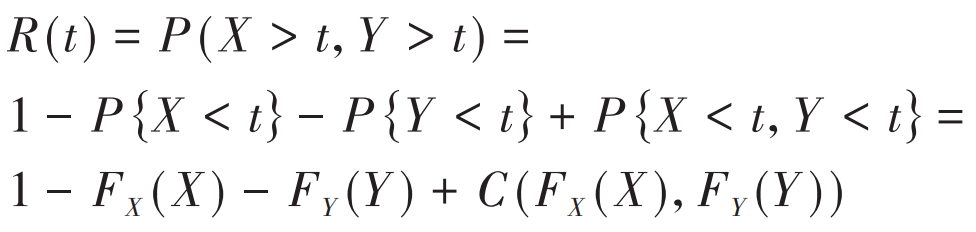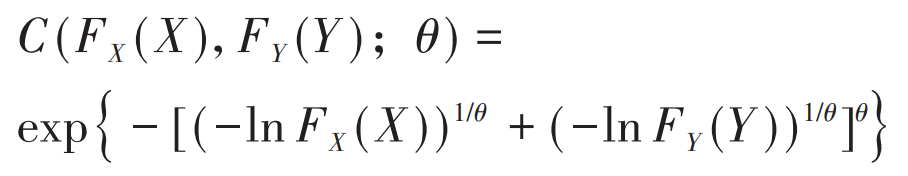Because the bevel gear transmission system has no redundant design, when the independent hypothesis is used for reliability analysis, the system reliability decreases rapidly with the increase of the number of series parts. However, the gears in the bevel gear transmission system are coupled through interaction, especially a pair of adjacent bevel gears directly participate in meshing, and there is a high statistical correlation between the load and the failure law. At this time, the error will occur when using the independent hypothesis model.
Therefore, by selecting the appropriate copula function, the dynamic reliability model of bevel gear transmission system considering failure correlation is constructed.
For a single bevel gear, there are two main failure modes: contact fatigue failure of bevel gear tooth surface and bending fatigue failure of tooth root. During operation, due to the same common cause load (CCF), there is a certain failure correlation between the failure modes of the system. For CCF in the system, Copula function can be used to describe the correlation between any random variables. At present, Archimedean copula function is widely used in the study of mechanical reliability considering failure correlation, and Gumbel copula function is suitable for long-life systems.
The corresponding edge distributions of the failure rates of bevel gear tooth surface contact fatigue failure and tooth root bending fatigue failure are FX (T) and FY (T). When considering the correlation between the two failure modes, the dynamic reliability of bevel gear is:
Substituting C (FX (x), FY (y)) into the expression of Gumbel copula function, we can get:
Where, C is the two-dimensional distribution function of Gumbel copula function; θ Is the correlation coefficient, and its value can be estimated by the kernel density nonparametric method. According to the formula, the dynamic reliability of bevel gear considering the correlation between contact fatigue and bending fatigue failure can be obtained.
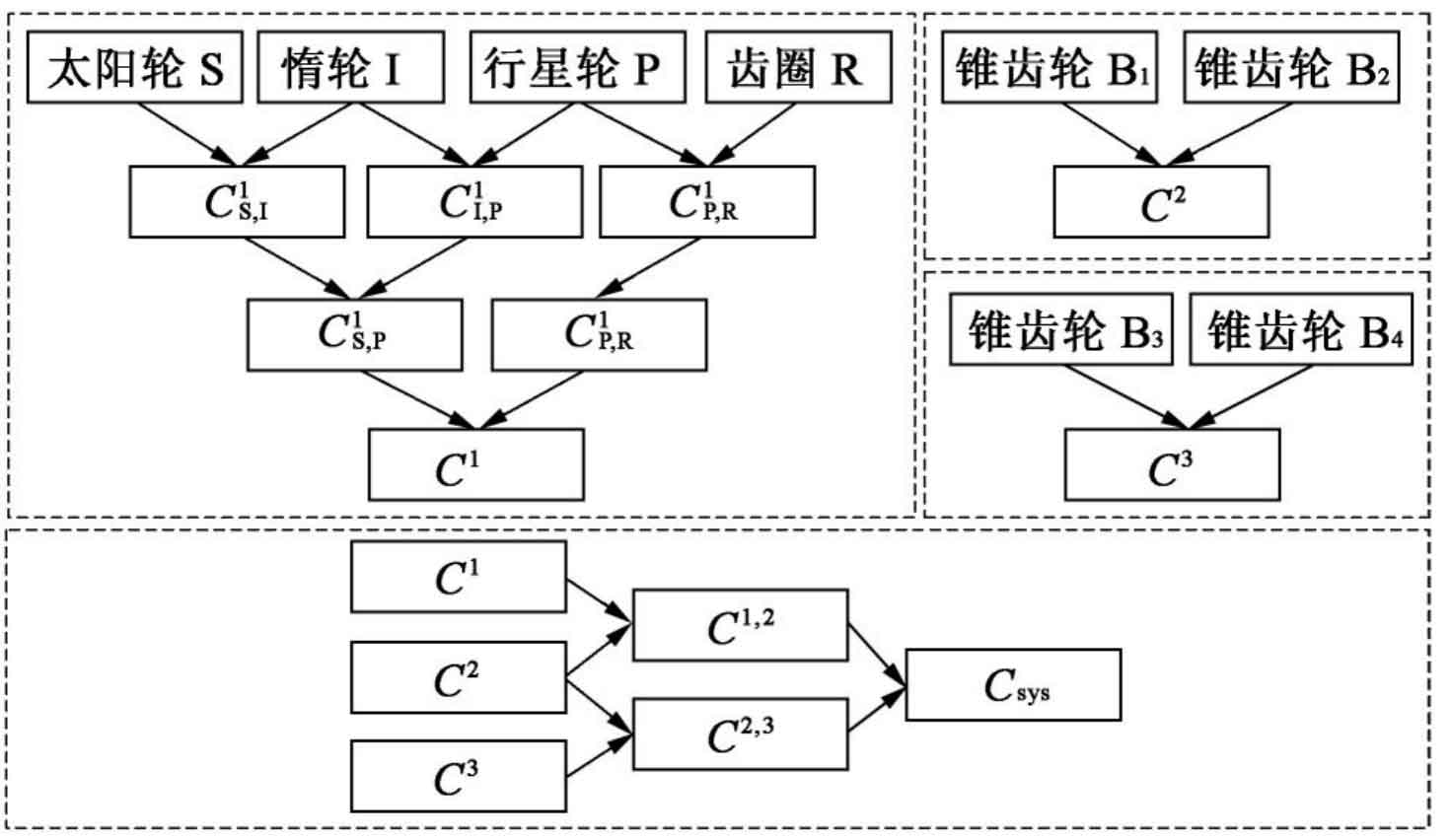
For the bevel gear transmission system of flying vehicle, it is formed by the coupling of multiple bevel gears. Directly using copula function for reliability modeling will lead to too high dimension and difficult to calculate. Therefore, in this paper, the analysis and modeling methods of “system level” and “system level” are used to split the whole transmission system into multiple subsystems. Firstly, the failure correlation between bevel gears in each subsystem is analyzed; Then the failure correlation between each subsystem layer is analyzed, and the reliability analysis model of the whole flight bevel gear transmission system is established. Schematic diagram of system level, in which C1, C2 and C3 represent the failure correlation functions of primary DSI planetary gear train, secondary bevel gear train and tertiary bevel gear train respectively.