As a developer specializing in gear design technology, I have dedicated significant effort to creating a comprehensive CAD system tailored for hypoid gears. Hypoid gears are crucial components in automotive differentials and industrial machinery, enabling efficient power transmission between non-parallel, non-intersecting shafts. Their complex geometry, characterized by offset axes and curved tooth profiles, demands precise design calculations and manufacturing adjustments. Traditional design methods rely heavily on manual chart lookups and iterative calculations, which are time-consuming and error-prone. To overcome these challenges, our team developed an integrated CAD system using modern programming tools, focusing on automation, accuracy, and user-friendliness. This system streamlines the entire process for hypoid gear design, from initial parameter selection to strength verification and drawing generation, ensuring that engineers can efficiently produce reliable hypoid gear sets for various applications.
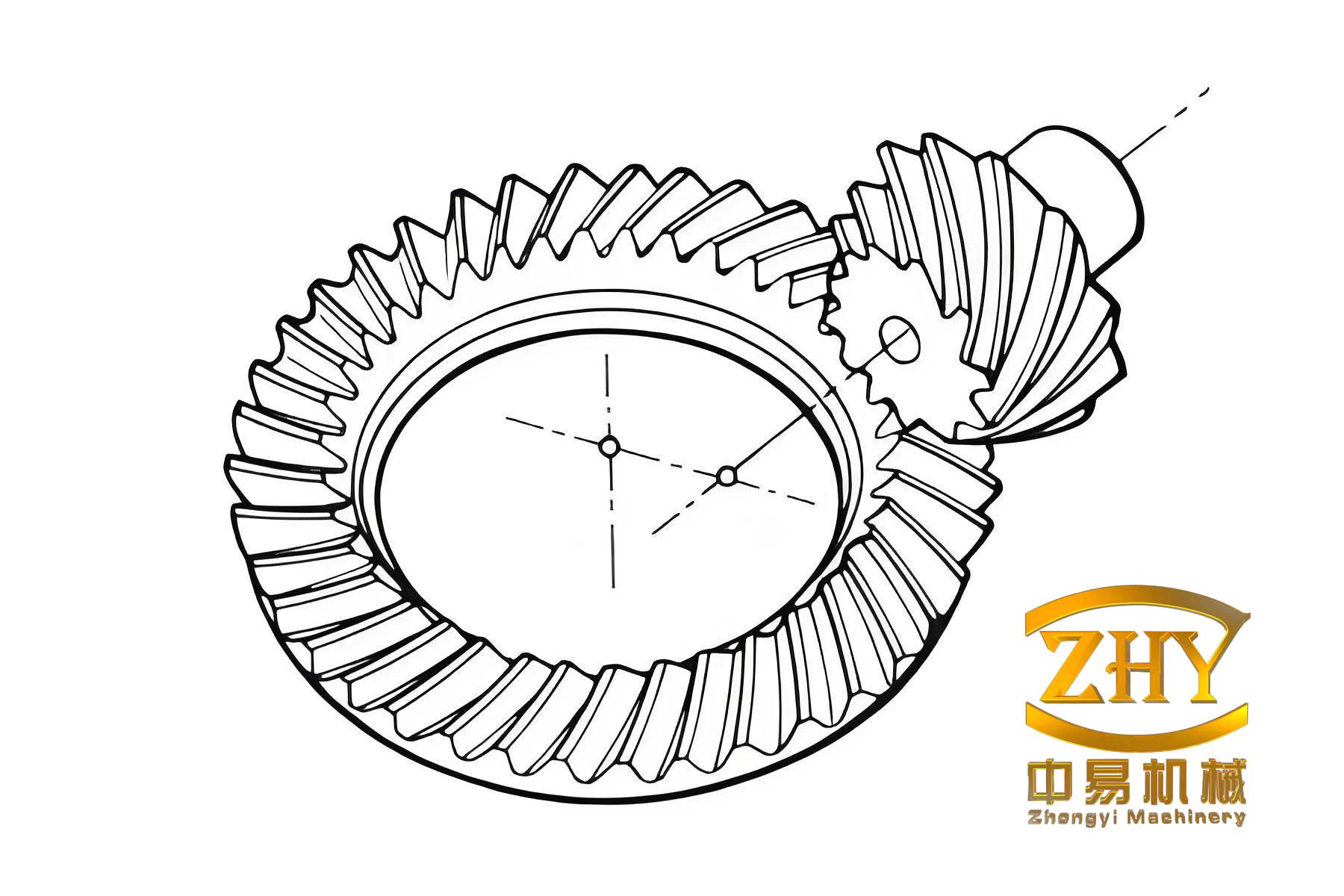
The development of this CAD system for hypoid gears was driven by the need to handle numerous parameters and charts programmatically. Hypoid gear design involves intricate relationships between geometric dimensions, cutting machine settings, and material properties. Our system leverages object-oriented programming in C++ along with AutoCAD’s ObjectARX 2000 toolkit to create a seamless environment where design calculations and parametric drawings are tightly integrated. In this article, I will detail the system architecture, module implementations, and key features, emphasizing how it addresses the specific demands of hypoid gear engineering. Throughout, I will use formulas and tables to summarize critical aspects, ensuring clarity and practicality for users involved in hypoid gear design.
The CAD system for hypoid gears is structured into four core modules: Gear Blank Design, Setting Calculation, Parametric Drawing, and Strength Verification. Each module addresses a distinct phase of the hypoid gear design workflow, and data flows between them to maintain consistency. The overall system architecture is depicted in Table 1, which outlines the inputs, processes, and outputs for each module. This modular approach allows for focused development and testing, ensuring that each component meets high standards of reliability. The use of C++ and ObjectARX enables direct interaction with AutoCAD, facilitating automatic drawing updates based on design parameters. By digitizing standard charts and implementing interpolation algorithms, the system reduces manual intervention, speeding up the design cycle for hypoid gears.
| Module Name | Primary Inputs | Core Processes | Key Outputs |
|---|---|---|---|
| Gear Blank Design | Number of teeth, module, pressure angle, spiral angle, shaft offset | Parameter validation, chart digitization, optimization for high-tooth design | Gear dimensions, tooth coefficients, cutter diameter selection |
| Setting Calculation | Gear dimensions, machine parameters, cutter specifications | Calculation of theoretical profile angles, machine roll ratio, cutter tilt | Adjustment cards for rough and finish cutting of both gears |
| Parametric Drawing | Gear dimensions, installation parameters (e.g., mounting distance) | ARX-driven drawing generation, dimensioning macros, data file integration | AutoCAD drawings of gear blanks, tooth profiles, and assembly views |
| Strength Verification | Gear dimensions, material properties, load conditions | Contact and bending stress calculations, chart-based coefficient fitting | Stress results, safety factors, redesign recommendations if needed |
The Gear Blank Design Module is the foundation of the CAD system for hypoid gears. It handles both standard and high-tooth designs, accommodating different industrial requirements. The module starts with 15 initial parameters, such as pinion teeth number $z_1$, gear teeth number $z_2$, normal module $m_n$, mean pressure angle $\alpha_n$, spiral angle $\beta$, and shaft offset $E$. These inputs are validated through range checks and dropdown lists to prevent errors. For instance, the mean pressure angle is selected from a combo box containing standard values like 20°, 22.5°, and 25°, which are common in hypoid gear applications. Tables for parameters like cutter diameter $D_c$ are digitized into arrays, allowing automatic retrieval based on the pitch diameter of the large gear $d_2$. The relationship is expressed as:
$$D_c = \begin{cases}
152.4 \, \text{mm} & \text{if } d_2 \leq 200 \, \text{mm} \\
203.2 \, \text{mm} & \text{if } 200 < d_2 \leq 300 \, \text{mm} \\
254.0 \, \text{mm} & \text{if } d_2 > 300 \, \text{mm}
\end{cases}$$
For values not explicitly listed, linear interpolation is used. The tooth height coefficient $h_a^*$ and addendum coefficient $c^*$ are optimized for high-tooth designs or selected from standard series for ordinary hypoid gears. The optimization aims to improve load capacity and noise reduction, critical for automotive hypoid gears. The gear blank dimensions are calculated using formulas derived from hypoid gear geometry. For example, the addendum diameter $d_a$ and dedendum diameter $d_f$ for the pinion are given by:
$$d_{a1} = d_1 + 2m_n h_a^* \cos \beta_1$$
$$d_{f1} = d_1 – 2m_n (h_a^* + c^*) \cos \beta_1$$
where $d_1$ is the pinion pitch diameter and $\beta_1$ is the pinion spiral angle. Similar formulas apply to the gear. The module also determines the face width $b$ based on the gear ratio and application requirements. Table 2 summarizes typical tooth height coefficients for hypoid gears under different design conditions, which are embedded in the system to guide users.
| Design Type | Gear Ratio Range | Pinion Teeth Count | Tooth Height Coefficient $h_a^*$ | Addendum Coefficient $c^*$ | Application Notes |
|---|---|---|---|---|---|
| Standard | 1:1 to 3:1 | 10-25 | 1.00 | 0.25 | General-purpose hypoid gears |
| Standard | 3:1 to 6:1 | 15-35 | 1.25 | 0.30 | High-torque hypoid gears |
| High-Tooth | 1:1 to 4:1 | 12-30 | 1.50 | 0.35 | Automotive differentials with noise reduction |
| High-Tooth | 4:1 to 8:1 | 20-40 | 1.75 | 0.40 | Industrial heavy-duty hypoid gears |
The Setting Calculation Module focuses on generating adjustment parameters for cutting machines, a critical step in manufacturing hypoid gears. This module computes values such as machine roll ratio $i_m$, cutter tilt angle $\delta$, and feed rates based on the gear blank dimensions and cutter specifications. The process begins with calculating theoretical tooth profile angles for the convex and concave sides of the hypoid gear teeth. These angles, denoted $\alpha_{conv}$ and $\alpha_{conc}$, are derived from the gear geometry and cutter geometry using the formula:
$$\alpha_{conv} = \alpha_n + \Delta \alpha \cdot \frac{R_c}{R_p}$$
$$\alpha_{conc} = \alpha_n – \Delta \alpha \cdot \frac{R_c}{R_p}$$
where $\Delta \alpha$ is a correction factor, $R_c$ is the cutter radius, and $R_p$ is the pitch radius of the gear. The results are displayed in the interface, allowing users to select actual cutter angles from standard values, ensuring compatibility with available tooling. The machine roll ratio $i_m$, which controls the relative motion between the cutter and gear during cutting, is calculated as:
$$i_m = \frac{z_2}{z_1} \cdot \frac{\cos \beta_2}{\cos \beta_1} \cdot K_r$$
where $z_1$ and $z_2$ are tooth numbers, $\beta_1$ and $\beta_2$ are spiral angles, and $K_r$ is a machine-specific coefficient typically from 0.95 to 1.05. The module outputs five adjustment cards: rough and finish cutting cards for both the pinion and gear, and a tooth gauge dimension card for quality control. Table 3 provides an example of adjustment parameters for a hypoid gear set with a 4:1 ratio, illustrating the detailed output that guides machinists.
| Parameter | Large Gear Rough Cut | Large Gear Finish Cut | Small Gear Rough Cut | Small Gear Finish Cut | Tooth Gauge Card |
|---|---|---|---|---|---|
| Cutter Diameter (mm) | 203.2 | 203.2 | 152.4 | 152.4 | N/A |
| Machine Roll Ratio | 3.85 | 3.85 | 1.45 | 1.45 | N/A |
| Cutter Tilt Angle (°) | 8.5 | 10.0 | 6.0 | 7.5 | N/A |
| Feed Rate (mm/rev) | 0.15 | 0.10 | 0.20 | 0.15 | N/A |
| Tooth Thickness (mm) | N/A | N/A | N/A | N/A | 5.25 ± 0.05 |
The Parametric Drawing Module automates the generation of AutoCAD drawings for hypoid gears, using a program-driven approach to ensure that dimensions update dynamically with design changes. This module is implemented as an ObjectARX application, which loads into AutoCAD and executes drawing commands based on data from the Gear Blank Design Module. The data is exchanged via text files containing key parameters like pitch diameters, tooth profiles, and installation settings. The parametric relationship for drawing a hypoid gear tooth profile is defined by a set of equations that convert design parameters into Cartesian coordinates. For a point on the tooth surface, the coordinates $(x, y, z)$ can be expressed as:
$$x = R \cos(\theta) + m_n \cdot h_a^* \cdot \sin(\beta) \cdot \cos(\theta + \phi)$$
$$y = R \sin(\theta) + m_n \cdot h_a^* \cdot \sin(\beta) \cdot \sin(\theta + \phi)$$
$$z = \frac{R \tan(\beta)}{\pi} \cdot \theta + m_n \cdot h_a^* \cdot \cos(\beta)$$
where $R$ is the pitch radius, $\theta$ is the angular position along the tooth, and $\phi$ is a phase angle dependent on the tooth number. This parametric model allows the drawing to adapt to any hypoid gear configuration. For dimensioning, macros simplify the code; for instance, the angular dimension macro ANG is defined in C++ as shown in the code snippet below, enabling quick placement of angle labels in drawings. The module also includes sub-modules for different drawing views, such as front, side, and isometric projections, ensuring comprehensive documentation for manufacturing.
#define ANG(p0, p1, p2, angle_value, p3) ads_command(RTSTR, "ANGULAR", RTSTR, "", RT3DPOINT, p0, RT3DPOINT, p1, RT3DPOINT, p2, RTSTR, "A", RTREAL, 0.0, RTSTR, "TEXT", RTSTR, angle_value, RT3DPOINT, p3, RTSTR, "", RTNONE)
The Strength Verification Module performs contact and bending stress analyses to ensure the hypoid gear set meets safety requirements under operational loads. This module uses standardized formulas adapted for hypoid gears, incorporating coefficients derived from digitized charts. The contact stress $\sigma_H$ is calculated using the ISO 6336-based formula modified for hypoid geometry:
$$\sigma_H = Z_E Z_H Z_\epsilon Z_\beta \sqrt{ \frac{F_t}{b d_1} \cdot \frac{u + 1}{u} }$$
where $Z_E$ is the elasticity coefficient (e.g., 189.8 $\sqrt{\text{MPa}}$ for steel pairs), $Z_H$ is the zone factor accounting for tooth curvature, $Z_\epsilon$ is the contact ratio factor, $Z_\beta$ is the spiral angle factor, $F_t$ is the tangential force, $b$ is the face width, $d_1$ is the pinion pitch diameter, and $u = z_2/z_1$ is the gear ratio. These factors are obtained from polynomial fits of chart data; for example, $Z_H$ for hypoid gears is approximated as:
$$Z_H = 0.85 + 0.15 \cdot \left( \frac{\beta}{45^\circ} \right) – 0.02 \cdot \left( \frac{\beta}{45^\circ} \right)^2$$
The bending stress $\sigma_F$ is computed similarly, with factors for tooth root geometry. The module validates the design by comparing stresses to allowable limits based on material properties, such as those in Table 4. If stresses exceed limits, the system prompts redesign with adjusted parameters, ensuring robust hypoid gear performance.
| Material Grade | Elastic Modulus $E$ (GPa) | Poisson’s Ratio $\nu$ | Allowable Contact Stress $\sigma_{H,\text{lim}}$ (MPa) | Allowable Bending Stress $\sigma_{F,\text{lim}}$ (MPa) | Typical Use in Hypoid Gears |
|---|---|---|---|---|---|
| 20MnCr5 (Case-Hardened) | 210 | 0.3 | 1500 | 450 | Automotive differentials |
| 42CrMo4 (Through-Hardened) | 210 | 0.3 | 1200 | 400 | Industrial gearboxes |
| GGG40 (Ductile Iron) | 170 | 0.275 | 800 | 300 | Low-load applications |
| Aluminum 7075-T6 | 71 | 0.33 | 500 | 200 | Aerospace hypoid gears |
The CAD system for hypoid gears emphasizes interactivity, parametrization, and standardization to enhance usability and reliability. The user interface is built with dialog boxes and controls like combo boxes and radio buttons, allowing intuitive parameter selection. For example, when inputting the spiral angle for a hypoid gear, users choose from common values (e.g., 35°, 40°, 45°) in a dropdown list, reducing input errors. Parametrization is central to the system; all modules share variable parameters, so changes in one module propagate automatically. For instance, modifying the shaft offset $E$ updates the gear blank dimensions, adjustment calculations, drawings, and strength checks, ensuring data consistency across the hypoid gear design process. Standardization is achieved by embedding industry standards, such as AGMA or ISO guidelines, into the code. Simple tables are digitized as arrays, while extensive data (e.g., tolerance tables) are stored in external databases accessed via ODBC connections. This hybrid approach balances performance and maintainability for hypoid gear design.
To further improve the CAD system for hypoid gears, we implemented features like context-sensitive help and input validation. The help system explains parameter meanings and design guidelines for hypoid gears, aiding less experienced users. Input validation includes range checks and automatic corrections; for example, if a user enters a cutter tip radius $r_t$ of 0.23 mm, the system rounds it to 0.25 mm, as standard cutters come in multiples of 0.25 mm for hypoid gear manufacturing. These features reduce trial-and-error and accelerate the design cycle. Additionally, the system supports batch processing for multiple hypoid gear designs, useful in production environments where variations of gear sets are needed.
In conclusion, the developed CAD system for hypoid gears represents a significant advancement in gear design technology. By integrating C++, ObjectARX, and AutoCAD, it provides a cohesive platform that automates tedious tasks while maintaining flexibility for customization. The system has been validated through industrial trials, demonstrating its ability to produce accurate hypoid gear designs and manufacturing instructions efficiently. Future enhancements could include integration with CNC programming for direct machine control or incorporation of finite element analysis for advanced stress simulation. Ultimately, this CAD system empowers engineers to tackle the complexities of hypoid gear design with confidence, contributing to improved performance and reliability in applications ranging from vehicles to industrial machinery. The ongoing evolution of hypoid gear technology will benefit from such integrated tools, ensuring that design processes keep pace with manufacturing advancements.
