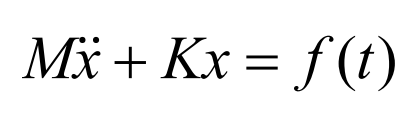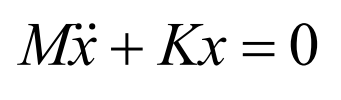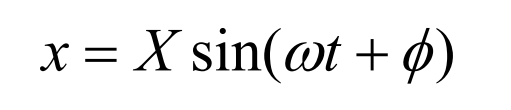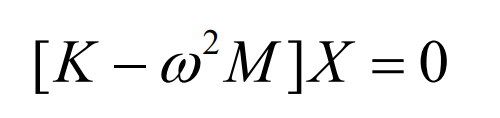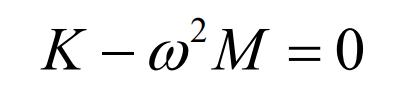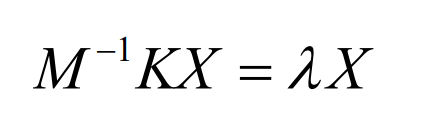The vibration characteristics of mechanical system can usually be described by the natural frequency and vibration mode of the system.
The differential equation of undamped vibration system is expressed as:
Where, M is the mass matrix of the system and is a positive definite matrix; K is the stiffness matrix of the system, which is n × N-order real symmetric matrix; F (T) is the incentive term.
Then the differential equation of free vibration of the system is:
The solution of free vibration system is:
Substitute the formula to obtain:
The condition that the above formula has non-zero solution is:
The formula is the characteristic equation of the system, from which n positive real roots can be obtained ω I2, then ω I is the natural frequency of the system.
Order λ=ω 2. Then the main vibration mode equation can be reduced to:
According to the above method, the system equation can obtain n natural frequencies and N main vibration modes. Each pair of frequencies and vibration modes represent the vibration of one degree of freedom of the system, and the free vibration of multi degree of freedom system is the superposition of N simple harmonic vibration of single degree of freedom.