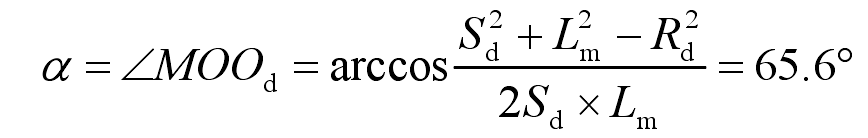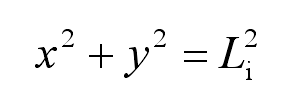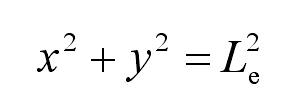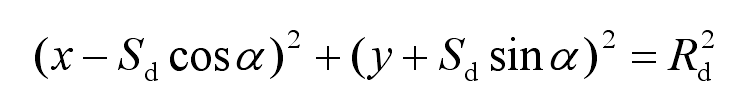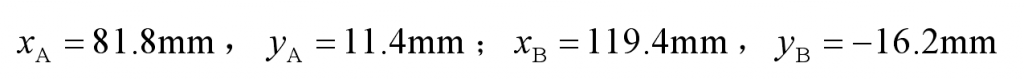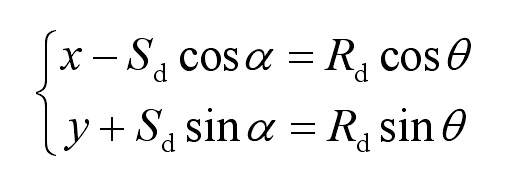As can be seen from Figure 1, the shape of spiral bevel gear is relatively complex, especially its tooth shape is spiral curved teeth, and does not meet the axisymmetric conditions, so it is impossible to directly analyze the forging deformation force required for its forming by the above methods. Therefore, it is very necessary to simplify the tooth profile of spiral bevel gear. In the precision forging of spiral bevel gear, the existence of spiral teeth only has a torque to the tooth die bore in the horizontal direction, but does not increase the deformation force required for its forming in the vertical direction. Therefore, according to the principle that the volume of the deformed body remains unchanged before and after plastic deformation, the spiral curved teeth can be simplified into linear teeth. At the same time, considering the convenience of solving the cross-sectional area of tooth profile, the involute tooth profile is simplified into linear tooth profile according to the principle of equal area.
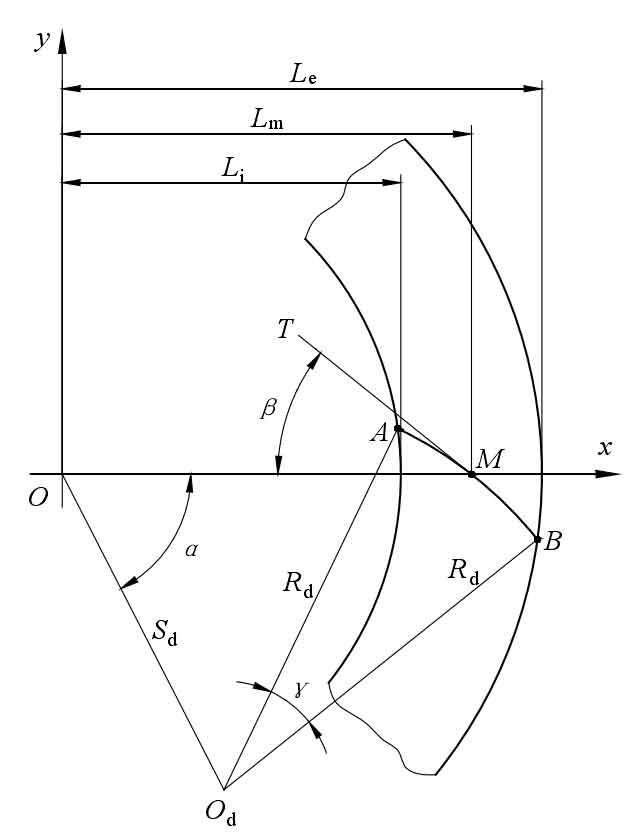
Fig. 2 is an expanded view of the pitch cone of the spiral bevel gear. In the figure, O is the center of the plane gear, OD is the center of the cutter head, AB is the pitch line of the tooth surface, M is the center of the pitch line of the tooth surface, ∠ β Is the central helix angle.
In △ mood, ∠ α The value of is:
The circular equation of the small end of the tooth profile of the spiral bevel gear is:
The circle equation of the large end of the tooth profile of spiral bevel gear is:
The equation of the outer circle of the cutter head is:
According to the simultaneous formula, the coordinates of points a and B are respectively:
Substitute into the formula :