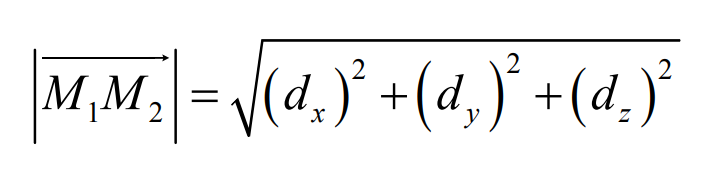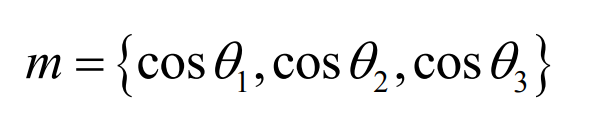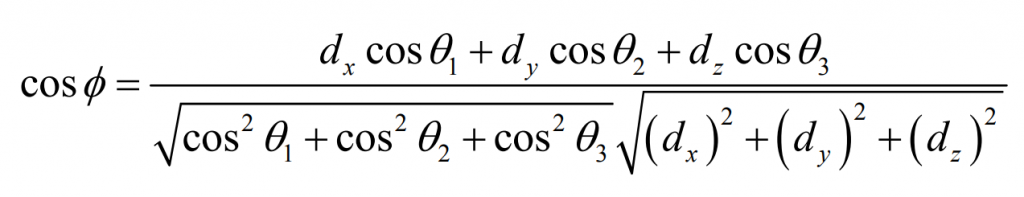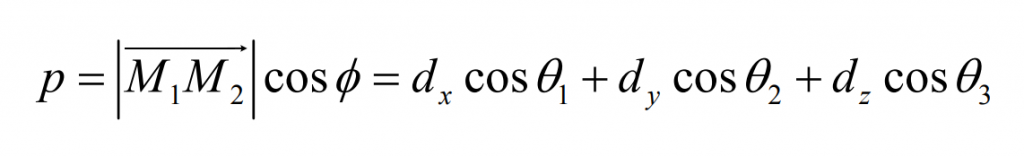When measuring the tooth surface of logarithmic spiral bevel gear, there is an error between the theoretical value and the actual measured value of the tooth surface data point. The vectors of the theoretical point and the actual measured point do not necessarily coincide with the normal vector passing through the theoretical point. The normal deviation is the projection of the vector from the theoretical point to the actual measured point in the normal direction. Taking the theoretical point M1 (x1, Y1, z1) as the starting point and the actual measuring point M2 (X2, Y2, Z2) as the end point, the difference between the actual measured value and the theoretical value on the three coordinate axes of X, y and Z is x, y and Z respectively:
The included angle between the normal vector of the tangent plane passing through the point and the positive direction of the three coordinate axes x, y and Z is set respectively θ 1 , θ 2 , θ 3. The direction cosine of the normal vector is cos θ 1 , cos θ 2 , cos θ 3. The unit vector m (pointing out of the tooth surface) whose direction is consistent with the normal direction passing through the point is:
Then the angle between the vector and the vector φ The cosine of is:
The normal deviation P of the tooth surface of logarithmic spiral bevel gear is the projection of the vector on M, which is equal to the modulus multiplied by the angle between the vector and m φ Cosine of:
If cos φ If it is positive, then 0 ≤ φ ≤ 90 °, the normal deviation P is positive, and the actual measurement point is outside the point, indicating that the part processing is large; If cos φ If it is negative, then 90 °< φ ≤ 180 °, the normal deviation P is negative, and the actual measuring point is on the inner side of the point, indicating that the part processing is small; After the normal deviation is obtained, the tooth surface difference surface of logarithmic spiral bevel gear can be obtained according to the normal deviation.