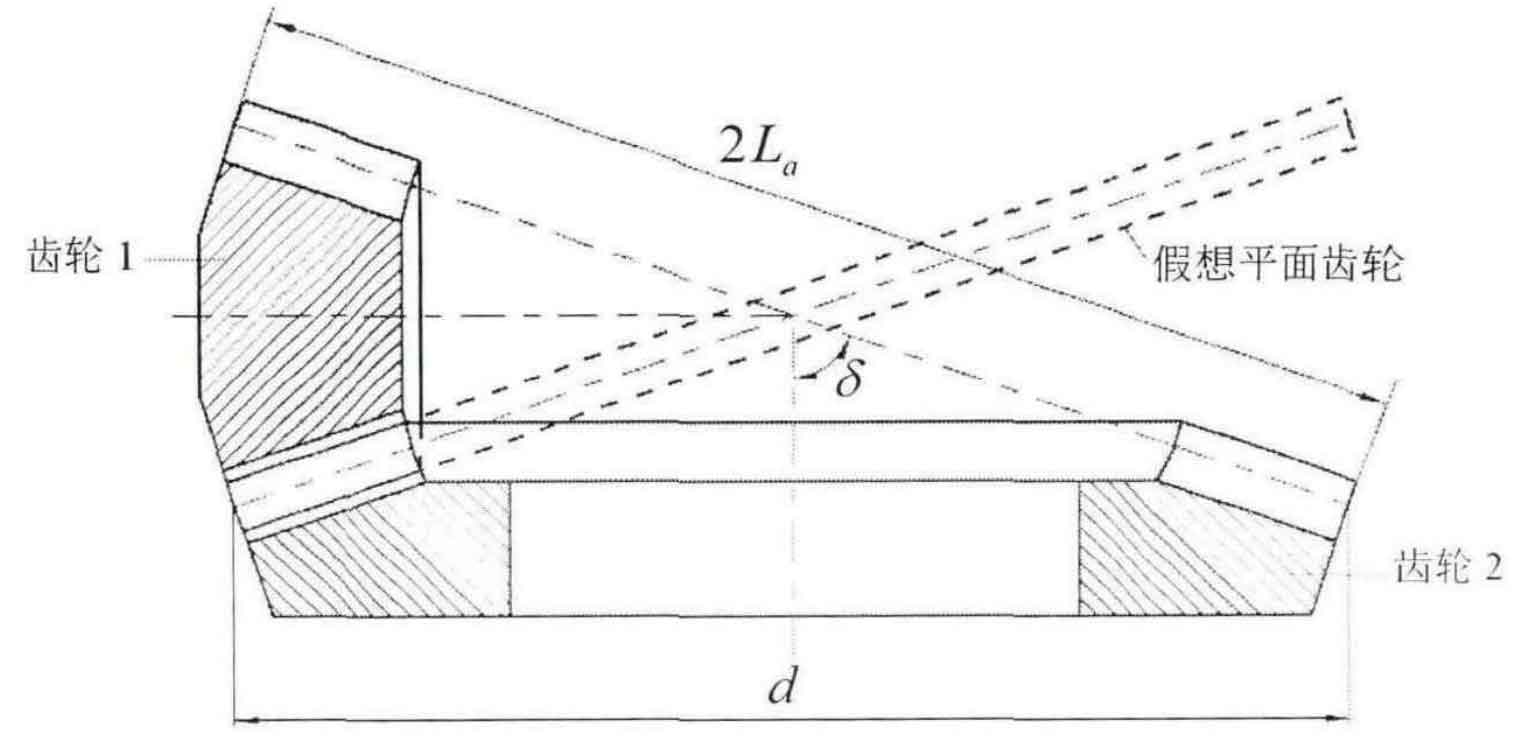
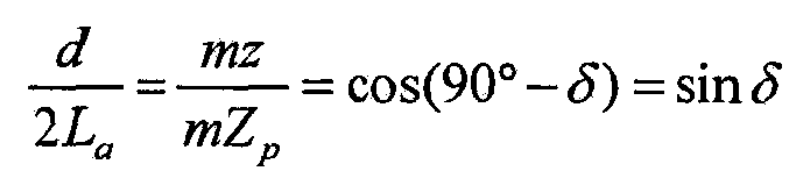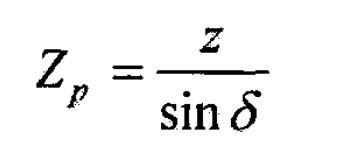When using milling cutter for machining equal height spiral bevel gear, the gear cutting principle is the imaginary plane gear model. Therefore, calculating the number of teeth of the imaginary plane gear and modeling the equal height spiral bevel gear play an important role.
The imaginary plane gear is obtained by unfolding the equal height spiral bevel gear along the pitch cone bus, so the imaginary plane gear and the equal height spiral bevel gear can be meshed and transmitted. According to the meshing principle of spiral bevel gear, the imaginary plane gear and equal height spiral bevel gear have the same modulus, and the radius of the imaginary plane gear is equal to the large end pitch of the equal height spiral bevel gear. The axes of equal height spiral bevel gears intersect and are perpendicular to each other, so the large wheel and the small wheel have the same pitch and helix angle. Therefore, the imaginary plane gear obtained by expanding the large wheel and the small wheel along the section conical bus is consistent.
The imaginary plane gear is obtained by unfolding the equal height spiral bevel gear along the pitch cone bus, so the imaginary plane gear and the equal height spiral bevel gear can be meshed and transmitted. According to the meshing principle of spiral bevel gear, the imaginary plane gear and equal height spiral bevel gear have the same modulus, and the radius of the imaginary plane gear is equal to the large end pitch of the equal height spiral bevel gear. The axes of equal height spiral bevel gears intersect and are perpendicular to each other, so the large wheel and the small wheel have the same pitch and helix angle. Therefore, the imaginary plane gear obtained by expanding the large wheel and the small wheel along the section conical bus is consistent.
It is known that the large end modulus of equal height tooth spiral bevel gear is m, the number of teeth is Z, and the pitch cone angle is δ , Then the diameter of the large end pitch circle d = MZ, and the modulus of the imaginary plane gear is also M. And because the radius of the imaginary plane gear is the same as the large end pitch l of the spiral bevel gear with equal height teeth α Equal, and assuming that the diameter of the plane gear is MZP, it can be obtained from the triangular relationship:
Then the number of teeth of the hypothetical plane gear is: