Take the traction spur gear of a certain type of locomotive as an example to calculate the actual coincidence before and after flange repair. The rated power of the single axle of the locomotive is 1130kW, the speed under continuous operation condition is 48.6km/h, the motor speed is 1034r/min, the speed under high speed condition is 116km/h, the motor speed is 2553r/min, and the basic parameters of the spur gear are shown in Table 1.
| Name | Wheel | Pinion |
| Modulus m | 12 | 12 |
| Pressure angle of indexing circle α | 25 | 25 |
| Helical angle of indexing circle β | 0 | 0 |
| Top clearance coefficient c* | 0.35 | 0.35 |
| Number of teeth z | 16 | 77 |
| Center distance a | 565 | 565 |
| Modification coefficient x | 0.228 | 0.37165 |
| Base node error fpb | 0.016 | 0.018 |
The mainstream G. Niemann formula is a calculation method for the actual coincidence degree proposed considering the influence of meshing deformation. Its formula is:
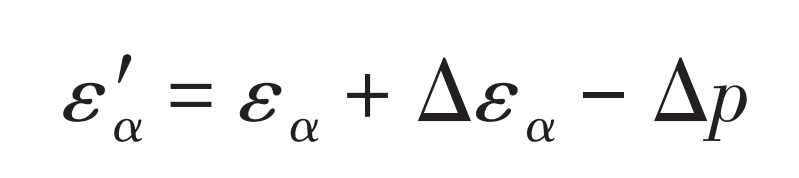
Where: εα— Theoretical coincidence degree; Δεα— The increase of coincidence caused by meshing deformation is selected according to the load and spur gear structure (0.15~0.25); Δ P – root mean square error of base pitch of two gear teeth, namely:
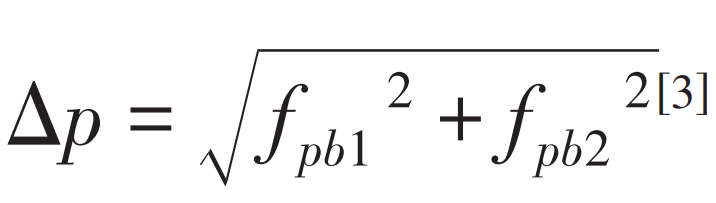
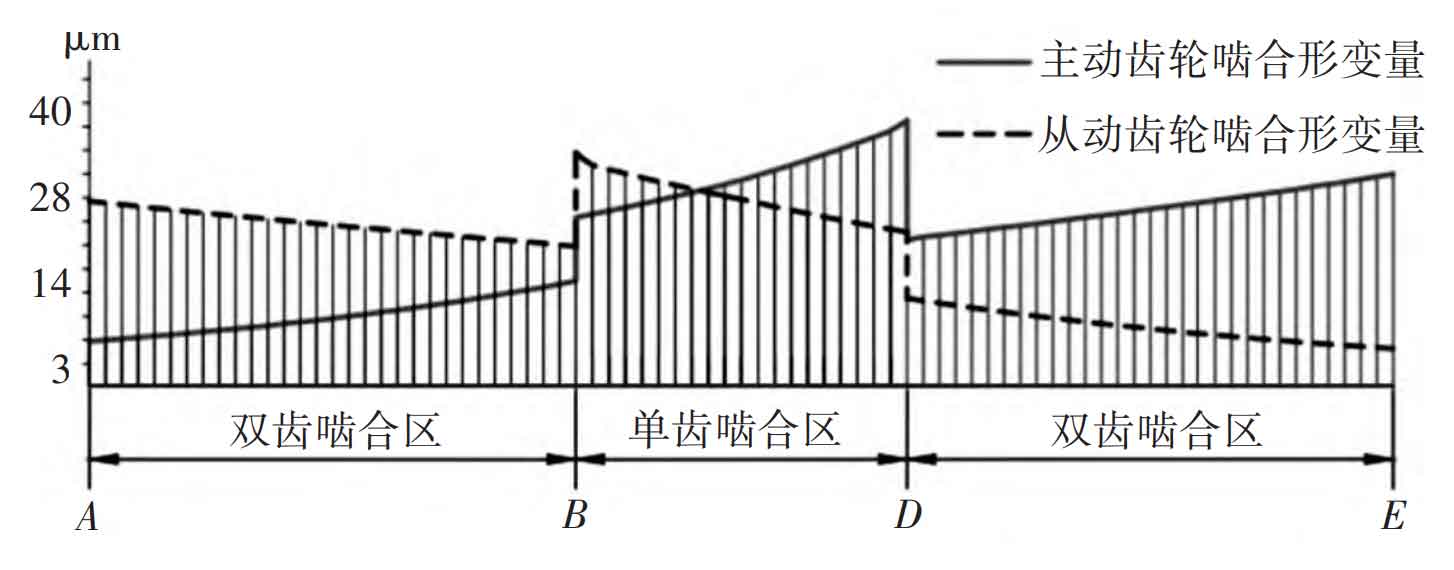
In this instance, Δεα Take 0.15, Δ P=0.03, theoretical coincidence according to the existing formula εα Is 1.38625, and the actual coincidence is calculated by the formula ε′α Is 1.50625. When the above method is used to solve the actual coincidence, the meshing shape variables of the driving and driven gears and the tooth meshing process shape variables under continuous working conditions are first solved according to Ishikawa formula and the load distribution relationship between teeth, as shown in Figure 1. The meshing shape variables of the driving gear and the driven gear at the alternating point of single and double teeth are respectively δ B=0.0641 and δ D = 0.0621。
Determine the trimming tolerance zone of the driving and driven gears according to the elastic deformation formula, as shown in Figure 2. When the straight-line modification method is adopted, according to the design principle of the optimum amount of the tooth top, the trimming curve is obtained by taking the starting point of the modification as the local coordinate origin:
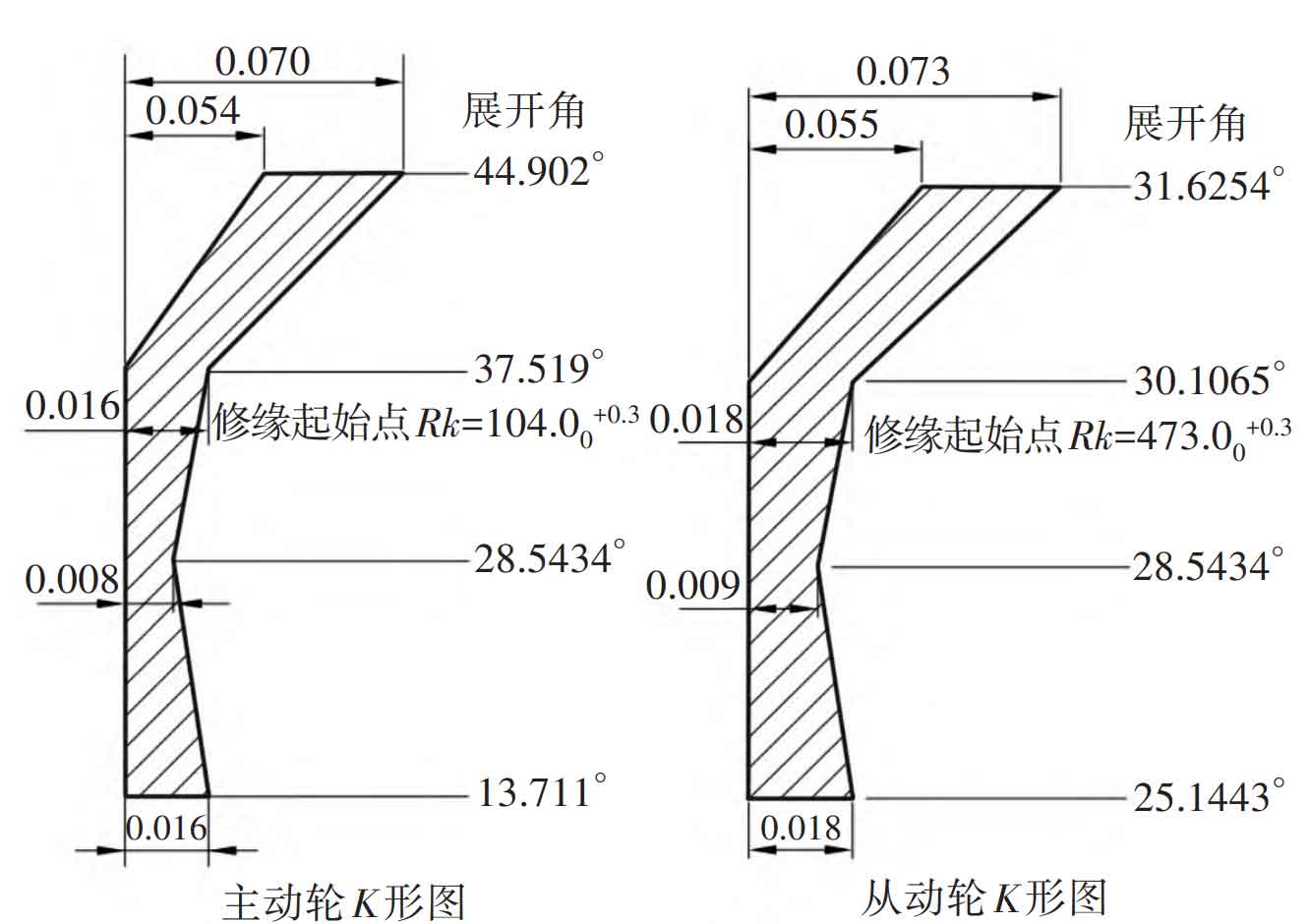
The curve equation of spur gear driving wheel trimming is:
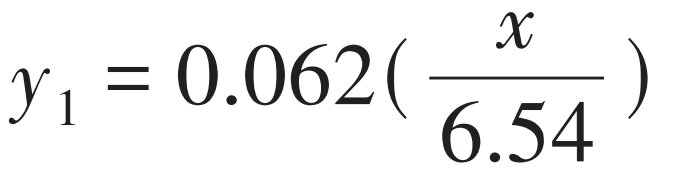
The curve equation of spur gear driven wheel trimming is:
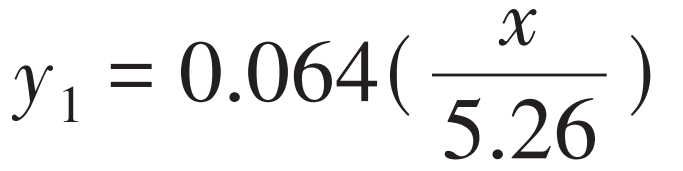
Calculate the theoretical coincidence degree according to the above analysis εα It is 1.38625, and the actual coincidence degree under continuous working condition after trimming is increased to 1.44235, and the change trend is consistent with G. Niemann formula. The actual coincidence degree under high-speed working condition is reduced to 1.21355 because the shape variable is less than the trimming amount. Since the influence of the relative relationship between the trimming amount and the deformation amount on the coincidence degree is not considered in the G. Niemann formula, its calculation result is greater than that obtained by the method here. The comparison of the specific calculation results is shown in Table 2.
| Coincidence degree | G. Niemann method | Use method |
| Theoretical coincidence | 1.38625 | 1.38625 |
| Continuous working condition coincidence | 1.50625 | 1.44235 |
| High-speed working condition coincidence | 1.50625 | 1.21355 |
