The dividing circle diameter of driving wheel of locomotive traction gear is 324 mm, transmission ratio μ = 2.59, tooth width coefficient diameter d = 0.53. Through calculation, the torque T1 = 4 168 030 n · mm can be obtained, and the elastic influence coefficient Ze = 189.8 mpa1 / 2, and the area influence coefficient zh = 2 / (sin α cos α) = 2.38. The above parameters are substituted into the formula, and the driving wheel diameter is calculated to be 254 The relative error between the theoretical calculation value and the actual gear size is 22%.
Taking the allowable film thickness ratio [λ] = 3, according to the strength design formula of non Hertz contact gear, the diameter of driving wheel is 321 mm. Compared with the actual diameter of gear, the difference is only 3 mm, and the relative error is only 0.9%. The theoretical design value and the actual size of the gear are in good agreement. The results show that the gear transmission not only meets the strength requirements, but also meets the requirements of elastohydrodynamic lubrication.
The high-speed and heavy-duty gears used in high-speed locomotives, airplanes and ships should not only have sufficient bending strength of tooth root and contact strength of tooth surface, but also have enough anti scuffing ability. Therefore, according to the winter integral temperature method in GB / t6413-1986, according to the actual size of the gear, the design size based on Hertz theory and the design size based on non Hertz contact theory, the anti scuffing ability of the gear is checked and compared.
Integral criterion:
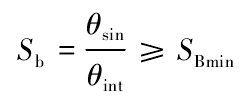
Where sb is the anti scuffing safety factor; θ sin is the bonding temperature, ℃; θ int is the integral temperature, ℃; and sbmin is the minimum safety factor against scuffing.
The minimum safety factor of anti scuffing bearing capacity of gear is sb ≥ 1.5.
The safety factor of actual gear is SBR = 3.38; the safety factor of gear designed based on Hertz theory is SBH = 0.98; the safety factor of gear designed based on non Hertz contact theory is sbnh = 3.19.
The calculation results show that the gear designed based on Hertz theory does not meet the requirements of anti scuffing bearing capacity, but the actual gear meets the requirements of anti scuffing bearing capacity. The gear designed according to the non Hertz contact theory not only meets the requirements of strength and EHL, but also meets the requirements of scuffing bearing capacity. From the point of anti scuffing ability, the design results of the theory in this paper are also in good agreement with the actual gear.
