In the nonlinear dynamic model of yaw-torsion coupling, there are two main factors affecting the yaw vibration, i.e. the bias moment caused by uneven distribution of tooth loads and the gyroscopic moment caused by the change of space orientation of the rotating shaft. Among them, the bias moment increases with the increase of dynamic meshing force and the gyroscopic moment increases with the increase of rotational speed.
The main purpose is to analyze the influence of yaw vibration at different speeds on the dynamic load of gears.Two dynamic models are used: the first model is the yaw-torsion coupling non-linear dynamic model proposed in this paper; the second model is the yaw-torsion coupling non-linear dynamic model, in which the degree of swing freedom is neglected. The dynamic engagement forces of both models are calculated using the proposed non-linear dynamic engagement model.
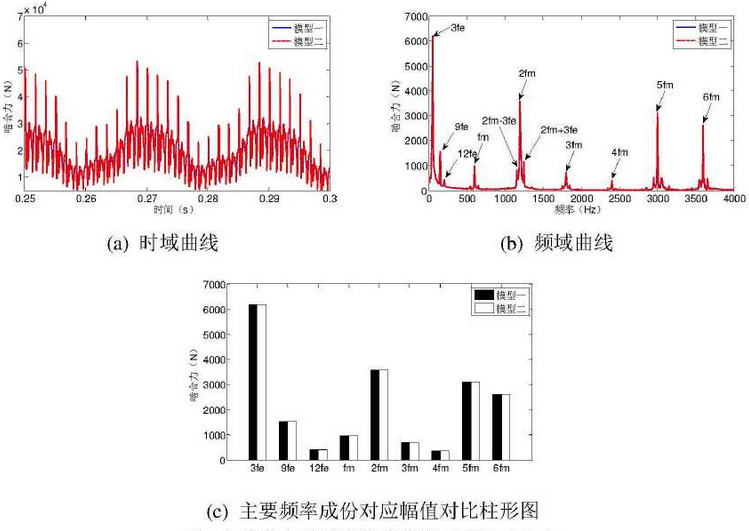
The time-domain and frequency-domain curves of the dynamic engagement forces of the two models are shown in the diagram for the engine at the lowest full throttle speed of 1000 r/min.It can be seen from the diagram that the time-domain and frequency-domain curves of the dynamic engagement force of the two models coincide basically, and the maximum dynamic engagement force is 53538N.The time-domain and frequency-domain curves of the dynamic engagement force of the two models are shown in the diagram for the engine at 4200r/min of full throttle rated speed.It can be seen from the diagram that there is little difference between the dynamic engagement forces of the two models, the maximum dynamic engagement forces are 45701N and 45728N respectively, and the error between them is only 0.6%.
At the above two speeds, the frequency components of dynamic engagement force of both models are mainly engine excitation frequency, engagement frequency and frequency multiplication.At the same time, due to the modulated side band characteristics of dynamic meshing force, their combined frequencies with engine excitation frequency appear near the meshing frequency and its frequency multiplication.It can be seen from the charts and graphs that there is little difference between the amplitudes of the two models in terms of the main frequency components of meshing force.
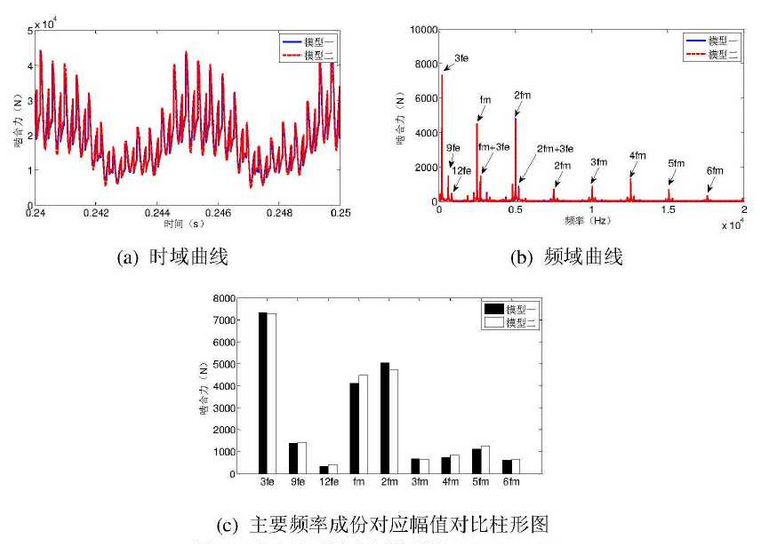
The above analysis shows that for heavy-duty vehicle gear drive system, the influence of swing vibration on dynamic load is small and can be ignored.Especially when modeling and solving complex multi-stage gear drive system in heavy-duty vehicles, the degree of freedom of the system’s yaw-torsion coupling nonlinear dynamic model is more, which greatly affects the calculation efficiency. The influence of the yaw vibration can be ignored while ensuring the calculation accuracy and considering the calculation efficiency.
