In mechanical transmission systems, screw gear drives, commonly known as worm drives, play a pivotal role due to their ability to provide high reduction ratios, compact design, and smooth operation. However, the presence of backlash—the clearance between non-working tooth surfaces—can lead to issues such as positioning errors, reduced accuracy, and diminished dynamic response in systems requiring frequent reversals. To address these challenges, backlash-adjustable screw gear drives have been developed, allowing for the minimization or elimination of backlash, thereby enhancing precision and longevity. This article reviews the various types of backlash-adjustable screw gear drives, classified by their adjustment principles, discusses their characteristics, and predicts future trends. The term “screw gear” is used throughout to refer to worm gear mechanisms, emphasizing the helical engagement that defines these drives.
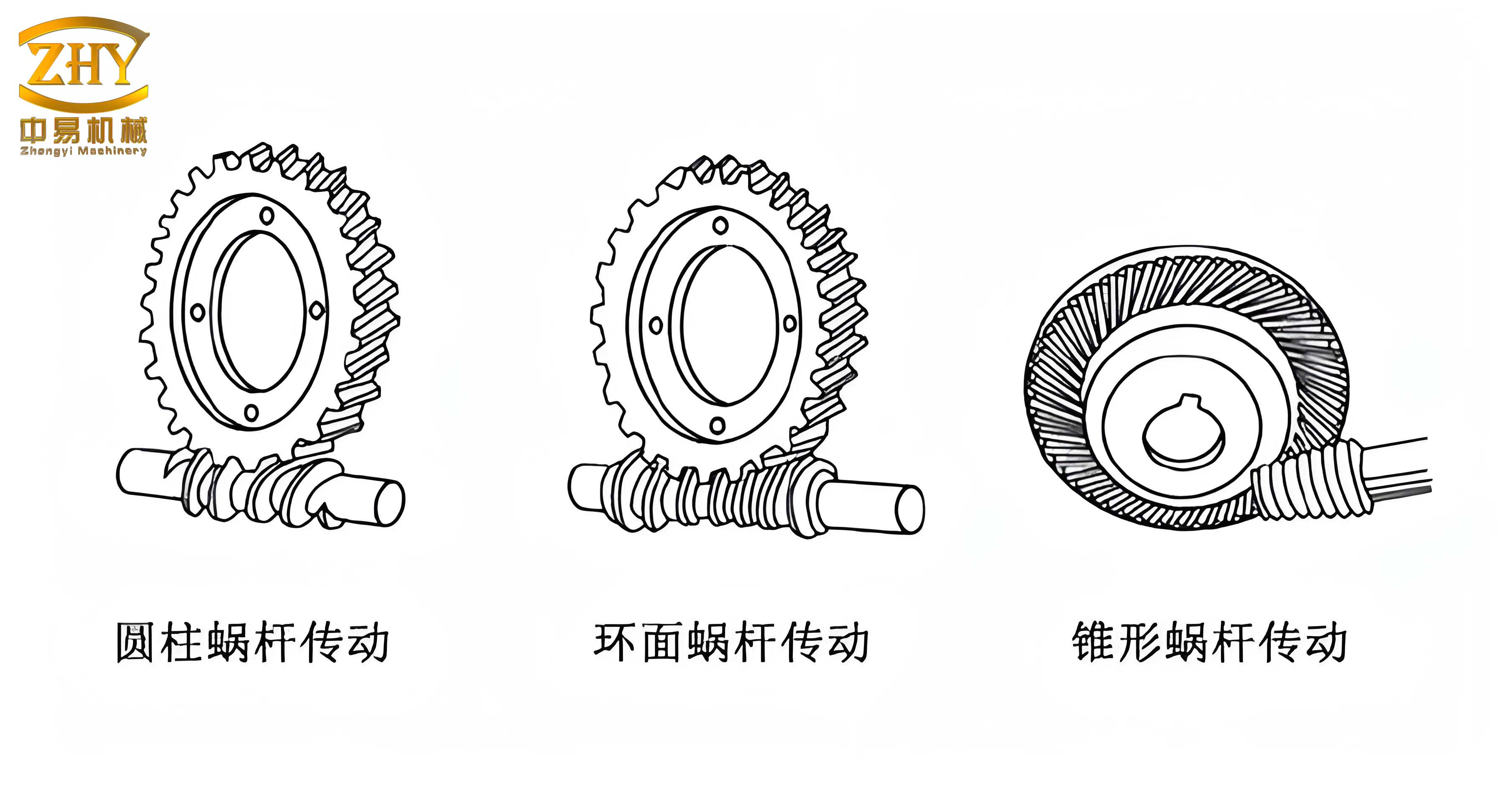
Screw gear drives are integral in applications like industrial robots, CNC machines, radar systems, and precision instruments, where high positional accuracy and stability are paramount. Backlash in these drives arises from manufacturing tolerances, wear, and thermal expansion, and while necessary to prevent jamming and accommodate lubrication, it can compromise performance. Adjustable backlash mechanisms enable compensation for wear and fine-tuning of clearance, making screw gear drives suitable for high-precision tasks. This review explores the fundamental principles behind backlash adjustment in screw gear drives, highlighting the mathematical relationships and practical implications. The classification is based on the method of adjustment: center distance modification, axial movement of the screw, circumferential rotation of the screw, axial movement of the gear, and circumferential rotation of the gear. Each category is analyzed with formulas and tables to summarize key aspects.
The importance of screw gear drives in modern engineering cannot be overstated. They offer transmission ratios ranging from 5:1 to over 1000:1 in a single stage, making them ideal for applications where space is limited. However, the inherent sliding contact in screw gear drives leads to friction and wear, which gradually increases backlash over time. Adjustable designs mitigate this by allowing periodic readjustment, thus maintaining performance. In this article, I will delve into the mechanics of each adjustment type, providing insights into their advantages and limitations. The discussion is framed from a first-person perspective, drawing on general engineering principles to ensure clarity and applicability. By emphasizing the term “screw gear,” I aim to reinforce the focus on these versatile transmission elements.
Classification of Backlash-Adjustable Screw Gear Drives
Backlash-adjustable screw gear drives can be categorized into five main types based on the adjustment principle. Each type involves specific modifications to the screw, gear, or their assembly to control clearance. Below, I describe these categories in detail, including the mathematical relationships for backlash adjustment and compensation. A summary table is provided to compare their features.
| Adjustment Principle | Type of Screw Gear Drive | Key Adjustment Mechanism | Backlash Compensation Formula | Advantages | Disadvantages |
|---|---|---|---|---|---|
| Center Distance Adjustment | Standard Cylindrical Screw Gear | Moving screw along center distance direction | $$ \delta = 2h \tan \alpha $$ | Simple structure, low cost | Poor contact pattern, accelerated wear |
| Axial Movement of Screw | Dual-Lead Cylindrical Screw Gear | Axial displacement of screw with unequal lead on tooth flanks | $$ \delta = 2h \frac{P_2 – P_1}{P_1 P_2} $$ | Precise adjustment, no change in mesh geometry | Complex manufacturing, limited load capacity |
| Axial Movement of Screw | Conical Screw Gear (Spiroid Drive) | Axial displacement of conical screw | $$ \delta = h \cos \beta (\tan \alpha_1 + \tan \alpha_2) $$ | Multiple tooth contact, good lubrication | Asymmetric pressure angles, root cutting risk |
| Circumferential Rotation of Screw | Split Screw Gear Drive | Relative rotation of split screw halves | $$ \delta = \frac{h P}{2\pi} $$ | Easy adjustment, maintained contact | Reduced load capacity, complex assembly |
| Axial Movement of Gear | Variable Tooth Thickness Planar Gear Enveloping Screw Gear | Axial displacement of wedge-shaped gear | $$ \delta = h \tan(|\beta_1 – \beta_2|) $$ | High precision, wear compensation | Requires run-in after adjustment |
| Axial Movement of Gear | Variable Tooth Thickness Involute Gear Enveloping Screw Gear | Axial displacement of gear with unequal spiral angles | $$ \delta = 2h \frac{\tan \psi_1 \tan \psi_2}{\tan \psi_1 + \tan \psi_2} $$ | High accuracy, grindable teeth | Complex design |
| Circumferential Rotation of Gear | Split Planar Gear Enveloping Screw Gear (Wildhaber Drive) | Relative rotation of split gear halves | $$ \delta = h r_2 $$ | Multiple tooth contact | Inefficient, wear-prone |
| Circumferential Rotation of Gear | Backlash-Free Double Roller Enveloping Screw Gear | Relative rotation of gear halves with rollers | $$ \delta = h r_2 $$ | High efficiency, zero backlash possible | Lower load capacity due to roller shafts |
1. Center Distance Adjustment Principle
This type involves modifying the center distance between the screw and gear in a standard cylindrical screw gear drive. By shifting the screw radially, the effective tooth thickness changes, allowing backlash adjustment. For a screw with axial module \( m_a \) and axial pressure angle \( \alpha \), the normal axial tooth thickness \( s \) at the pitch circle is given by:
$$ s = \frac{\pi m_a}{2} $$
When the screw is moved by a distance \( h \) to reduce the center distance, the new axial tooth thickness \( s’ \) becomes:
$$ s’ = \frac{\pi m_a}{2} + 2h \tan \alpha $$
The backlash compensation \( \delta \) is related to \( h \) as:
$$ \delta = 2h \tan \alpha $$
This method is straightforward and cost-effective, commonly used in machine tool indexing tables. However, it alters the meshing geometry, leading to uneven contact and increased wear. In screw gear applications, such adjustments are often made via shims or eccentric sleeves, but they may not be suitable for high-precision systems due to compromised performance.
2. Axial Movement of the Screw Principle
This category includes drives where the screw is axially displaced to adjust backlash. Two prominent examples are dual-lead cylindrical screw gears and conical screw gears.
Dual-Lead Cylindrical Screw Gear: In this design, the screw has different leads on its two tooth flanks, denoted as \( P_1 \) and \( P_2 \) with \( P_2 > P_1 \). The tooth thickness varies linearly along the axis, so axial movement \( h \) changes the engagement position. The backlash compensation is:
$$ \delta = 2h \frac{P_2 – P_1}{P_1 P_2} $$
This allows precise adjustment without affecting the conjugate mesh, but manufacturing the screw and gear is complex due to the need for special hobs. Screw gear drives of this type are found in precision rotary tables, though they suffer from limited simultaneous tooth contact and reduced load capacity.
Conical Screw Gear (Spiroid Drive): Here, the screw is conical with pressure angles \( \alpha_1 \) and \( \alpha_2 \) on its flanks. Axial displacement \( h \) adjusts backlash according to:
$$ \delta = h \cos \beta (\tan \alpha_1 + \tan \alpha_2) $$
where \( \beta \) is the cone angle. This screw gear design offers multiple tooth engagement, high load capacity, and excellent lubrication, making it suitable for aerospace and servo systems. However, the asymmetric pressure angles can lead to uneven loading in reversible drives.
3. Circumferential Rotation of the Screw Principle
This approach uses a split screw consisting of two halves: a solid screw shaft and a hollow screw. By rotating the hollow screw relative to the fixed shaft under axial preload, backlash is adjusted. For a screw with lead \( P \), the compensation \( \delta \) is:
$$ \delta = \frac{h P}{2\pi} $$
where \( h \) is the rotational displacement. This method, used in segmented screw gear drives from companies like OTT, allows easy adjustment and maintains contact patterns. However, only one half of the screw engages the gear at a time, halving the number of contacting teeth and reducing load capacity. The reliance on clamping sleeves also introduces structural weaknesses.
4. Axial Movement of the Gear Principle
In these drives, the gear is axially moved to adjust backlash, leveraging wedge-shaped teeth. Two variants are discussed: variable tooth thickness planar gear and involute gear enveloping screw gears.
Variable Tooth Thickness Planar Gear Enveloping Screw Gear: The gear has inclined teeth with different flank angles \( \beta_1 \) and \( \beta_2 \), forming a wedge. Axial shift \( h \) compensates backlash as:
$$ \delta = h \tan(|\beta_1 – \beta_2|) $$
This screw gear drive provides high precision and wear compensation, with applications in grinding machine indexes and elevator drives. However, the adjustment is not exact due to non-equivalence of axial and circumferential movements, requiring run-in periods.
Variable Tooth Thickness Involute Gear Enveloping Screw Gear: This design uses a gear with unequal spiral angles \( \psi_1 \) and \( \psi_2 \) on its flanks. The backlash compensation formula is:
$$ \delta = 2h \frac{\tan \psi_1 \tan \psi_2}{\tan \psi_1 + \tan \psi_2} $$
It enables high-accuracy grinding of gear teeth and precise adjustment, making it ideal for heavy-duty precision screw gear systems. The drive maintains multiple tooth contact and allows for wear compensation by shifting the gear axially.
5. Circumferential Rotation of the Gear Principle
This category involves rotating split gear halves relative to each other to adjust backlash.
Split Planar Gear Enveloping Screw Gear (Wildhaber Drive): The gear is split along its mid-plane, and relative rotation \( h \) of the halves changes backlash according to:
$$ \delta = h r_2 $$
where \( r_2 \) is the gear pitch radius. This screw gear drive maintains contact on one side of the mesh but can be inefficient and prone to wear due to simultaneous contact on both flanks.
Backlash-Free Double Roller Enveloping Screw Gear: The gear consists of two halves with rollers as teeth. Relative rotation \( h \) adjusts backlash as:
$$ \delta = h r_2 $$
This design replaces sliding friction with rolling contact, offering high efficiency and the potential for zero backlash. However, the small roller support shafts limit load capacity, making it suitable for motion transmission rather than power-intensive applications.
Mathematical Modeling and Analysis
To deeply understand backlash adjustment in screw gear drives, mathematical models are essential. The general relationship between adjustment displacement and backlash change often involves trigonometric functions of pressure angles, spiral angles, or lead parameters. For instance, in many screw gear designs, the backlash compensation \( \delta \) is proportional to the adjustment \( h \) scaled by a factor derived from tooth geometry. Consider a generic screw gear with axial movement of the screw; the backlash can be expressed as:
$$ \delta = k h $$
where \( k \) is a constant dependent on design parameters. For dual-lead screws, \( k = 2(P_2 – P_1)/(P_1 P_2) \), while for conical screws, \( k = \cos \beta (\tan \alpha_1 + \tan \alpha_2) \). These formulas highlight the precision achievable in screw gear backlash control.
Furthermore, wear compensation over time can be modeled by treating backlash increase as a function of operating hours. If wear rate \( w \) is constant, the required adjustment \( h \) after time \( t \) is:
$$ h = \frac{w t}{k} $$
This emphasizes the importance of adjustable mechanisms in maintaining screw gear performance. In high-precision systems, finite element analysis (FEA) can simulate contact stresses and backlash effects, optimizing screw gear designs for minimal clearance.
Advantages and Disadvantages Summary
Each type of backlash-adjustable screw gear drive offers unique benefits and drawbacks, influencing its suitability for specific applications. The following points generalize these aspects:
- Center Distance Adjustment: Simplest and cheapest, but degrades mesh quality, leading to reduced screw gear life.
- Axial Screw Movement: Provides accurate adjustment without altering conjugate action, yet manufacturing complexities and limited load capacity are issues for screw gear drives.
- Circumferential Screw Rotation: Facilitates easy assembly and adjustment, but load capacity is compromised due to split screw design in screw gear systems.
- Axial Gear Movement: Enables high precision and effective wear compensation, ideal for heavy-duty screw gear applications, though some designs require run-in.
- Circumferential Gear Rotation: Allows zero backlash potential and high efficiency, but structural weaknesses may limit use in high-load screw gear scenarios.
The choice of screw gear type depends on factors like required accuracy, load, speed, and maintenance capabilities. For instance, in CNC machine tools, dual-lead screw gears are common for their precision, while in aerospace, conical screw gears are preferred for their robustness.
Future Trends in Backlash-Adjustable Screw Gear Drives
As industrial demands evolve, backlash-adjustable screw gear drives are expected to advance in two key directions: precision heavy-duty types and high-efficiency types.
Precision Heavy-Duty Screw Gear Drives: Applications such as high-speed gear hobbing machines, ship stabilization systems, and military targeting units require screw gear drives that combine high load capacity with minimal backlash. Drives based on axial movement of the gear, like variable tooth thickness involute gear enveloping screw gears, are promising. They allow multiple tooth contact, precise grinding, and wear compensation, making them suitable for these demanding roles. Future research may focus on improving material science to enhance wear resistance and developing advanced manufacturing techniques for complex screw gear geometries.
High-Efficiency Screw Gear Drives: In aerospace and energy-sensitive applications, efficiency is critical. Backlash-free double roller enveloping screw gear drives offer high efficiency by replacing sliding friction with rolling contact. Future developments could involve optimizing roller bearing designs to increase load capacity while maintaining adjustability. Additionally, integrating smart sensors for real-time backlash monitoring and automatic adjustment in screw gear systems could revolutionize maintenance and performance.
Overall, the trend is toward screw gear drives that are not only adjustable but also intelligent, durable, and tailored to specific operational environments. The continued use of screw gear mechanisms in robotics and automation will drive innovation in backlash control technologies.
Conclusion
Backlash-adjustable screw gear drives are essential components in modern precision mechanical systems, offering solutions to mitigate clearance-related issues. This review has classified these drives into five categories based on adjustment principles, detailing their mathematical relationships, advantages, and disadvantages. From simple center distance adjustments to complex enveloping designs, each type serves distinct applications, with screw gear technology continuously evolving to meet higher standards of accuracy and efficiency. The future points toward heavy-duty and high-efficiency screw gear drives, leveraging advancements in materials and manufacturing. As a fundamental element in transmission engineering, the screw gear remains at the forefront of innovation, ensuring reliable performance in increasingly demanding contexts.
