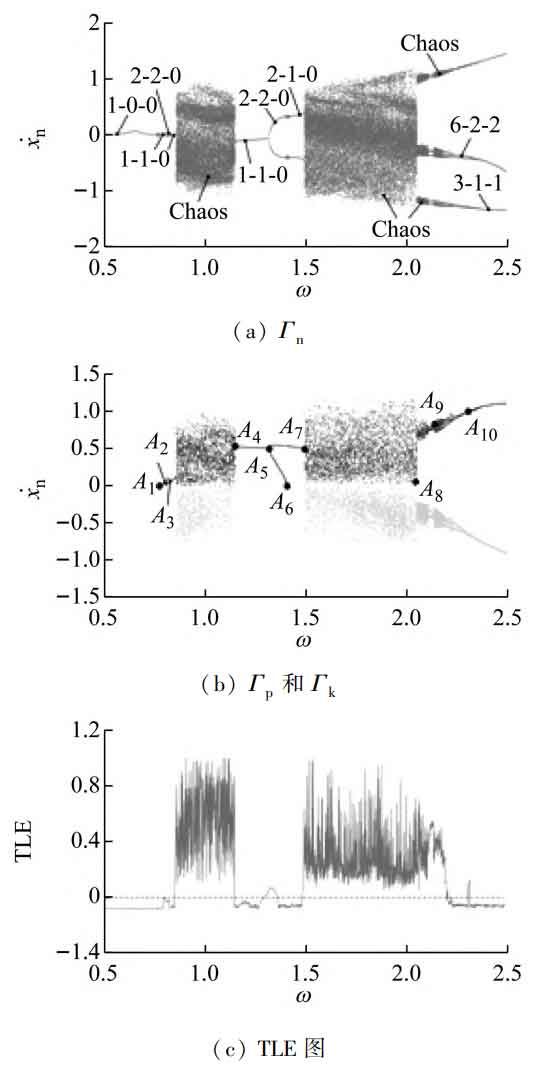
Take dimensionless parameters ω = 0. 73、F = 0. 1、 ζ = 0.05, the values of other parameters are the same as 3.1, and the comprehensive transmission error can be obtained ε The bifurcation diagram and TLE diagram of three kinds of Poincar é cross sections are shown in Figure 1.
When ε When it is small (on the left side of point B1), the system is in stable 1 ⁃ 0 ⁃ 0 motion, and only the tooth surface of straight bevel gear mesh. ε When increasing to point B1, the phase track of the system is tangent to xn=D, and the 1 ⁃ 0 ⁃ 0 motion transits to 1 ⁃ 1 ⁃ 0 motion through the friction and cutting bifurcation, and the gear tooth disengagement occurs in the system. Due to the small vibration amplitude, the effect of single and double teeth alternate meshing of the system is obvious, and the phase track of the system fluctuates. At this time, the phase diagram and time history diagram are shown in Figure 2 (a) and 2 (b). ε When it is increased to B2, the system changes from 1 ⁃ 1 ⁃ 0 motion to 2 ⁃ 2 ⁃ 0 motion through doubling bifurcation, and there are two operating states in the system: straight bevel gear tooth surface meshing and gear tooth meshing.
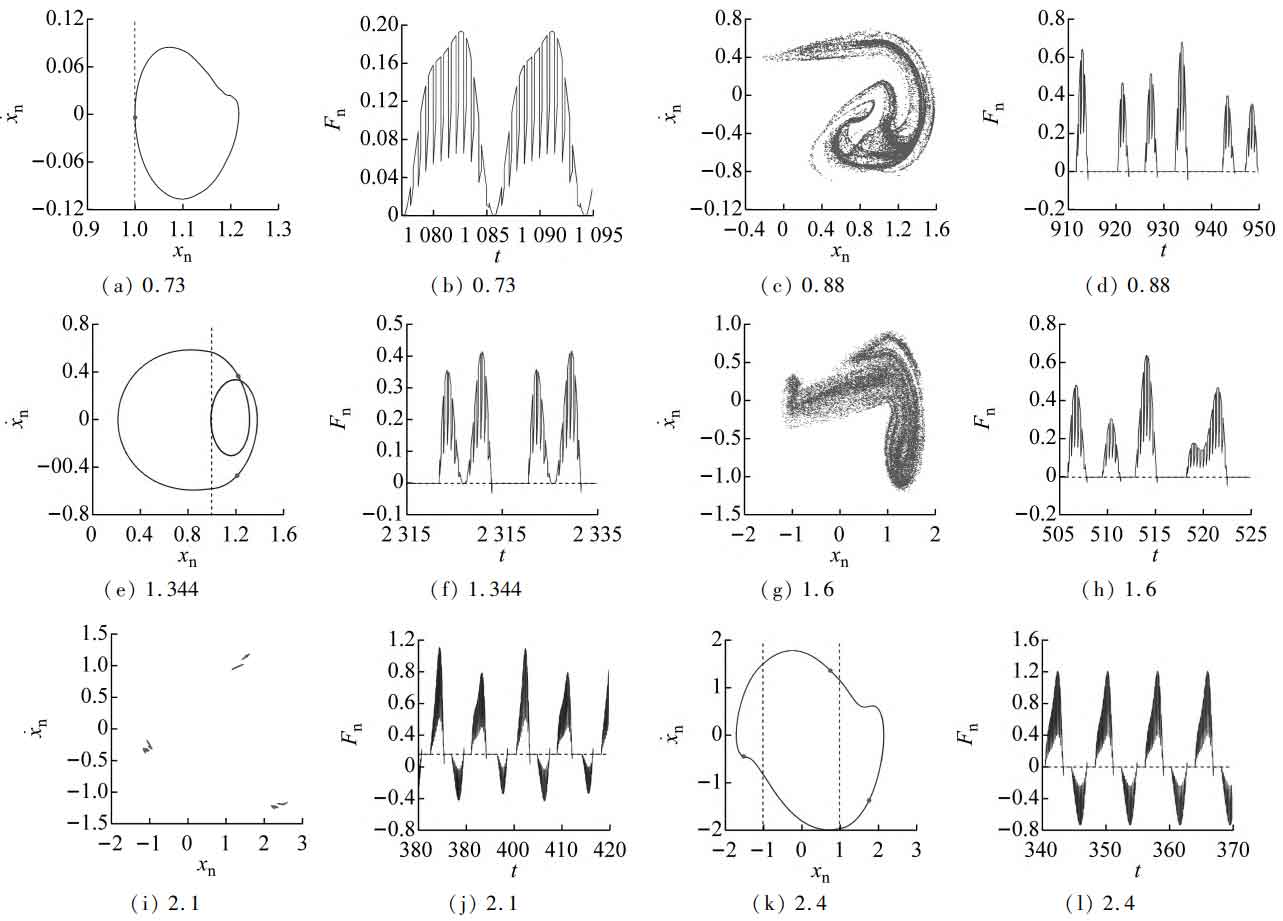
With ε When it is increased to B3, the system will be degraded from 2 ⁃ 2 ⁃ 0 motion to 2 ⁃ 1 ⁃ 0 motion after friction and the half value of the system phase path passing through the tooth side gap will be reduced from the previous two times to one time. At this time, the phase diagram and time history diagram are shown in Figure 2 (c) and 2 (d). When ε When it is increased to B4, the system changes from 2 ⁃ 1 ⁃ 0 motion to chaotic motion through saddle node bifurcation. In the chaotic region, the system has three operating states: straight bevel gear tooth surface meshing, gear tooth meshing and tooth back contact. At this time, the phase diagram and time history diagram are shown in Figure 2 (e) and 2 (f).
It can be seen that with the increase of the amplitude of the fluctuation of the comprehensive transmission error, the gear tooth disengagement and tooth back contact state gradually appear in the system, and its multi-state meshing behavior and motion characteristics become complex, and the stability deteriorates. Therefore, the manufacturing accuracy of straight bevel gear transmission system should be improved and the comprehensive transmission error should be reduced to improve its motion stability.
