In the field of automotive and mechanical engineering, hypoid gears have become indispensable components due to their superior performance characteristics. As an engineer involved in gear manufacturing, I have witnessed the growing adoption of hypoid gears in vehicles, transport machinery, and construction equipment. Their advantages are well-documented: enhanced strength of the pinion, larger overlap ratio, uniform磨合 of relative sliding surfaces, and the ability to lower the vehicle’s center of gravity. However, the design and manufacturing processes for hypoid gears are notoriously complex, requiring extensive calculations for geometric parameters, cutting tool settings, and machine adjustments. Traditional methods rely on specialized software, such as those from Gleason Company, but these are often expensive and inaccessible for many small to medium-sized enterprises. In response, our team developed an in-house computer program to streamline the design and production of hypoid gears, making it feasible for factories with limited resources to produce high-quality gears efficiently.
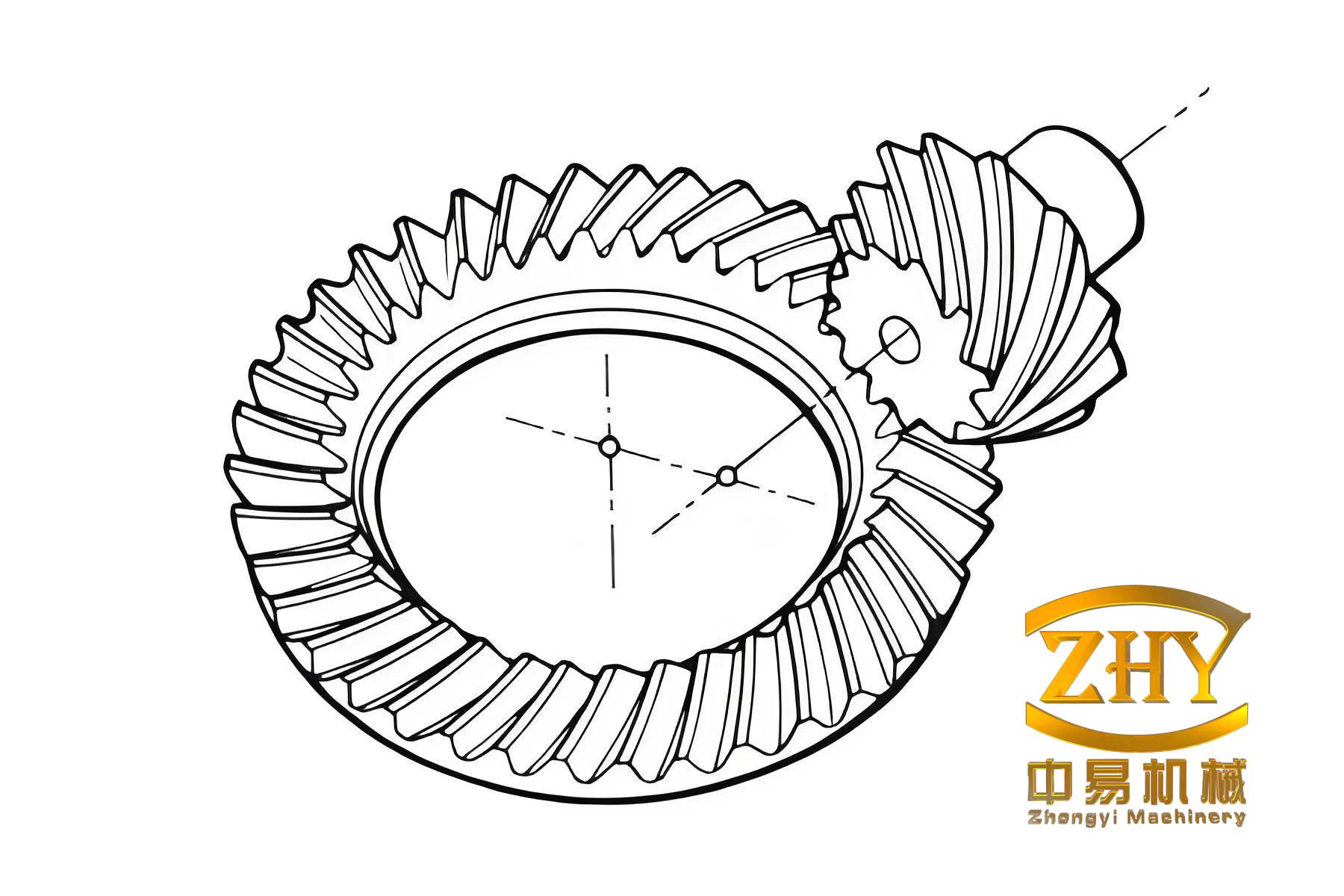
The impetus for creating this program stemmed from practical challenges. While advanced software solutions exist, they often require high-end computers or cloud-based systems, leading to delays and high costs. For instance, sending drawings to remote centers for computation is not only time-consuming but also financially burdensome. Our goal was to develop a program that could run on low-cost microcomputers, such as the Apple II or IBM PC, without sacrificing accuracy. This initiative has empowered our factory to produce hypoid gears for various applications, including rear axles for trucks and large gears for construction machinery, with notable success in reducing noise and improving durability.
Our hypoid gear program boasts several distinctive features that set it apart from commercial alternatives. First, it is optimized for low-specification microcomputers, ensuring accessibility even for workshops with basic hardware. Second, the user interface is intuitive, allowing engineers who may not be experts in hypoid gear theory to quickly apply it to production tasks. Third, it supports small and medium-sized factories in developing new hypoid gear products reliably. Fourth, the initial calculation results typically yield satisfactory contact patterns, and minor adjustments based on proportional corrections can achieve optimal performance. Fifth, it reduces the need for specialized cutting tool heads, enabling the use of existing tool inventories, which cuts costs and increases flexibility. These features have been validated through real-world production, such as for the Dongfeng-12 vehicle rear axle hypoid gears, which received industry recognition for quality.
| Feature | Description | Benefit |
|---|---|---|
| Low Hardware Requirements | Runs on microcomputers like Apple II or IBM PC | Cost-effective and accessible |
| Ease of Use | Intuitive interface for non-experts | Reduces training time |
| Reliability for SMEs | Supports new product development | Enhances innovation capacity |
| Initial Contact Pattern Quality | Produces good contact zones from first calculation | Minimizes trial-and-error |
| Tool Head Compatibility | Utilizes existing tool inventories | Lowers production costs |
The program is structured into multiple subroutines, each handling specific aspects of hypoid gear design and manufacturing. Overall, it comprises 15 subroutines that work in tandem to compute geometric parameters, cutting tool configurations, and machine adjustment settings. The workflow begins with inputting basic gear data, proceeds through iterative calculations for optimal parameters, and concludes with detailed output reports. This modular approach ensures flexibility and accuracy, as each subroutine focuses on a well-defined task, such as calculating the spiral angle or determining the pressure angle for cutting tools. The core algorithms are based on established hypoid gear theory, particularly the Gleason “G-Format” cutting principles, but adapted for computational efficiency and practicality.
To initiate the program, users must provide a set of input parameters that define the hypoid gear pair. These parameters are critical for ensuring the accuracy of subsequent calculations. Below is a comprehensive table listing all required inputs, along with their descriptions and typical units. This data serves as the foundation for the entire design process, influencing everything from tooth geometry to machine setup.
| Parameter | Symbol | Description | Unit |
|---|---|---|---|
| Gear Hand | – | Rotation direction of gears (left or right) | – |
| Number of Teeth on Gear | \(N_g\) | Tooth count for the larger gear | – |
| Number of Teeth on Pinion | \(N_p\) | Tooth count for the smaller gear | – |
| Face Width of Gear | \(F_g\) | Width of the gear tooth along the pitch cone | mm |
| Offset Distance | \(E\) | Distance between axes of gear and pinion | mm |
| Pitch Diameter of Gear | \(D_g\) | Diameter at the pitch circle of the gear | mm |
| Nominal Diameter of Cutter | \(D_c\) | Public diameter of the cutting tool | mm |
| Spiral Angle of Pinion | \(\beta_p\) | Angle of pinion tooth spiral relative to axis | degrees |
| Tooth Height Coefficient | \(k_h\) | Factor for determining tooth height | – |
| Mean Pressure Angle | \(\alpha_m\) | Average pressure angle of the gear pair | degrees |
| Addendum Coefficient of Gear | \(k_{a,g}\) | Factor for gear addendum height | – |
| Dedendum Coefficient of Gear | \(k_{d,g}\) | Factor for gear dedendum height | – |
| Minimum Backlash | \(B_{min}\) | Smallest allowable clearance between teeth | mm |
| Maximum Backlash | \(B_{max}\) | Largest allowable clearance between teeth | mm |
| Machine Constant for Gear Cutting | \(M_g\) | Constant specific to the gear cutting machine | – |
| Machine Constant for Pinion Cutting | \(M_p\) | Constant specific to the pinion cutting machine | – |
| Mounting Distance of Gear | \(A_g\) | Distance from gear reference point to mounting surface | mm |
| Mounting Distance of Pinion | \(A_p\) | Distance from pinion reference point to mounting surface | mm |
Once the input data is provided, the program executes a series of calculations to determine the hypoid gear geometry. These computations involve iterative methods to achieve convergence for parameters such as the spiral angle and pressure angles. For example, the root line spiral angle of the gear, denoted as \(\beta_{g,root}\), is derived from the offset and pitch geometry. The formula for this angle can be expressed as:
$$ \beta_{g,root} = \arctan\left(\frac{E}{R_g}\right) + \Delta \beta $$
where \(R_g\) is the pitch radius of the gear, and \(\Delta \beta\) is a correction factor based on tooth geometry. Similarly, the limiting pressure angle for the pinion root line, \(\alpha_{p,limit}\), is calculated to ensure proper mesh and avoid undercutting. This angle is critical for defining the tooth profile and is given by:
$$ \alpha_{p,limit} = \alpha_m – \frac{\theta}{2} $$
Here, \(\theta\) represents the angular offset due to the hypoid configuration. These formulas are embedded in the program’s subroutines, which perform checks to ensure that calculated values fall within acceptable ranges. For instance, the program verifies that the face cone and root cone of both gear and pinion do not exceed the crossover point, which could lead to manufacturing defects.
The program also includes a sophisticated module for cutting tool calculation, which is essential for producing accurate hypoid gears. This module operates in three distinct modes, allowing users to select the most suitable approach based on available tooling. Mode 1 automatically selects cutter pressure angles based on the mean pressure angle, subject to constraints. For the gear convex side, the cutter pressure angle \(\alpha_{c,g}\) must satisfy:
$$ \alpha_{c,g} = \alpha_m \pm \delta_1 $$
where \(\delta_1\) is a tolerance, typically within 1 degree. For the pinion concave side, the condition is:
$$ \alpha_{c,p} = \alpha_m \pm \delta_2 $$
with \(\delta_2\) also around 1 degree. Mode 2 allows manual input of up to three sets of existing tool head numbers for both gear convex and pinion concave sides, with the program validating them against the same constraints. Mode 3 utilizes a built-in database of common tool heads, enabling automatic selection via a user-controlled switch. This flexibility ensures that factories can leverage their current tool inventories without compromising on precision.
After determining the cutter parameters, the program computes the cutter offset and forming diameter. The forming diameter, \(D_f\), is crucial for defining the tooth surface and is calculated using the formula:
$$ D_f = D_c + 2 \cdot \Delta O $$
where \(\Delta O\) is the cutter offset derived from the gear geometry. The program then displays a range of acceptable forming diameters for the pinion finishing cutter, allowing users to choose a value based on available tooling. This interactive step bridges the gap between theoretical design and practical manufacturing constraints.
With all geometric and tool parameters established, the program proceeds to machine adjustment calculations. These adjustments are vital for setting up the cutting machines to produce the hypoid gears accurately. For the gear, separate calculations are performed for roughing and finishing cuts, accounting for factors like machine constants and mounting distances. The pinion adjustments follow a similar process, with additional iterations to optimize the contact pattern. The underlying equations often involve trigonometric relationships, such as:
$$ X = M_g \cdot \sin(\phi) + C $$
where \(X\) is a machine setting, \(\phi\) is an angle derived from the gear geometry, and \(C\) is a constant. These calculations ensure that the cutting tools are positioned correctly relative to the workpiece, minimizing errors and enhancing the quality of the final hypoid gear pair.
The output of the program is comprehensive, presented in a tabular format that summarizes approximately 100 different process parameters. This includes geometric data for both gear and pinion, cutter specifications for roughing and finishing, and machine adjustment settings. Below is a condensed table illustrating some key output categories:
| Category | Parameters Included | Example Values |
|---|---|---|
| Gear Geometry | Pitch diameter, spiral angle, addendum, dedendum | \(D_g = 200\,mm\), \(\beta_g = 30^\circ\) |
| Pinion Geometry | Root line pressure angle, face cone distance | \(\alpha_{p,limit} = 18^\circ\), \(L_p = 50\,mm\) |
| Cutter Parameters | Pressure angles, forming diameter, offset | \(\alpha_{c,g} = 20^\circ\), \(D_f = 150\,mm\) |
| Gear Machine Adjustments | Machine constants, tilt angles, sliding bases | \(M_g = 1.5\), tilt = 5° |
| Pinion Machine Adjustments | Setting angles, offsets, rotational positions | Offset = 2.3 mm, rotation = 120° |
This detailed output enables engineers to directly apply the results to production lines, reducing setup time and improving consistency. In our factory, we have used this program to manufacture hypoid gears for various vehicles, including Isuzu truck rear axles and Mitsubishi construction machinery. The gears produced exhibit excellent contact patterns and low noise levels, demonstrating the program’s effectiveness. For instance, in one project, we achieved a contact zone centered on the tooth flank with minimal bias, which is critical for load distribution and longevity.
Despite its successes, the program has limitations. Notably, it does not include tooth contact analysis (TCA), which simulates the meshing behavior under load to predict performance and noise characteristics. TCA is a complex but valuable tool for optimizing hypoid gear designs, and its absence means that some fine-tuning may require physical testing. However, our program compensates by providing robust initial calculations that often yield acceptable results, and we have developed empirical correction factors based on production experience. For example, we use proportional adjustments to shift the contact pattern if needed, guided by the formula:
$$ \Delta C = k \cdot \frac{\Delta \beta}{\beta_{nom}} $$
where \(\Delta C\) is the correction to a machine setting, \(k\) is a proportionality constant, and \(\beta_{nom}\) is the nominal spiral angle. This pragmatic approach has allowed us to achieve satisfactory outcomes even without advanced simulation capabilities.
Looking ahead, we aim to enhance the program by integrating TCA functionalities and adapting it for modern programming environments. The rise of CNC machines and digital manufacturing underscores the need for more sophisticated software tools. By collaborating with academic experts and leveraging open-source resources, we hope to develop a version that includes real-time contact analysis, making it even more powerful for hypoid gear production. Additionally, we plan to expand the tool database to include a wider range of cutter profiles, further increasing flexibility.
In conclusion, the development of this computer program has revolutionized our approach to hypoid gear manufacturing. By combining theoretical principles with practical adaptability, it addresses the core challenges faced by small and medium-sized enterprises. The program’s ability to run on low-cost hardware, its user-friendly design, and its compatibility with existing tooling make it a valuable asset for anyone involved in gear production. As hypoid gears continue to gain prominence in various industries, tools like this will play a crucial role in democratizing access to high-quality gear design and manufacturing. Through continuous improvement and collaboration, we believe that such programs can contribute significantly to advancing mechanical engineering practices worldwide.
The mathematical rigor embedded in the program ensures that every hypoid gear produced meets stringent quality standards. For instance, the calculation of the offset angle in the pinion rotation plane, denoted as \(\gamma\), is derived from the gear geometry and influences the cutting process. This angle is computed as:
$$ \gamma = \arcsin\left(\frac{E}{L_p}\right) $$
where \(L_p\) is the pinion reference distance. Such formulas are integral to achieving precise tooth profiles. Moreover, the program iteratively solves for optimal parameters, using convergence criteria to ensure accuracy. For example, the spiral angle adjustment continues until the difference between iterations is less than a tolerance \(\epsilon\), typically set to 0.001 degrees. This attention to detail underscores the program’s reliability.
To further illustrate the program’s capabilities, consider the calculation of the tooth thickness and space width. These dimensions are critical for ensuring proper meshing and backlash control. The program uses the following relationships, based on the hypoid gear geometry:
$$ t_g = \frac{\pi \cdot D_g}{N_g} – s_g $$
$$ s_p = \frac{\pi \cdot D_p}{N_p} – t_p $$
where \(t_g\) and \(t_p\) are the tooth thicknesses of the gear and pinion, respectively, and \(s_g\) and \(s_p\) are the space widths. The program adjusts these values based on the input backlash requirements, ensuring that the final gear pair operates smoothly without excessive play or interference.
In terms of manufacturing, the program’s output directly guides the setup of cutting machines. For the gear roughing process, parameters such as the cutter tilt angle and radial distance are calculated to remove material efficiently while preserving the tooth form. For finishing, more precise adjustments are made to achieve the final surface quality. The pinion cutting process is similarly detailed, with separate routines for concave and convex sides to account for their distinct geometries. This level of granularity is essential for producing hypoid gears that meet performance specifications.
Overall, the program represents a significant step forward in making hypoid gear technology accessible. By automating complex calculations and providing clear outputs, it reduces the barrier to entry for many manufacturers. As we continue to refine and expand its features, we anticipate that it will become an even more indispensable tool in the gear industry, fostering innovation and improving product quality across the board.
