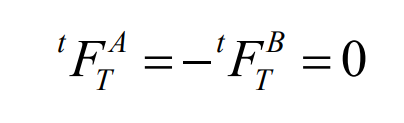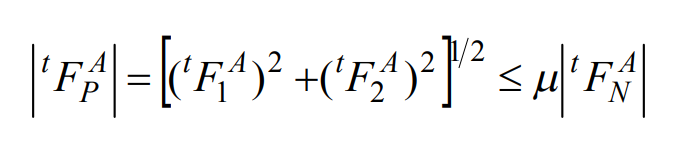The finite element analysis method of spiral bevel gear has gradually developed into a widely used numerical analysis method, and has achieved good results in various disciplines and engineering fields. The finite element analysis method of spiral bevel gear can solve the mechanical problems in a variety of complex engineering structures. The essence of the finite element analysis method of spiral bevel gear is to transform the continuous system composed of countless degrees of freedom into a unit assembly composed of finite degrees of freedom, and transform the problem to be solved into a structural problem suitable for numerical method. This process is idealized. This method can deal with complex working conditions and boundary conditions that cannot be completed by traditional methods.
Finite element software is the carrier of integrating finite element formula and technology. In order to use the finite element software to analyze and calculate the actual problems and get the correct results, it is necessary to understand the basic solution equations of finite element analysis. The basic equation of finite element solution for loaded contact analysis is obtained by adding the boundary conditions corresponding to the contact conditions on the basis of the basic equation of finite element solution. Suppose that the two spiral bevel gears are in contact for a and B, and t Ω is the volume of the two spiral bevel gears at time t, t Γ D is the boundary condition imposed by displacement, t Γ F is the boundary condition applied by the load, then the basic equation of the loaded contact finite element solution is:
(1) Equilibrium equation
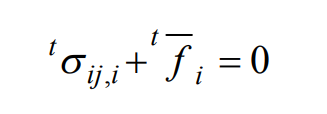
(2) Geometric equation
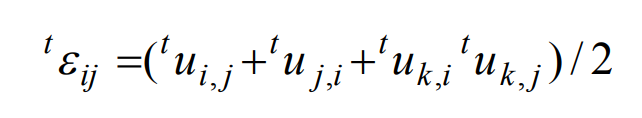
(3) Constitutive equation
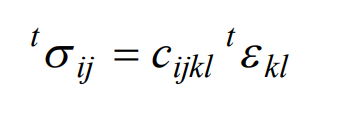
(4) Initial conditions
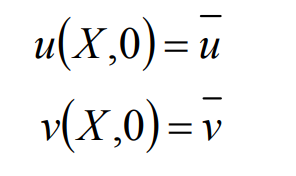
(5) Displacement boundary condition
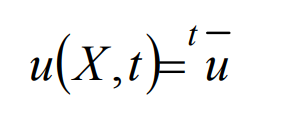
(6) Force boundary condition
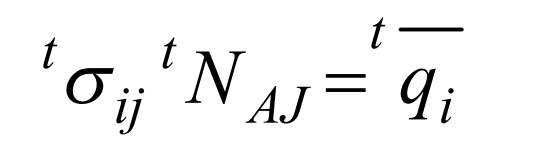
(7) Normal contact condition
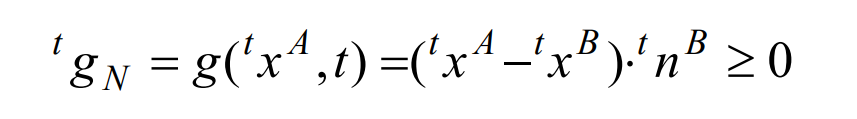
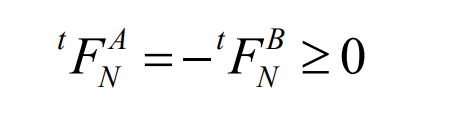
(8) Tangential contact condition