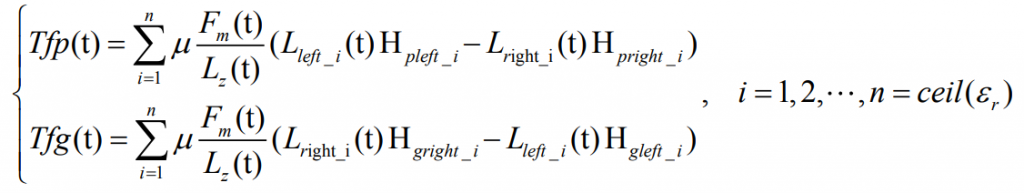According to Newton’s second law of motion and D’Alembert’s principle, an 8-DOF torsional vibration and translational vibration coupling dynamic model of helical gear system excited by helical gear modification and friction is established, as shown in Figure. Driving wheel P and driven wheel g have 4 degrees of freedom respectively. Since the specific vibration forms of transmission shaft, etc. are not considered, the equivalent values of support stiffness and damping of transmission shaft, bearing and box can be KPX, KPY, KPZ, kgx, kGy, KGZ and CPX, CPY, CPZ, cgx, cGy and CGZ. In Figure 4.2, the y-axis is in the direction of the meshing line of the helical gear, and IP and Ig are the moment of inertia of the driving wheel and the driven wheel respectively; MP and Mg are the masses of driving wheel and driven wheel respectively; TP and TG are the input and output torques of the driving wheel and the driven wheel respectively; θ P and θ G is the angular displacement of driving wheel and driven wheel respectively; Km and MC are the comprehensive meshing stiffness and tooth meshing damping of helical gear system respectively; FFP and FFG are the friction force on the driving wheel and the driven wheel respectively; RBP and RBG are the base circle radii of driving wheel and driven wheel respectively.
It can be seen that considering the tooth surface friction, which is perpendicular to the meshing line direction (x-axis direction), the dynamic model is a three-dimensional spatial vibration system, including 2 rotational degrees of freedom and 6 translational degrees of freedom.
Two degrees of freedom torsional vibration equations are established as follows:
Of which:
The translational vibration equations of 6 degrees of freedom are established as follows:
Of which:
The dynamic meshing force of helical gear is the sum of elastic meshing force FK and viscous meshing force FC between meshing teeth:
Elastic meshing force between meshing teeth of helical gear:
Viscous meshing force between meshing teeth of helical gear:
The dynamic meshing force of helical gear in tangential (Y-axis direction) and axial (Z-axis direction) is:
The dynamic meshing damping of helical gear is:
The friction force of driving wheel and driven wheel of helical gear system is the same and the direction is opposite. Its calculation expression is:
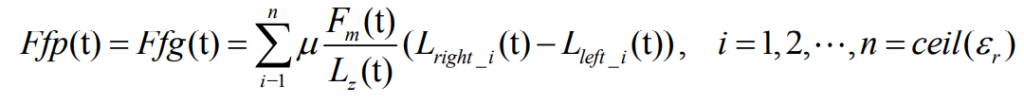
The calculation expression of friction torque of driving wheel and driven wheel of helical gear system is:
Dynamic transmission error is an important parameter characterizing the dynamic response characteristics of helical gear meshing system. In order to analyze the influence of modification and friction excitation on the dynamic transmission error of helical gear meshing system, the calculation formula of dynamic transmission error of helical gear system along the meshing line is as follows: