The figure shows the maximum value Max (u) of dimensionless vibration displacement u and the minimum value Min (v) of vibration displacement v as a function of the helical gear load ratio λ The variation trend of load value f1 indicates that:
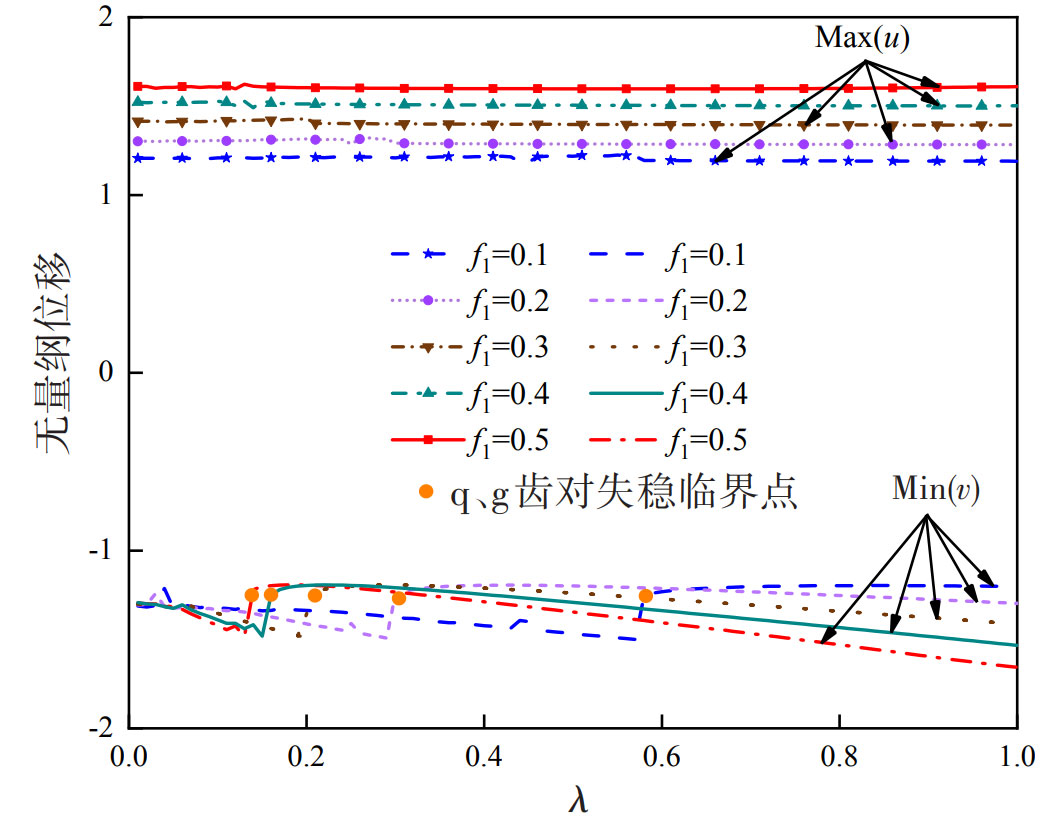
(1) The change in load ratio of helical gears has a relatively small impact on the p and g tooth pairs at the high load input end; For the q and g tooth pairs at the low load input end, as the load ratio of the helical gear increases λ With the improvement of Min (v), there will be a stability mutation, which corresponds to the previous analysis, indicating that the system has a transition between chaotic and periodic motion states at this critical point of instability.
(2) As the load f1 of the helical gear increases, the Max (u) at the high load input end also increases; For the low load input end, as the load f1 of the helical gear increases, the critical point of instability is directed towards the load ratio λ Development in the direction of reduction. When the load ratio of the helical gear is λ< At 0.13, the system is in chaotic motion under all load conditions f1, and as the load f1 increases, | Min (v) | gradually increases; When 0.13< λ< At 0.57, the trend of | Min (v) | is related to the timing when different loads f1 pass through the critical point of instability; When the load ratio of the helical gear is λ> At 0.57, the system is in periodic motion under all helical gear load f1 conditions. At this time, as the helical gear load f1 increases, | Min (v) | also gradually increases.
