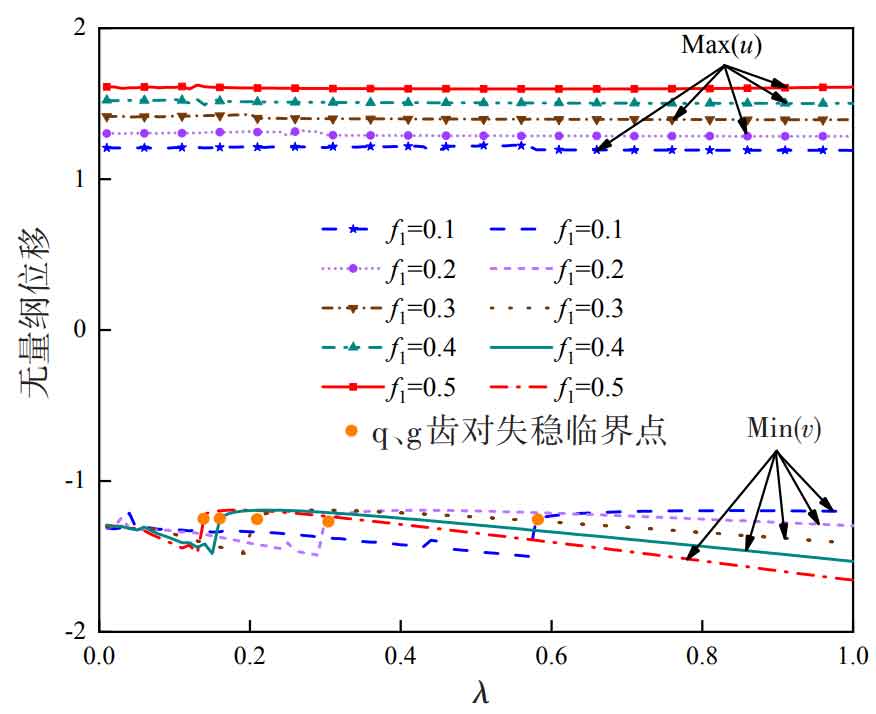
As shown in the figure, the maximum value of dimensionless vibration displacement u Max (u) and the minimum value of vibration displacement v Min (v) vary with load ratio λ And load value f1, indicating:
(1) The change of load ratio of helical gear has little effect on the p and g tooth pairs at the high load input end; For the q and g tooth pairs at the low load input end, the load ratio λ There will be a sudden change of stability in Min (v), which corresponds to the above analysis, indicating that there is a jump of chaotic motion state and periodic motion state of the system at the critical point of instability.
(2) With the increase of helical gear load f1, the Max (u) at the high load input end increases; For the low load input end, with the increase of load f1, the critical point of instability is the load ratio λ Development in the direction of reduction.
When the load ratio of helical gear λ< At 0.13, the system is in chaotic motion under all load f1 conditions. At this time, | Min (v) | gradually increases with the increase of load f1; When 0.13< λ< At 0.57, the change trend of | Min (v) | is related to the time when different loads f1 pass the critical point of instability; When the load ratio of helical gear λ> At 0.57, the system is in periodic motion under all load f1 conditions. At this time, with the increase of load f1, | Min (v) | also increases gradually.
