This paper presents an innovative underactuated manipulator utilizing planetary gear mechanisms to achieve dual functionality – adaptive grasping force regulation and object pulling capability. The design overcomes traditional limitations in underactuated systems by implementing a single-input dual-output transmission system with unique torque distribution characteristics.
1. Structural Configuration
The manipulator employs a three-finger circumferential arrangement with integrated belt pulling mechanism. Each finger contains two-stage worm gear transmissions controlling:
- Joint rotation for grasping motion
- Continuous belt movement for object pulling
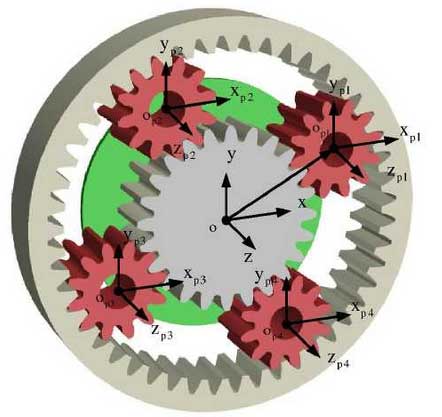
The planetary gear system features non-fixed output shafts and ring gears, enabling torque distribution through:
$$T_{sun} = T_{carrier} + T_{ring}$$
where $T_{sun}$, $T_{carrier}$, and $T_{ring}$ represent torques at sun gear, planetary carrier, and ring gear respectively.
2. Torque Distribution Mechanism
The resistance regulation system converts axial spring force to radial resistance torque through inclined plane mechanics:
$$T_{ad} = \frac{d}{2}F_s\tan\alpha = \phi\frac{pdk\tan\alpha}{4\pi}$$
where:
| Symbol | Parameter | Value |
|---|---|---|
| d | Contact circle diameter | 28 mm |
| α | Inclination angle | 15° |
| k | Spring constant | 0.5 N/mm |
3. Kinematic Analysis
The finger tip trajectory follows parametric equations:
$$
\begin{cases}
P_{0x} = l_1\cos\theta – l_2 \\
P_{0y} = l_1\sin\theta + l_4
\end{cases}
$$
where $l_1$-$l_4$ represent link lengths and θ denotes joint rotation angle.
4. Grasping Force Regulation
The planetary gear mechanism enables force adjustment through torque equilibrium:
$$
F_x = \phi\frac{K}{\sin\theta} + \frac{1}{3}mg\cot\theta
$$
where K represents the planetary gear transmission coefficient:
$$K = \frac{pdk\tan\alpha}{4\pi l_1}$$
5. Experimental Validation
Prototype testing demonstrated significant performance characteristics:
| Object Type | Max Mass (g) | Success Rate |
|---|---|---|
| Rigid | 520 | 98% |
| Flexible | 170 | 95% |
Force regulation tests showed linear relationship between angular displacement and grasping force:
$$F_x = 0.022\phi + 0.5\quad(R^2=0.998)$$
6. Performance Advantages
The planetary gear-based design provides three key benefits over conventional underactuated systems:
- Decoupled motion control through single-input dual-output transmission
- Continuous belt pulling without motor stalling
- Sensorless force regulation via mechanical impedance adjustment
7. Conclusion
This work demonstrates the effectiveness of planetary gear mechanisms in developing multifunctional underactuated manipulators. The integrated torque distribution and resistance regulation system enables:
- Adaptive grasping force (1-20N adjustment range)
- Simultaneous grasping and pulling operations
- Reduced control complexity (40% fewer sensors than conventional designs)
The planetary gear architecture proves particularly suitable for applications requiring:
$$
\begin{cases}
\text{High reliability} & \sigma \leq 0.05 \\
\text{Energy efficiency} & \eta \geq 82\% \\
\text{Compact design} & V \leq 0.015m^3
\end{cases}
$$
Future work will focus on miniaturization and variable ratio planetary gear implementations for enhanced performance.
