In my extensive experience designing cutting tools for precision gear systems, I have often encountered the unique challenges posed by small module involute strain wave gears. These gears, with module values of 1 mm or less, are critical components in aerospace, aviation, and high-precision instrumentation due to their compact size, high torque capacity, and smooth motion transmission. The core of a strain wave gear system, often referred to as a harmonic drive, consists of three primary elements: a rigid circular spline (often called the “ring gear” or “steel wheel”), a flexible spline (the “flexspline”), and a wave generator. The operating principle relies on the elastic deformation of the flexspline, induced by the wave generator, to create a moving wave that meshes progressively with the teeth of the rigid circular spline, enabling high-ratio speed reduction in a minimal space.
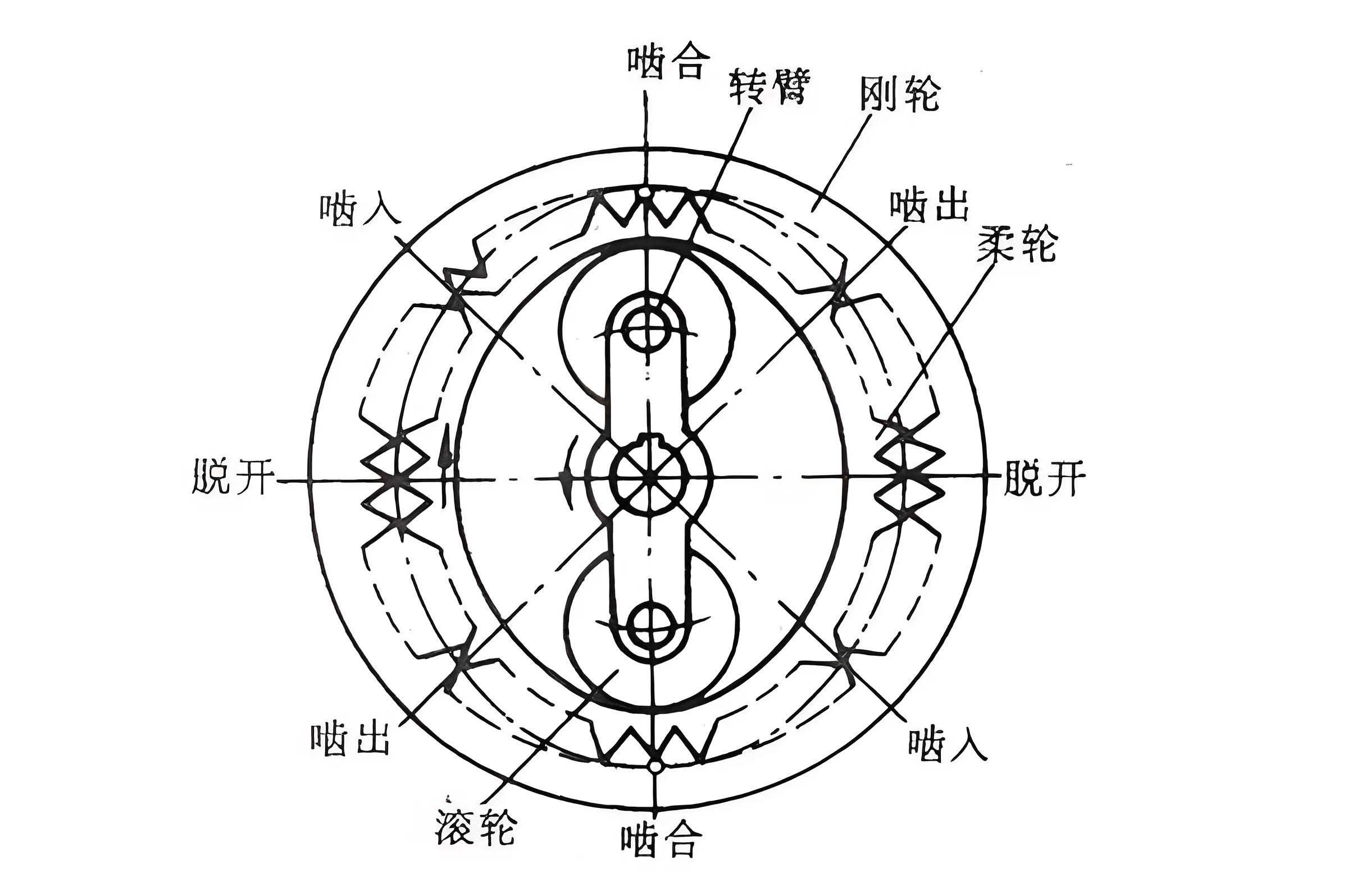
The manufacturing of the internal teeth on the rigid circular spline of a strain wave gear is typically accomplished using a shaper cutter. A shaper cutter resembles a gear but incorporates cutting angles—rake and relief angles—on its teeth. It operates on the generating principle, where its cutting edges emulate a mating gear to produce the desired tooth profile on the workpiece. While a single shaper cutter can generate gears of the same module and pressure angle but with different numbers of teeth, and can handle both standard and profile-shifted gears, the design process becomes exceptionally complex when dealing with the internal splines of strain wave gears. These gears invariably employ significant positive profile shift (modification) to avoid undercutting of the flexible spline and to optimize the contact pattern and load distribution. This large positive shift coefficient often results in a peculiar geometric condition: the minor diameter (tip diameter) of the internal gear becomes larger than its pitch diameter. This condition renders conventional shaper cutter design methods inapplicable, necessitating a more sophisticated approach based on the concept of variable module and variable pressure angle. This article details my methodology for designing shaper cutters under these constraints, a process vital for producing reliable and efficient strain wave gear systems.
To fully appreciate the design challenge, a thorough analysis of the positively shifted internal spline is essential. The fundamental parameters of a standard involute gear include the module \(m\), the pressure angle at the pitch circle \(\alpha\), the number of teeth \(z\), the addendum \(h_a\), and the dedendum \(h_f\). The pitch diameter \(d_f\) is defined by the well-known relation:
$$ d_f = m \cdot z $$
For an internal gear, the minor diameter \(d_a\) is the tip diameter, and the major diameter \(d_i\) is the root diameter. The circular pitch \(P\) at any diameter \(d\) is given by \(P = \pi d / z\). At the pitch circle, it simplifies to \(P = \pi m\). In a standard, non-shifted gear (\(\xi = 0\)), the tooth thickness \(S\) and the space width \(W\) on the pitch circle are equal:
$$ S = W = \frac{P}{2} = \frac{\pi m}{2} $$
The addendum and dedendum for an internal gear are calculated as:
$$ h_a = \frac{d_f – d_a}{2} \quad \text{(for internal gears, } d_a < d_f \text{)} $$
$$ h_f = \frac{d_i – d_f}{2} $$
Profile shifting, or modification, is employed to prevent undercutting in pinions with low tooth numbers and to adjust center distances. It involves offsetting the basic rack tool relative to the gear blank. A positive shift (\(\xi > 0\)) moves the tool away from the gear center, resulting in a gear that uses a portion of the involute curve with a larger radius of curvature. The magnitude of the shift is \(X = m \cdot \xi\). This shift alters the tooth thickness on the pitch circle. For a profile-shifted gear, the pitch circle tooth thickness is:
$$ S = \frac{\pi m}{2} \pm 2m \xi \tan \alpha $$
where the plus sign applies to external gears and the minus sign applies to internal gears. Consequently, the addendum and dedendum are also modified. For a positively shifted internal gear, the entire tooth profile effectively shifts radially outward. The minor diameter \(d_a\) increases, and the major diameter \(d_i\) also increases. When the positive shift coefficient \(\xi\) is sufficiently large, a critical condition arises where the minor diameter \(d_a\) exceeds the pitch diameter \(d_f\). This implies the pitch circle lies inside the tooth tip, a situation geometrically impossible for a standard shaper cutter designed with the same \(m\) and \(\alpha\), as the cutter’s addendum would need to extend into a region where the gear tooth does not exist. The table below summarizes the parameter changes for a highly positively shifted internal strain wave gear spline compared to a standard one.
| Parameter | Standard Internal Gear (\(\xi=0\)) | Positively Shifted Strain Wave Gear Spline (\(\xi \gg 0\)) |
|---|---|---|
| Pitch Diameter \(d_f\) | \(m \cdot z\) | \(m \cdot z\) (unchanged reference) |
| Minor (Tip) Diameter \(d_a\) | \(d_f – 2h_a\) | \(d_f + 2|h_a|\) (becomes > \(d_f\)) |
| Major (Root) Diameter \(d_i\) | \(d_f + 2h_f\) | \(d_f + 2h_f + \text{shift effect}\) |
| Pitch Circle Tooth Thickness \(S\) | \(\pi m / 2\) | \(\pi m / 2 – 2m \xi \tan \alpha\) (can be negative) |
| Location of Pitch Circle | Within tooth height | May be below tooth tip (virtual) |
This geometric anomaly is the fundamental reason why traditional shaper cutter design fails. The traditional method assumes the cutter’s reference pitch circle meshes with the gear’s pitch circle. If that gear pitch circle is not a physically meaningful location within the tooth profile, the cutter design parameters become undefined or impractical.
The solution I employ hinges on a fundamental property of involute gears: the base pitch \(P_b\) is invariant and must be identical for two mating gears (or a gear and its generating tool). The base pitch is given by:
$$ P_b = \pi m \cos \alpha $$
This invariance allows for the concept of “variable module and variable pressure angle.” On any concentric circle of diameter \(d_y\) on the gear, we can define a local pressure angle \(\alpha_y\). The relationship between the radii and pressure angles is \(r_b = r_y \cos \alpha_y = r_f \cos \alpha\). From this, we can define an equivalent or “design” module \(m_y\) for that specific circle such that the base pitch remains constant:
$$ \pi m \cos \alpha = \pi m_y \cos \alpha_y $$
$$ m_y = m \frac{\cos \alpha}{\cos \alpha_y} $$
Furthermore, the diameter \(d_y\) of this chosen circle is related to the design module by \(d_y = m_y \cdot z\). The key insight is that we can abandon the original, geometologically problematic pitch circle (\(d_f, \alpha\)) and select a new, more appropriate reference circle somewhere between the gear’s major and minor diameters where a valid meshing condition with a shaper cutter can be established. This selected circle, with parameters (\(d_y, \alpha_y, m_y\)), becomes the new reference for designing the shaper cutter. The tooth thickness \(S_y\) on this new reference circle must be calculated. The general formula for tooth thickness on an arbitrary diameter \(d_y\) for a profile-shifted gear is:
$$ S_y = d_y \left[ \frac{S}{d_f} + \text{inv}(\alpha) – \text{inv}(\alpha_y) \right] $$
Substituting \(S = \frac{\pi m}{2} – 2m \xi \tan \alpha\) for an internal gear, we get:
$$ S_y = d_y \left[ \frac{\pi m – 2\pi m \xi \tan \alpha / \pi}{d_f} + \text{inv}(\alpha) – \text{inv}(\alpha_y) \right] = d_y \left[ \frac{\pi m – 4m \xi \tan \alpha}{2d_f} + \text{inv}(\alpha) – \text{inv}(\alpha_y) \right] $$
A more compact form often used is:
$$ S_y = \pi m_y – \left[ \frac{d_y}{d_f} (\pi m – S) – d_y (\text{inv}(\alpha_y) – \text{inv}(\alpha)) \right] $$
With \(m_y\), \(\alpha_y\), \(d_y\), and \(S_y\) determined for the gear, we can now design the shaper cutter. The cutter will be designed as if it were to mesh with a “virtual gear” defined by these new parameters. Therefore, the cutter’s nominal module and pressure angle are set equal to \(m_y\) and \(\alpha_y\), respectively. A shaper cutter has a series of cross-sections along its axis, each with a different effective profile shift due to the back taper (relief angles). The section where the shift is zero is called the “original section” and serves as the design datum. In this original section, the cutter’s pitch circle tooth thickness \(S_c\) must equal the space width on the reference circle of the virtual gear:
$$ S_c = P_y – S_y = \pi m_y – S_y $$
The addendum \(h_{a,c}\) and dedendum \(h_{f,c}\) of the cutter in the original section are determined by the gear’s corresponding dimensions relative to the new reference circle \(d_y\). For an internal gear, the cutter’s addendum corresponds to the gear’s dedendum measured from \(d_y\), and the cutter’s dedendum corresponds to the gear’s addendum from \(d_y\), plus a clearance \(c m_y\):
$$ h_{a,c} = \frac{d_i – d_y}{2} $$
$$ h_{f,c} = \frac{d_y – d_a}{2} + c m_y $$
where \(c\) is the clearance coefficient, typically between 0.25 and 0.35. The number of teeth on the shaper cutter \(z_c\) is chosen based on structural and functional considerations, often between 80 and 120 for small module tools to ensure sufficient chip space and strength. Other parameters, such as rake angle, relief angles, and tolerances, are designed according to standard practices for precision gear cutting tools.
To illustrate this methodology, I will walk through a detailed application example for a typical small module strain wave gear component. The given parameters of the internal steel wheel (circular spline) are as follows:
| Parameter | Symbol | Value |
|---|---|---|
| Normal Module | \(m\) | 0.25 mm |
| Normal Pressure Angle | \(\alpha\) | 20° |
| Number of Teeth | \(z\) | 160 |
| Minor (Tip) Diameter | \(d_a\) | 41.58 mm |
| Major (Root) Diameter | \(d_i\) | 42.48 mm |
| Ball (Pin) Measurement Over | \(M\) | 41.44 mm |
| Ball Diameter | \(d_{ball}\) | 0.433 mm |
First, we verify the problematic condition. The pitch diameter is \(d_f = m \cdot z = 0.25 \times 160 = 40.00 \text{ mm}\). Clearly, \(d_a = 41.58 \text{ mm} > d_f = 40.00 \text{ mm}\). The pitch circle lies 0.79 mm below the tooth tip. Using the formula for ball measurement for an internal gear, the effective tooth thickness on the pitch circle can be derived. The calculation yields a value of approximately \(S \approx -0.462 \text{ mm}\). A negative tooth thickness on the pitch circle confirms the pitch circle is in the tooth space, not on the tooth material, and the shift coefficient calculated from \(S = \frac{\pi m}{2} – 2m \xi \tan \alpha\) is:
$$ \xi = \frac{\frac{\pi m}{2} – S}{2m \tan \alpha} = \frac{\frac{\pi \times 0.25}{2} – (-0.462)}{2 \times 0.25 \times \tan 20^\circ} \approx \frac{0.3927 + 0.462}{0.18198} \approx \frac{0.8547}{0.18198} \approx 4.697 $$
This large positive shift coefficient is characteristic of strain wave gear design to accommodate the deformation of the flexspline and ensure proper conjugate action.
Since conventional design is impossible, I apply the variable module/pressure angle method. I must select a suitable reference circle diameter \(d_y\). A logical choice is a diameter somewhere near the middle of the active tooth profile, for instance, closer to the ball measurement diameter. However, for calculation stability, I often select a design pressure angle \(\alpha_y\) first. Choosing a larger pressure angle increases the design module \(m_y\) via \(m_y = m \cos \alpha / \cos \alpha_y\), which can lead to more favorable cutter dimensions. Let us select \(\alpha_y = 26^\circ\).
$$ m_y = m \frac{\cos \alpha}{\cos \alpha_y} = 0.25 \times \frac{\cos 20^\circ}{\cos 26^\circ} = 0.25 \times \frac{0.9396926}{0.898794} \approx 0.261376 \text{ mm} $$
The corresponding reference circle diameter is:
$$ d_y = m_y \cdot z = 0.261376 \times 160 = 41.82016 \text{ mm} $$
This diameter lies between \(d_i = 42.48 \text{ mm}\) and \(d_a = 41.58 \text{ mm}\), which is valid. Next, I calculate the tooth thickness \(S_y\) on this new reference circle. Using the formula:
$$ S_y = \pi m_y – \left[ \frac{d_y}{d_f} (\pi m – S) – d_y (\text{inv}(\alpha_y) – \text{inv}(\alpha)) \right] $$
We have \(\text{inv}(\alpha) = \text{inv}(20^\circ) \approx 0.0149044\), \(\text{inv}(\alpha_y) = \text{inv}(26^\circ) \approx 0.0344765\), and \(\pi m – S = \pi \times 0.25 – (-0.462) \approx 0.785398 + 0.462 = 1.247398\).
$$ S_y = \pi \times 0.261376 – \left[ \frac{41.82016}{40.00} \times 1.247398 – 41.82016 \times (0.0344765 – 0.0149044) \right] $$
$$ S_y \approx 0.82101 – \left[ 1.04504 \times 1.247398 – 41.82016 \times 0.0195721 \right] $$
$$ S_y \approx 0.82101 – \left[ 1.3038 – 0.81832 \right] $$
$$ S_y \approx 0.82101 – 0.48548 \approx 0.33553 \text{ mm} $$
Now, I proceed to design the shaper cutter for this strain wave gear spline. The cutter’s basic parameters in its original section are:
- Module: \(m_c = m_y = 0.261376 \text{ mm}\)
- Pressure Angle: \(\alpha_c = \alpha_y = 26^\circ\)
- Number of Teeth: I select \(z_c = 100\) (a common value for tool rigidity and chip control).
- Pitch Circle Tooth Thickness: \(S_c = \pi m_y – S_y \approx 0.82101 – 0.33553 = 0.48548 \text{ mm}\).
- Addendum: \(h_{a,c} = (d_i – d_y)/2 = (42.48 – 41.82016)/2 \approx 0.32992 \text{ mm}\).
- Dedendum: Using a clearance coefficient \(c = 0.25\), \(h_{f,c} = (d_y – d_a)/2 + c m_y = (41.82016 – 41.58)/2 + 0.25 \times 0.261376 \approx 0.12008 + 0.065344 \approx 0.18542 \text{ mm}\).
- Tip Diameter of Cutter: \(d_{a,c} = m_c z_c + 2 h_{a,c} = 0.261376 \times 100 + 2 \times 0.32992 \approx 26.1376 + 0.65984 \approx 26.79744 \text{ mm}\).
- Root Diameter of Cutter: \(d_{f,c} = m_c z_c – 2 h_{f,c} \approx 26.1376 – 2 \times 0.18542 \approx 26.1376 – 0.37084 \approx 25.76676 \text{ mm}\).
The full design involves additional specifications: a positive rake angle (e.g., \(5^\circ\)), primary and secondary relief angles, tolerances on tooth thickness and runout, and material specification (typically high-speed steel or powder metallurgy steel for such small modules). The cutter would be of the shell or shank type, suitable for mounting on a precision gear shaper machine. The following table consolidates the key design parameters for the shaper cutter tailored for this specific strain wave gear application.
| Cutter Parameter | Symbol | Value | Note |
|---|---|---|---|
| Design Module | \(m_c\) | 0.261376 mm | Derived from variable module method |
| Design Pressure Angle | \(\alpha_c\) | 26° | Selected reference pressure angle |
| Number of Teeth | \(z_c\) | 100 | Chosen for tool design |
| Reference Pitch Diameter | \(d_{p,c}\) | \(m_c z_c = 26.1376\) mm | Cutter’s pitch circle |
| Tooth Thickness on \(d_{p,c}\) | \(S_c\) | 0.48548 mm | Equals space width on gear’s \(d_y\) |
| Addendum | \(h_{a,c}\) | 0.32992 mm | From gear’s dedendum relative to \(d_y\) |
| Dedendum | \(h_{f,c}\) | 0.18542 mm | From gear’s addendum plus clearance |
| Tip Diameter | \(d_{a,c}\) | ~26.797 mm | |
| Root Diameter | \(d_{f,c}\) | ~25.767 mm | |
| Rake Angle (Face) | \(\gamma\) | 5° (example) | For cutting efficiency |
| Primary Relief Angle | \(\alpha_r\) | 3°-4° (example) | For side cutting edges |
The successful application of this cutter in production validates the variable module and pressure angle approach. It underscores a critical principle in the design of tools for advanced gear systems like the strain wave gear: when the standard kinematic relationships break down due to extreme geometric conditions, one must return to the fundamental, invariant laws of gearing—in this case, the constancy of the base pitch—to establish a new, valid reference framework for tool design.
In conclusion, the design of shaper cutters for small module, highly positively shifted involute strain wave gears presents a significant technical challenge that cannot be met with conventional methodologies. The condition where the internal spline’s minor diameter exceeds its pitch diameter is a direct consequence of the large positive shift coefficients required for optimal performance of the strain wave gear mechanism. The method I have detailed, based on the principle of variable module and variable pressure angle, provides a robust and theoretically sound solution. By selecting an appropriate new reference circle on the gear tooth profile where a valid meshing condition exists, and ensuring the base pitch equality is maintained, we can derive a consistent set of parameters for the shaper cutter. This approach ensures the accurate generation of the complex tooth forms essential for the reliable and efficient operation of strain wave gear systems in demanding applications such as aerospace actuators, robotic joints, and precision optical devices. As strain wave gear technology continues to evolve towards even higher precision and miniaturization, such advanced tool design techniques will remain indispensable for their manufacture.
