In the formula, although the meanings of R2 (T) cos α inside and outside the brackets are different, the results are the same. If rb2rb22 = R2 (T) cos α, the dynamic model of minus variable speed integrated gear is shown in the figure. The small cylindrical gear and the non-circular gear are equivalent to the moment of inertia with the radius of gyration RB1 and Rb2 respectively, the tooth is equivalent to spring and damping, the meshing stiffness is km, the meshing damping is cm, e (T) is the static transmission error of the teeth, the active torque acting on the small cylindrical gear is T1, and the resistance torque on the non-circular gear is T2.

Then the two degree of freedom dynamic equation of non-circular gear is as follows:
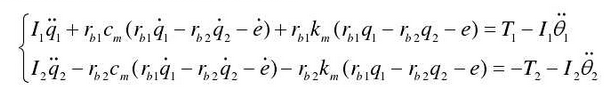
Considering that the value of elastic angle of gear is very small, the following assumptions are made:
(1) The elastic rotation angle has no effect on the instantaneous radial diameter of noncircular gear, and the radial diameter R is a function of time t;
(2) When the gear rotates elastically, the direction of normal force between teeth remains unchanged.
Assuming that the angular velocity of the small cylindrical gear is the same as that of the motor, which is a known function (constant value or change with time), then the elastic deformation of the meshing teeth between the cylindrical gear and the non-circular gear is converted into the elastic angle Q2 of the non-circular gear, then the small cylindrical gear has no elastic angle. By substituting Q1 = 0 into the formula, the dynamic vibration equation of single degree of freedom gear with non-circular gear elastic angle Q2 as independent variable is obtained
Taking the typical elliptic gear ratio as the transmission ratio IB of the reducer variable speed integrated gear, the total transmission ratio function i12 of the reducer variable speed integrated gear is as follows:

