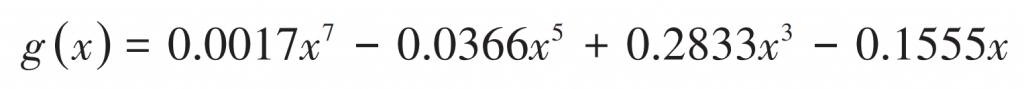Generally speaking, the coincidence degree of a helical gear system is greater than 2, and the continuous gradual involution of its meshing process makes the meshing process of the helical gear more smooth than that of a spur gear system. However, using the segmented clearance function g (x), the analysis results deviate greatly from engineering practice. Therefore, it is necessary to polynomial fit the clearance function g (x). The table provides the coefficients corresponding to polynomial fitting at different orders.
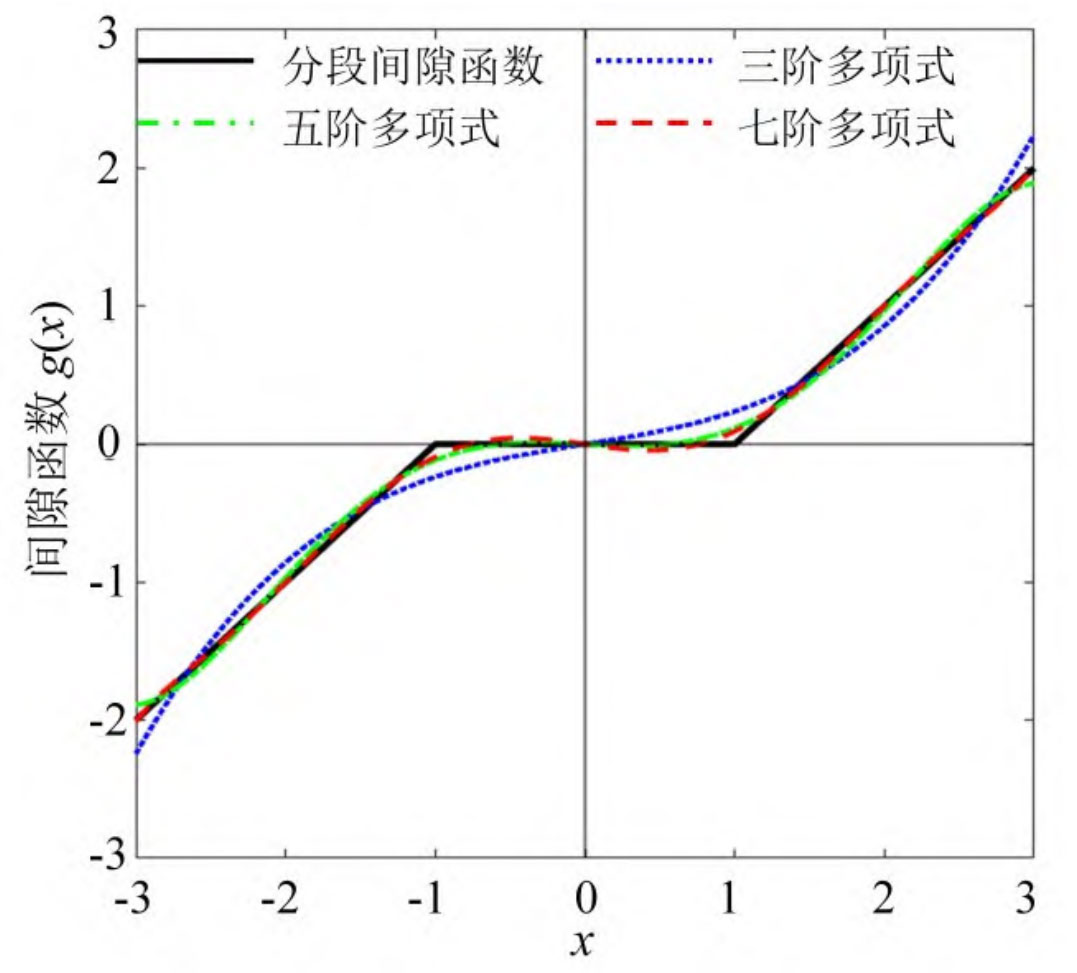
The figure shows the initial piecewise linear function g (x) and its polynomial fitting curve of each order. It can be seen that as the fitting order increases, the deviation gradually decreases.
| Polynomial term | 3rd-order | 5th-order | 7th-order |
| x | 0.173 86 | -0.052 678 | -0.155 49 |
| x^3 | 0.063 75 | 0.180 83 | 0.283 3 |
| x^5 | — | -0.011 69 | -0.036 636 |
| x^7 | — | — | 0.001 711 7 |
Taking into account both computational efficiency and accuracy, a 7-order polynomial is used to represent the tooth side clearance function g (x):