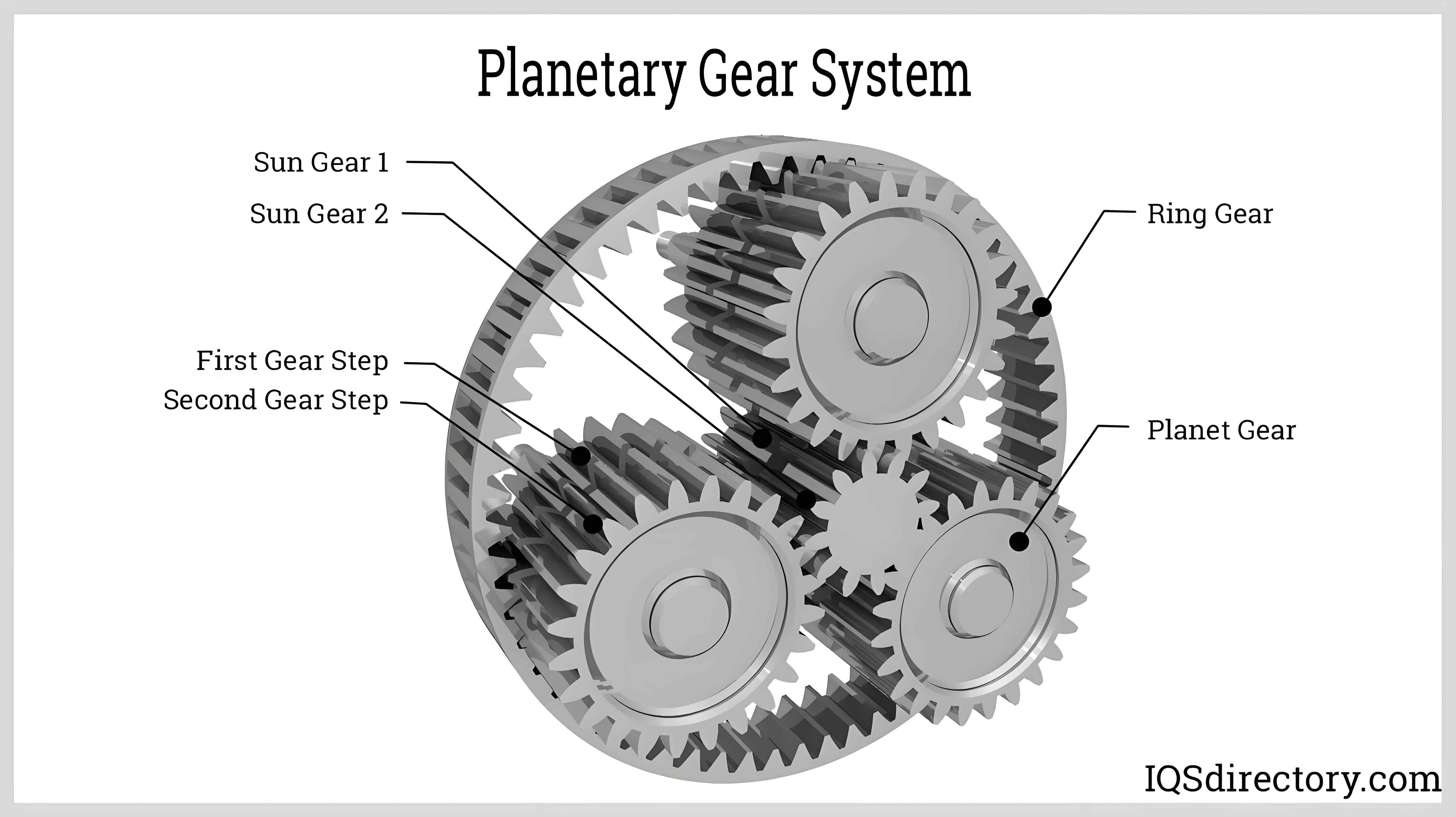
This study investigates the dynamic characteristics of linear-conjugate planet gear systems with small tooth differences through mathematical modeling, simulation, and experimental validation. The system’s unique meshing mechanism enables high torque density while maintaining compact dimensions – a critical requirement for advanced planetary gear applications.
Mathematical Formulation
The coordinate system for external gear tooth profile generation is established as shown below:
The external gear profile comprises three linear segments with distinct geometric relationships:
$$b = r_1\left(\cos\frac{\theta}{2} + \sin\frac{\theta}{2}\cot\beta\right)$$
$$k = -\cot\beta$$
$$x_a = \frac{r_1\theta}{2}\cos\alpha$$
The complete tooth profile equation for external gears becomes:
$$R_{1p} = \left[x_{oa}, x_{ab}, x_{bc}\right]^T = f(r_1, \beta, \theta)$$
For internal gear generation using conjugate theory:
$$R_{2i} = M_{21}(\phi_1,\phi_2)R_{1p} + E(\phi_1)$$
$$v_{1p}^{rel} \cdot n_1 = 0$$
Where the coordinate transformation matrix contains critical planetary gear relationships:
$$M_{21} = \begin{bmatrix}
\cos\Delta\phi & -\sin\Delta\phi & (r_2-r_1)\sin\phi_2 \\
\sin\Delta\phi & \cos\Delta\phi & (r_1-r_2)\cos\phi_2 \\
0 & 0 & 1
\end{bmatrix}$$
Dynamic Simulation Results
Planet gear meshing forces under various operating conditions reveal distinct dynamic behaviors:
| Condition | Speed (rpm) | Torque (N·m) | Peak Force (N) | RMS (N) |
|---|---|---|---|---|
| Case 1 | 600 | 80 | 1,453.54 | 1,219.86 |
| Case 2 | 1,400 | 80 | 1,492.75 | 1,214.07 |
| Case 3 | 2,200 | 80 | 1,628.77 | 1,208.66 |
| Case 4 | 1,400 | 40 | 912.66 | 606.18 |
| Case 5 | 1,400 | 120 | 2,139.88 | 1,849.17 |
The meshing force error between simulation and theoretical calculations remains below 7.01%, confirming model accuracy. The planet gear system demonstrates speed-dependent vibration characteristics:
$$a_{vib} = 0.0183\omega + 0.0024T + 0.1276$$
Where ω represents input speed (rad/s) and T denotes load torque (N·m).
Experimental Validation
Vibration testing using IEPE accelerometers shows strong correlation with simulation results:
| Condition | Simulated RMS (m/s²) | Experimental RMS (m/s²) | Error (%) |
|---|---|---|---|
| 600 rpm/80 N·m | 0.296 | 0.269 | 9.12 |
| 1,400 rpm/80 N·m | 0.879 | 0.818 | 6.94 |
| 2,200 rpm/80 N·m | 1.693 | 1.537 | 9.21 |
Frequency domain analysis reveals planet gear meshing characteristics:
$$f_m = \frac{z\omega}{60} \pm \Delta f_e$$
Where z represents tooth count and Δfe accounts for eccentricity effects (typically 60-80 Hz).
Conclusion
This comprehensive investigation establishes that linear-conjugate planet gear systems exhibit predictable dynamic behavior with vibration characteristics directly correlated to operational parameters. The maximum 9.21% deviation between simulation and experimental results validates the mathematical models, providing critical insights for optimizing planet gear configurations in high-precision transmission systems.
